«Современный мир быстро меняется, темпы нарастают, поэтому человеку очень важно научиться учиться самому, приобретать новые знания и совершать открытия на стыке знаний, на стыке наук и дисциплин, а для того, чтобы иметь такой навык, нужно иметь фундаментальную базу основных знаний, так как современные достижения делаются с использованием больших данных и математических вычислений», – сказал Президент Российской Федерации В. В. Путин на Всероссийском открытом уроке в режиме видеоконференции [1].
Образование как один из видов обучения детей в нашей стране сталкивается с глобальными конкурентами [1]. Самым серьезным соревнованием в XXI веке является то, как ученик сможет применить знания и умения, полученные на уроке, в реальной жизни [2]. Знания и умения – это математическая грамотность [2]. Способность к математической грамотности – это способность определять, понимать и использовать математические знания для удовлетворения индивидуальных жизненных потребностей [4]. Трудность, которая чаще всего возникает у школьников, заключается в формулировании задач для повседневной жизни, поскольку школьник еще не умеет пользоваться этими способностями [6]. Это приводит к тому, что способности, которые должны быть понятны учащимся, застревают, и они сталкиваются с трудностями при поиске и использовании своих способностей [7]. Оценка уровня грамотности для каждого ученика может быть одинаковой, но при представлении успеваемости каждый ученик имеет свои особенности, поэтому для измерения и определения уровня успеваемости ученика необходим уровень достижений [4]. Представление результатов математической грамотности учащихся может быть легким и трудным, поскольку для этого необходим уровень достижений и серфинг по характеристикам самого учащегося.
В настоящее время многие процессы жизни человека автоматизируются с помощью компьютеров и компьютерных программ. В областях промышленности, бизнеса, экономики и образования используют информационные системы. Труд человека все чаще заменяется работой машин. В будущем эта тенденция будет только расти. Вместе с тем будет увеличиваться и потребность в специалистах в сфере компьютерных программ. Поэтому, большинству людей (специалистов) необходимо идти в ногу со временем, приобретать навыки в области программирования. Даже несмотря на то, что он не является их основным видом деятельности. Вышесказанное ставит перед рядовым служащим ряд качественно новых задач.
Алгоритмическое мышление формируется в результате многократного решения специально подготовленных задач, которые опираются на базовые понятия программирования, такие как математические операции, переменные, алгоритмы и структуры данных. Помочь в этом могут специальные порталы для обучения с использованием автоматических проверяющих систем. Они включают в себя наборы задач на проверку различных алгоритмических навыков и понимания тонкостей языков программирования.
Линейное программирование возникло как один из разделов теории оптимизации. Применения методов линейного программирования является важным направлением улучшения планирования и анализа деятельности предприятия. Математические модели позволяют конкретизировать информацию, создавать и моделировать варианты, выбирать оптимальные решения. Современные условия диктуют необходимость применения новых инструментов анализа работы компаний. Задачи линейного программирования возникают в ежедневной деятельности логистических, торговых, распределительных фирм и организаций.
Вот несколько стратегий, которые педагоги могут использовать для обучения старших школьников линейному программированию:
1. Сделать пример понятным
Отличным способом представить линейное программирование является предоставление понятного сценария, с которым школьники легко могут сопоставиться. Например, использование проблемы бюджетирования для иллюстрации того, как линейное программирование может использоваться для наиболее эффективного распределения ограниченных ресурсов.
2. Использование визуальных средств
Линейное программирование включает использование графиков и диаграмм – визуального представления задачи оптимизации. Поэтому педагоги должны использовать визуальные средства, такие как графики и диаграммы, чтобы помочь школьникам лучше понять концепцию.
3. Начать с простых моделей
Важно начать с простых моделей линейного программирования, прежде чем перейти к более сложным. Начиная с простых моделей, школьники могут чувствовать себя менее запуганными, что помогает повысить их уверенность в изучаемой теме.
4. Активное участие
Чтобы стимулировать активное участие, преподаватели могут использовать коллективные занятия, такие как групповые обсуждения, проекты и задачи по решению проблем. Создавая среду сотрудничества и активного участия, школьники вероятнее будут заинтересованы и будут учиться больше.
5. Предоставление примеров из реальной жизни
Помимо теоретических концепций, педагогам следует предоставлять примеры из реальной жизни о том, как линейное программирование используется в промышленности и бизнесе. Такие примеры помогают школьникам увидеть актуальность концепции и ее применимость для решения сложных задач оптимизации.
6. Развитие математических навыков
Линейное программирование включает математические уравнения и концепции. Поэтому для обучения в старших классах линейному программированию педагоги должны убедиться, что у школьников есть необходимые математические навыки, необходимые для решения задач оптимизации. Крайне важно поэтапно объяснить необходимые алгебраические уравнения. Практика решения задач является отличным способом закрепления понимания основных концепций.
7. Поощрение исследования и экспериментирования
Наконец, чтобы поддерживать энтузиазм, преподаватели могут предоставлять задания, которые поощряют исследование и экспериментирование с различными моделями. Эти проекты помогут школьникам понять, как моделируются проблемы реального мира и какие факторы влияют на их результаты.
Рассмотрим методику обучения учащихся решению задач линейного программирования в различных школьных учебниках. Под задачей линейного программирования в школьном курсе информатики понимается линейная функция с заданными линейными ограничениями, которую нужно максимизировать или минимизировать. В учебнике И.Г. Семакина за 10-11 класс (базовый уровень) содержательная линия «Формализация и моделирование» рассматривается в главе 6 «Технологии информационного моделирования». В результате анализа главы в рамках рассматриваемой темы можно сделать вывод, что математическое моделирование изучается в рамках его компьютерной реализации, а в ходе постепенно расширяются математические знания и навыки учащихся. Также рассматриваются элементы математической статистики и моделирование корреляционных зависимостей, основные задачи оптимизации, решение которых представляется в электронной таблице MS Excel. После изучения темы в учебнике предлагается система основных понятий, список вопросов с целью проверки уровня теоретических знаний учащихся, индивидуальные задания. В учебнике Н.Д. Угриновича для 11 класса (профильный уровень) ЗЛИ рассматриваются в главе 1 «Построение и исследование информационных моделей». Анализ этой главы показал, что представленные в ней задачи относятся к различным предметным областям (физика, экономика, химия и т.д.). Задачи решаются с помощью сред программирования Visual Basic и Turbo Delphi, а также в электронной таблице MS Excel (надстройка «Поиск решения», «Подбор параметра»). Таким образом, изучение данной темы начинается с изложения теоретических основ оптимизационного моделирования (формальная модель, критерий оптимальности, целевая функция, линейное программирование, максимум и минимум целевой функции и др.). Далее рассматривается построение и исследование различных оптимизационных моделях на языках Visual Basic и Turbo Delphi. В заключении каждого параграфа рассматривается компьютерная модель в электронных таблицах.
Мы провели со школьниками проектную работу, которая была посвящена разработке программы в среде Delphi, реализующую решения ЗЛП симплекс-методом и графическим методом. Симплекс-метод является методом целенаправленного перебора опорных решений задачи и позволяет за конечное число шагов либо найти оптимальное решение, либо установить, что оптимальное решение отсутствует. Суть графического метода в следующем: каждое из заданных ограничений ЗЛП определяет на координатной плоскости некоторую полуплоскость, а система неравенств в целом – пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений.
Программа вычисляет значения целевой функции и значения входных переменных при условии максимизации (минимизации) значения. На главной форме расположено меню: файл (новый, открыть, сохранить, сохранить как, руководство пользователя, выход), правка (изменить функцию, добавить ограничения, удалить ограничения, очистить), вычисления (симплекс-метод, графический метод, параметры задачи).
В начале работы приложения нужно или открыть уже созданный файл с условием ЗЛП (*.tsk), или создать новый. Если данные введены не корректно, то с помощью категории Правка можно изменить функцию или ограничения.
После ввода данных выбрать Вычисления – Симплекс-метод (рис. 1).
Рис. 1. Решение ЗЛП
Для решения задач графическим методом вначале работы программы нужно ввести количество заданных ограничений (не более 15). Затем нужно вести данные, т.е. значения целевой функции. Если не все данные будут введены, то при нажатии на кнопку «Графический метод». Если же все данные введены корректно, то в поле linage 1 (рис. 2) нарисуются графики ограничений и целевой функции заданной ЗЛП. Внизу окна приложения (StatusBarl) выведется ответ.
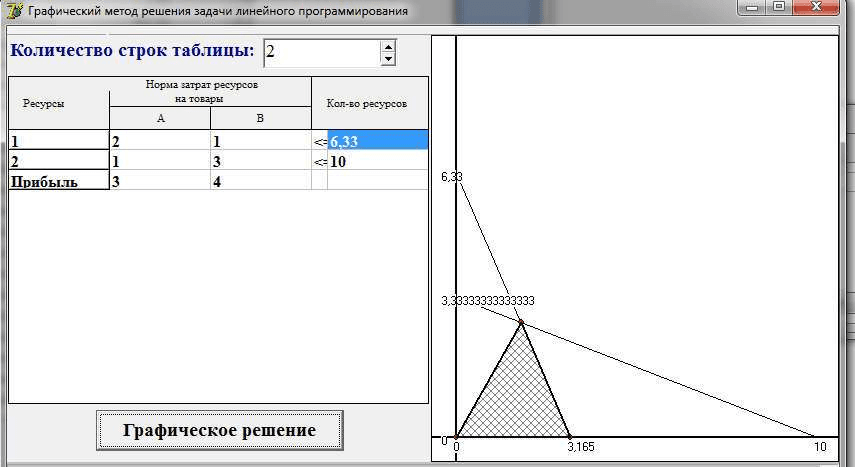
Рис. 2. Решение ЗЛП графическим методом
Таким образом, программа вычисляет значения целевой функции и значения входных переменных при условии максимизации (минимизации) значения.
Наш опыт показывает, что написание программного кода для решения таких задач не только доступно школьникам, но и вызывает у них дополнительный интерес к изучению данной проблемы. Разработанное приложение применяется нами на уроках информатики при решении ЗЛП с целью проверки полученного решения в MS Excel.
В заключение преподавание школьникам линейного программирования с использованием вышеуказанных стратегий может сделать концепцию понятной и увлекательной. Позволяя школьникам понять методологию линейного программирования, они будут более уверены в своей способности решать задачи линейного программирования и станут лучшими математическими решателями проблем.
Не стоит забывать о практической направленности курса. Линейное программирование призвано решать реальные прикладные задачи, помогая осмыслить роль математических дисциплин в окружающем мире. Показано, что линейное программирование тесно связано с такими смежными дисциплинами как информатика, линейная алгебра, математическое программирование, теория оптимального управления, организация производства.

.png&w=640&q=75)