Хорошо известно [1, 2], что неявные разностные схемы для одномерного параболического уравнения безусловно устойчивы. Попытки обобщить их на многомерный случай сталкиваются с большими трудностями. Для начально-краевой задачи
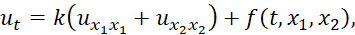 (1)
(1)
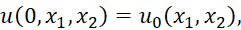 (2)
(2)
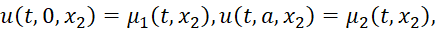 (3)
(3)
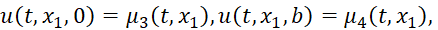 (4)
(4)
при использовании неявной разностной схемы число операций оцениваются величиной ~N3p-1.
Здесь – 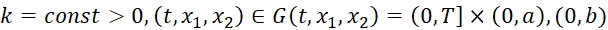 ,
,
p – число пространственных переменных.
Отсюда следует, что если для одномерного уравнения теплопроводности явная схема (условно устойчивый) является невыгодной при использовании неявных разностных схем (безусловно устойчивый), то в многомерном случае (p>2) неявные разностные схемы становятся невыгодными (в плане экономности, т.е. время счета, количество итераций, объём занимаемой алгоритмом памяти и т.п.) по сравнению с явной разностной схемой.
Несмотря на эти трудности, для многомерного уравнения теплопроводности построены абсолютно устойчивые разностные схемы, которые позволяют вести счет с шагом τ~h [3, 4]. Для таких разностных схем приблизительное количество операций, требуемых для перехода со слоя на слой равно ~Np. Это означает, что число действий в расчете на узел пространственной сетки не зависит от шагов hα, α=1,…,p, где hα – шаги по пространственным переменным. Такие схемы называются экономичными разностными схемами.
Мы будем рассматривать один из таких экономичных разностных схем для многомерного уравнения теплопроводности. Оно называется схемой переменных направлений. Ниже приведен шаблон схемы переменных направлений, в которую введен полуцелый слой 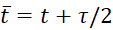 .
.
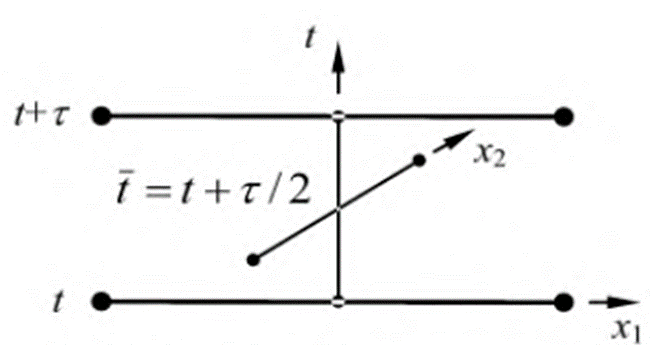
Рис. Шаблон разностной схемы
Составим согласно этому шаблону следующую разностную схему
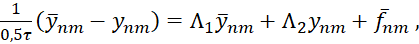 (5)
(5)
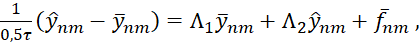 (6)
(6)
Λ1, Λ2 определены следующим образом
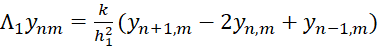 , (7)
, (7)
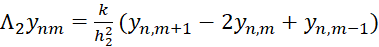 , (8)
, (8)
а 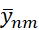 берется на полуцелом слое
берется на полуцелом слое 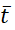 .
.
Вычислительная процедура по схеме (5), (6) складывается из перехода со слоя t на слой 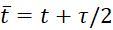 согласно уравнению (5) и далее переход со слоя
согласно уравнению (5) и далее переход со слоя 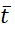 на слой t+τ согласно уравнению (6). На первом шаге неизвестными выступают величины
на слой t+τ согласно уравнению (6). На первом шаге неизвестными выступают величины 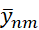 с полуцелого слоя, они находятся методом прогонки по направлению x1 путем обращения разностного оператора Λ1, который согласно (8) определен на трехточечном шаблоне. На втором шаге при переходе на слой t+τ неизвестными выступают
с полуцелого слоя, они находятся методом прогонки по направлению x1 путем обращения разностного оператора Λ1, который согласно (8) определен на трехточечном шаблоне. На втором шаге при переходе на слой t+τ неизвестными выступают 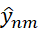 , они находятся прогонкой, но в поперечном x2 направлении путем обращения оператора Λ2, который также определен на трехточечном шаблоне. При этом, и для первой, и для второй прогоник имеется диагональное преобладание, так что прогонки устойчивы, а разностное решение существует и единственно.
, они находятся прогонкой, но в поперечном x2 направлении путем обращения оператора Λ2, который также определен на трехточечном шаблоне. При этом, и для первой, и для второй прогоник имеется диагональное преобладание, так что прогонки устойчивы, а разностное решение существует и единственно.
Устойчивость продольно-поперечной схемы можно исследовать методом разделения переменных. Для этого положим
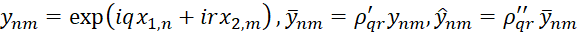 , (9)
, (9)
где 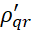 ,
, 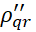 – множители роста гармоник на первом и втором полушагах. Подставляя представления (9) в (5), (6), находим
– множители роста гармоник на первом и втором полушагах. Подставляя представления (9) в (5), (6), находим
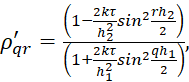 (10)
(10)
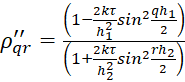 . (11)
. (11)
Учитывая (10), (11), можно убедиться, что для любых гармоник и при любых шагах сетки верно неравенство 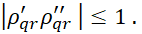 Таким образом, при переходе со слоя на слой ошибки в начальных данных не растут и разностная схема (5), (6) равномерно и безусловно устойчива по начальным данным. Можно также проверить, что дополнительный признак устойчивости по правой части выполняется на каждом из полушагов по времени, т.е. разностная схема (5), (6) также устойчива по правой части.
Таким образом, при переходе со слоя на слой ошибки в начальных данных не растут и разностная схема (5), (6) равномерно и безусловно устойчива по начальным данным. Можно также проверить, что дополнительный признак устойчивости по правой части выполняется на каждом из полушагов по времени, т.е. разностная схема (5), (6) также устойчива по правой части.
Теперь выясним, какой порядок аппроксимации имеет рассматриваемая нами разностная схема. Для этого вычтем из уравнения (5) уравнение (6), тогда получим
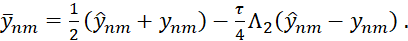 (12)
(12)
Складывая уравнения (5), (6) и подставляя в них выражения (12), получим
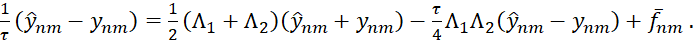 (13)
(13)
Предпоследний член в правой части (13), после разложения в ряд Тейлора, может быть аппроксимирован выражением 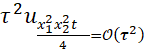 . Остальные члены в (13) совпадают с симметричным вариантом схемы, которая имеет порядок аппроксимации
. Остальные члены в (13) совпадают с симметричным вариантом схемы, которая имеет порядок аппроксимации 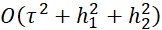 . Тем самым, продольно-поперечная схема имеет второй порядок точности по всем переменным.
. Тем самым, продольно-поперечная схема имеет второй порядок точности по всем переменным.
Теперь займемся с аппроксимацией граничных условий (3), (4) для продольно-поперечной схемы. При решении уравнения (6) относительно 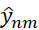 необходимо использовать граничное условие на сторонах прямоугольника x2=0 и x2=b. В этом случае можно положить, что
необходимо использовать граничное условие на сторонах прямоугольника x2=0 и x2=b. В этом случае можно положить, что
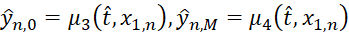 . (14)
. (14)
При решении уравнения (5) относительно 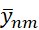 необходимы граничные условия на сторонах x1=0 и x1=a. Для их получения необходимо воспользоваться уравнением (12), тогда имеем
необходимы граничные условия на сторонах x1=0 и x1=a. Для их получения необходимо воспользоваться уравнением (12), тогда имеем
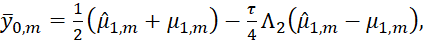 (15)
(15)
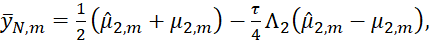 (16)
(16)
где m=1,…, M-1. Эти граничные условия обеспечивают погрешность аппроксимации 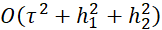 .
.
Проведенное исследование аппроксимации и устойчивости показывает, что схема (5), (6) безусловно сходится в норме 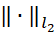 , при этом в прямоугольной области на равномерной сетке и при граничных условиях (15), (16) разностная схема имеет точность
, при этом в прямоугольной области на равномерной сетке и при граничных условиях (15), (16) разностная схема имеет точность 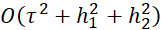 на решениях с непрерывными пятыми производными.
на решениях с непрерывными пятыми производными.

.png&w=640&q=75)