Основы динамики как современная проблема классической физики

Понятие «количество движения» сформировалось в недрах теории импетуса, которая описывала движение тел тяжелея воздуха или воды, как стремление к покою на поверхности Земли, в которой сконцентрирован центр мироздания. В науке античности движение тела к месту его покоя называлось «естественным движением». В противном случае движение называлось «насильственным». Аристотель полагал, что «насильственное движение» возможно только в том случае, если к телу приложена сила со стороны другого тела:

«Все движущееся необходимо приводить в движение чем-нибудь. Если оно в самом себе не имеет начала движения, то ясно, что оно приводится в движение другим (тогда движущим будет иное)» [1, т.3, с. 205].

Скорость движущегося тела Аристотель считал пропорциональной приложенной силе. Таким образом, Аристотель понимал движение, как следствие действия некой внешней силы, при этом рассматривал скорость этого движения пропорционально величине этой силы.

Итак, понятие силы, как физической реальности введено в оборот Аристотелем, он же связывает две физические величины силу и скорость прямой пропорциональностью. Фактически, это стало основой для понимания «количества движения». Тут важно отметить, что природой движения Аристотель рассматривает именно силу, а не импульс /1/.

Разница между этим двумя понятиями принципиальная.

Сила, это постоянное во времени явление, и может не изменяться неограниченно долго, в то время как импульс, это отношение действующей силы ко времени, в течение которого эта сила действует на тело. Если сила пропорциональна скорости, то импульс пропорционален ускорению (изменению скорости во времени), при этом, при начальной скорости равной нулю, начальная сила движения также равна нулю, а вот конечная по своему модулю равна величине механического импульса, если движение связано с внешним импульсом.

Так могла бы развиваться классическая механика, если бы не произошло отождествление движения свободного падания с понятием силы, принуждающей тело к движению. Эта ошибка и требует сегодня своего устранения из классической физики.

Идею принудительного движения Аристотеля развил теолог Иоанн Филопон (Александрийский, ок. 490-570), который ввел понятие «запечатленная сила». По вложенному в неё смыслу, она передает энергию внешнего толчка телу, и сохраняется в нём, расходуясь по мере движения. Он же впервые вводит понятия «динамика», как кинетическая (двигательная) способность, и «энергия», как кинетическая (двигательная) сила, тем самым разделяя способность к движению и собственно движение. Без всякого сомнения, это выдающаяся догадка, которая осталась без внимания плеяды последующих натурфилософов, прошедших мимо, не уделив ей должного внимания.

Своё дальнейшее развитие теория импетуса нашла в работах парижского номиналиста Жана Буридана (1300 – 1358) в «Вопросах к физике Аристотеля», написанной после 1328 г., и в «Вопросах к сочинению Аристотеля «О небе», написанной около 1340 г.

«Импетусом» Буридан называет некую силу, которая исходит от движущегося тела и запечатлевается в движимом теле (см. Иоанн Филопон). Величина импетуса определяется как скоростью, сообщенной движимому телу, так и его «количеством материи». «Количество материи» является «мерой импетуса» в теле. В этом состоит причина того, что «труднее остановить большое быстро движущееся колесо мастера, чем маленькое (вращающееся с той же скоростью)».

Буридан утверждал, что «импетус» продолжался бы до бесконечности, если бы не уменьшался и не разрушался от противоположности, оказывающей сопротивление, или еще от чего-либо, склоняющего к противоположному движению. «Движущее, приводя в движение движимое, запечатлевает некий импетус, т.е. некоторую силу, способную двигать это тело в ту сторону, в которую движущее его двигало: вверх, вниз в сторону или по кругу» [2, c. 131].

Таким образом, он говорит об «импетусе» и как о «движущей силе», и как о причине продолжения движения. Буридан считал «импетус» постоянным качеством движущегося тела. Он запечатлен в этом теле таким образом, как магнитные свойства запечатлены в железе. Как постоянное качество, «импетус» растрачивается не сам по себе, а только вследствие сопротивления среды, или «противоположного сопротивления» тела, что в последствии дало основание Ньютону сформулировать свой Первый закон механики.

Для нас важно, что Буридан увязывает «импетус» не только со скоростью, но и с «количеством материи», которое, вслед за Ньютоном, сегодня мы привыкли именовать как «масса». Но, кроме этого, особую важность приобретает его сравнение «импетуса» с магнитной силой, которая, по природе своего взаимодействия тождественна гравитационной силе. По Буридану «импетус» это не только первичный толчок к движению (приобретённый импульс), но и свойство продолжительного движения (инерция).

Серьезным недостатком воззрений Буридана, было использование термина «импетус» (импульс) в смысле силы, что и определило неверное направление формирующейся в то время классической механики.

В дальнейшем теорию импетуса развил ученик Жана Буридана Николай Орем (ок. 1325 – 1382), который укрепил ошибку Буридана: «я утверждаю, что это (импетус) в итоге является причиной ускорения тяжелого тела. Тот факт, что ускорение тяжелого тела происходит в начале, приводит к тому, что тело приобретает подобный импетус. Этот импетус и помогает телу осуществлять движение» [4].

В последующем именно это предположение, что импульс, является исключительной движущей силой в движении, и привело Ньютона к формулировке его Второго закона механики.

Но, до этого «запечатленная сила» Иоанна Филопона была заменена Рене Декартом на понятие «количество движения», без его математической формализации. Эту формализацию провёл уже Исаак Ньютон (1642 – 1727).

Ньютон впервые формализует понятие «количество движения»:

«Количество движения есть мера такового, устанавливаемая пропорционально скорости и массе» [5, c. 24].

И хотя Ньютон не прописал, что «количество движения» соответствует произведению массы тела на его скорость, из общих его рассуждений на эту тему этот факт становится очевидным, поэтому в ньютоновской формулировке «количество движения» формализуется в выражении:

p = m * u    (1)

Далее Ньютон пишет:

«Таким образом, ускорительная сила так относится к движущей, как скорость к количеству движения.

В самом деле, количество движения пропорционально скорости и массе, движущая же сила пропорциональна ускорительной и массе, ибо сумма действий ускорительной силы /2/ на отдельные частицы тела и составляет движущую силу его» [5, c. 29].

В этом пассаже Ньютон, производит неявную подмену «количества движения» (m*u) на движущую силу пропорциональную ускорительной силе и массе тела. Поскольку в этой формулировке вместо кинетического определения ускорения, он воспользовался динамическим определением силы, то она приобрела двусмысленность. В этом случае движущая сила соответствует произведению ускорительной силы на массу тела. Но поскольку сила сама по себе должна иметь в своем составе массу, то получается, что речь идёт о силе гравитационного взаимодействия, где мы видим произведение масс гравитационного центра и его стеллита.

Таким образом, под движущей силой Ньютон понимает силу гравитационного взаимодействия, а под ускоренной силой ускорение свободного падения, поэтому он и формализовал свой Второй закон в том виде, как он сегодня формулируется в классической физике. Но у него речь шла исключительно о гравитационном взаимодействии, а последующие толкователи перетолмачили его вывод в выражение, которое сам Ньютон не использовал:

F = m * a    (2)

Подмена силы импульсом, которую предложил Буридан, и которую принял Ньютон, говорит о том, что Ньютон был ещё только на пороге понимания сути классической физики, но не успел его перейти, и самое печальное то, что никто более не решись его переступить. Так ошибка в подмене силы на импульс и сохранилась до сего дня. Продолжать жить с этой ошибкой, или все же набраться духу провести необходимую реформу классической физики, это уже дело будущих поколений.

Я не буду приводить критику современного концепта основ классической физики, основываясь на том, что любой грамотный человек сам в состоянии сделать правильный для себя вывод о том, какою позицию занять в отношении проводимой реформы неоклассической физики открывающейся данной статьёй.

ОСНОВЫ НЕОКЛАССИЧЕСКОЙ ФИЗИКИ

Понятия «количество движения» и «сила» тождественны, и формализуются произведением количества материи (массы) m механической системы на её скорость u в пространстве, которое обозначается латинской буквой «F»:

F = m * u    (3)

В качестве единицы измерения силы предлагается Картез (кг*м/с), от латинского варианта фамилии Декарта, как дань уважения введению в научный оборот понятия «количество движения».

По своей физической сути, сила представляет собою динамическую характеристику движения механической системы обладающей определённой пространственной скоростью и массой. При этом скорость может быть постоянной, средней или мгновенной, в зависимости от решения конкретной задачи.

В случае постоянной скорости (u = const), сила является постоянной во всем интервале исследуемого интервала времени движения объекта;

В случае средней скорости (u_ср = ½(u_min + u_max)), сила определяет среднюю динамику объекта при его переменных скоростях во время исследуемого интервала времени;

В случае мгновенной скорости (u_t = u₀ + at.), сила характеризует динамику объекта в конкретный момент времени при du → 0, при линейно переменной скорости.

Отношение силы ко времени исследуемого интервала времени есть механический импульс, обозначаемый латинской буквой «Y»:

Y = F / Δt    (4)

Y = m * a    (5)

где, а = ∆u / Δt – ускорение (м/с²)

При Δt = 1 Y = |F|

В качестве единицы измерения механического импульса предлагается Ньютон (кг*м/с²), как единица, уже закреплённая в классической механике.

По своей физической сути механический импульс представляет собой динамику объекта, перемещающегося в пространстве с ускорением а, или мгновенную силу в единицу времени. При этом сила и ускорение движения могут быть постоянными на протяжения всего исследуемого интервала времени, или средними в интервалах (F₁,F₂), (a₁,a₂), либо мгновенными в любой момент времени исследуемого состояния механической системы из предположения их переменности в других точках пространства.

Произведение силы на пройденный механической системой путь есть работа, обозначаемая латино-кириллической буквой «А»:

А = F * L    (6)

A = m * u * L    (7)

A = Y * L * Δt    (8)

А = К * Δt    (9)

где, L – путь пройденный механической системой за интервал времени Δt (м);

К – кинергия (мгновенная кинетическая энергия) механической системы в единицу времени (Дж) во всём исследуемом интервале времени.

В случае, если механическая система в разные моменты времени пути обладает разным значением кинергии, то работа вычисляется, как среднее значение, из выражения:

А = ½(К₁ + К₂) * Δt    (10)

где, К_i – кинергии механической системы в крайних точках рассматриваемого интервала времени, при условии их линейного изменения внутри этого интервала.

В случае, если кинергия изменяется внутри исследуемого интервала времени нелинейно, то среднюю работу по интервалу вычисляют из выражения:

А = (1/n)(ΣК_n)Δt    (11)

где, ΣК_n – сумма кинергий в интервале времени Δt /3/.

В качестве единицы измерения работы предлагается Лейбниц (Дж*с), как дань уважении первой попытке научного описания понятия «энергия» в термине «живая сила».

По своей физической сути работа есть совокупная энергетическая динамика механической системы в интервале пройденного ею пути за время Δt, которая измеряется произведением кинергии на продолжительность процесса изменения энергетического состояния механической системы.

Кинергия, это всегда мгновенная кинетическая энергия механической системы, которая соответствует современному понятию мощности процесса изменения её энергетического состояния, вычисляемая из выражений:

К = A / Δt    (12)

К = m * u * L / Δt    (13)

К = m * a * L    (14)

К = m * u²    (15)

К = F * u    (16)

К = Y * L /4/    (17)

В случае линейно переменной скорости в исследуемом интервале времени, кинергия вычисляется как средняя величина этого интервала из выражения:

К = m * ½(u₁² + u₂²)    (18)

При u₁ = 0

К = ½mu_max² /5/    (19)

В наиболее общем виде, при всех исходных переменных, кинергия определяется из выражения:

К = ∫∫∫∫(muL/t)(dm,du,dL,dt)    (20)

ПРИЛОЖЕНИЯ НЕОКЛАССИЧЕСКОЙ ФИЗИКИ

1. Гравитационное взаимодействие.

Гравитационное взаимодействие в соответствии с известным законом Ньютона определяет гравитационный импульс:

Y_γ = γmM / R²    (21)

Y_γ = m * g    (22)

где, γ – гравитационная постоянная;

М – масса гравитационного центра системы;

m – масса гравитационного сателлита системы;

R – расстояние между центром сателлита и гравитационным центром системы;

g = γM/R² – ускорение свободного падения сателлита в направлении гравитационного центра.

Сила гравитационного взаимодействия определяется из выражения:

F_γ = Y_γ * Δt    (23)

F_γ = Y_γ *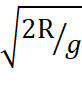  = Y_γ *  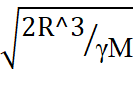   (24)

где, Δt – время радиального движения сателлита в направлении гравитационного центра системы /6/.

2. Вращательное движение.

Центробежный импульс определяется из выражения:

Y_цб = m * ω² * R    (25)

где, ω = u_цб/R – угловая скорость сателлита на орбите (1/с);

u_цб = u_τ√2 /7/;

u_τ – тангенциальная линейная скорость сателлита на орбите (м/с).

ω = u_τ√2/R

Тангенциальный импульс определяется из выражения:

Y_τ = ½Y_цб = ½(m*ω²*R)    (26)

Центробежная сила для точки выхода с орбиты вычисляется из выражения:

F_0цб = Y_цб * Δt = F_0τ√2   (27)

 Δt = 1 с

Равновесие сателлита на гравитационной орбите обеспечивается балансом Y_цб = Yγ.

При Y_цб > Yγ, сателлит удаляется от гравитационного центра, при Y_цб < Yγ, сателлит приближается к гравитационному центру.

Если тело покидает орбиту вращательного движения, в случае разрыва кинематической связи сателлита с центром его вращения, и находится при этом только под воздействием центробежного импульса, то угол его выхода с орбиты, за счет одновременного воздействия центробежного и тангенциального импульсов, составляет arctg√2  = 54,7356⁰ (54⁰ 44’ 8,2’’) относительно касательной к его орбите. При этом линейная скорость уходящего под этим углом с орбиты тела равна u_τ√3, а динамика его движения определяется равнодействующей двух сил: тангенциальной, направленной по касательной к орбите вращения, и центробежной, направленной по радиусу орбиты в противоположном от центра вращения направлении:

F_с = (F_цб² + F_τ²)^1/2 = F_τ√3  = F_цб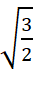    (28)

Сила вращательного движения «циркуцион» (circuitio) имеет максимальное значение во время схода сателлита с орбиты. В дальнейшем её значение уменьшается в соответствии с уменьшением скорости движения механической системы:

u_t = u₀ – ½at    (29)

где, u₀ – начальная скорость механической системы, в момент её выхода с орбиты;

а – результирующее ускорение торможения от сопротивления среды и гравитационного воздействия на механическую систему.

Подводя итог проведенному исследованию, необходимо отметить, что самая большая проблема неоклассической физики – это научиться отличать реальный факт от его виртуальной фантазии «аля факт».

Если мы говорим «импульс», то это кратковременное действие, которое описывается ускорением. Если мы говорим «сила», то это протяжённое во времени действие, и должно описываться понятием скорость.

Когда мы сегодня говорим «центробежная сила», на самом деле речь идет о «центробежном импульсе», так как собственно результирующая (центробежная+тангенциальная) сила появиться лишь после того, когда тело покинет свою орбиту.

То, что Ньютон понимал под «центростремительной силой» фактически является «гравитационным импульсом», который к вращательному движению не имеет никакого отношения, он всего лишь волею случая оказался вовлечённым в него. Центростремительной силы в природе не существует, также, как и центростремительного ускорения. Это серьёзная ошибка Ньютона, которую также необходимо удалять из неоклассической физики, заменив понятие «центростремительная сила» понятием «кинематическая связь».

И так далее и тому подобное.

Только, когда сознание сможет вырваться из этого королевства «кривых зеркал», оно сможет увидеть тот реальный мир, в котором обитает. К сожалению, пока, несмотря на все достижения научно-технического прогресса, наше сознание существует в ирреальном мире виртуальных иллюзий, и их научное объяснение мало чем отличается от хрустальных сфер Птолемея, на которых до Коперника все видели реальное движение звезд и планет на нашем небосводе.

Примечания

/1/ То, что изменение скорости было знакомо Аристотелю, следует из его высказывания: «Кроме того, движение не ускорялось бы под конец, если бы они двигались под действием силы и выдавливания, так как все [тела] по мере удаления от того, что сообщило [им] насильственный толчок, движутся медленнее и откуда движутся насильственно, туда – не насильственно» [1, т. 3, с. 289].

/2/ Используя термин «ускорительная сила» в отношении «ускорения», Ньютон, дает нам основание утверждать, что он еще не освоил границы между кинематикой и динамикой, что в последствии также стало основанием для подмены им силы импульсом.

/3/ В более сложных случаях, когда изменение кинергии в течение исследуемого интервала времени происходит хаотично, используют более сложный математический аппарат.

/4/ В этом выражении L соответствует пути, пройденному системой под воздействием импульса Y между энергетическим состояниями К = 0 и К = max, из предположения, что-либо импульс был приложен к системе в начале пути, либо она приобрела силу, по модулю равную импульсу, от его воздействия в конце этого пути.

/5/ Это выражение соответствует принятому сегодня значению кинетической энергии в классической физике, когда кинергия вычисляется как среднее значение, из предположения равенства нулю начальной скорости механической системы в исследуемом интервале времени [3].

/6/ В случае движения сателлита в противоположную сторону вычисляется сила, которую необходимо приложить к сателлиту, чтобы удалить его от гравитационного центра.

/7/ Это соотношение центробежной и тангенциальной скоростей можно наблюдать на соотношении первой и второй космических скоростей: 7,91*√2 = 11,19, а также при бросании «молота» на соревнованиях, когда «молот» уходит с орбиты под углом 54,736⁰ к касательной. При этом геометрический вывод этого соотношения убедительно доказывает, что при вращательном движении тангенциальная сила формирует исключительно силу центробежную, и не может сформировать центростремительную, поэтому её в природе и не существует. То, что Ньютон принимал за центростремительную силу, фактически является кинематической связью сателлита с центром его вращения. При разрушении этой связи сателлит всегда находится под воздействием только результирующей силы вращательного движения «циркуциона», и покидает траекторию вращательного движения.