Реализация алгоритмов построения вероятностных цепочек с использованием технологии .Net

1. Введение

В настоящей работе рассмотрен метод моделирования и прогнозирования динамики изменения социально-экономических данных, в частности в задачах распределения ресурсов, основанный на использовании одного класса дискретных динамических систем, а именно вероятностных цепочек. Вероятностные цепочки были впервые изучены в работах М. Сониса и Д. Хьюинса [1-4]. Логистические и логарифмически-линейные цепочки были успешно использованы в работах [5, 6, 7] для построения прогноза для данных различной природы.

В статье детально рассмотрены два вида вероятностных цепочек: с логистическим и с линейно-логарифмическим ростом. В целях реализации алгоритмов построения данного вида цепочек была разработана программа «PC predictor» на языке C# в среде Microsoft Visual Studio .NET. Кроме того, в работе рассмотрена сложность разработанных алгоритмов в программе «PC predictor».

Программный комплекс «PC predictor» применён для примера данных безработицы в процентах от общего числа населения по странам СНГ. Показано, что программа выполняет прогноз на заданный период времени, который может быть использован для исследования динамики изменения данных.

2. Основные определения

Вероятностный вектор – это совокупность величин p_i, таких, что
0≤p_i≤1, где i=1,..n, n – число групп или территорий, и .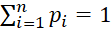

Дискретная вероятностная (1,n)-цепочка – это последовательность вероятностных векторов вида:

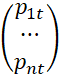, t=0,1,…; .

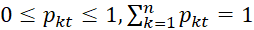Любую нелинейную вероятностную цепочку можно представить набором строго положительных порождающих функций – преобразований над вероятностными векторами. Так, k-й элемент вероятностного вектора в момент времени t будет иметь вид

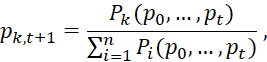
где P_k(p₀,…, p_t) – строго положительная порождающая функция, и k = 1,..., n, t = 0, 1, …

Вероятностные цепочки с логистическим ростом определяются набором порождающих функций

P_k(p)=γ_kp_k,

где γ_k>0, k=1,2,…, n – скорость прироста или снижения доли одного вида ресурса на территории k или k-ого вида одного ресурса на одной территории (который также является долей от совокупности всех рассматриваемых видов одного ресурса) и задаются формулой

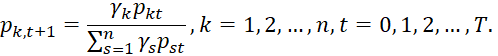
Линейно-логарифмические вероятностные цепочки задаются порождающими функциями Кобба-Дугласса:

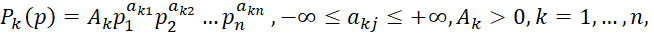
где A₁,..., A_n и элементы матрицы 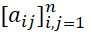параметры, определяемые в контексте задачи. Параметры вычисляются с помощью трехшагового метода наименьших квадратов.

Линейно-логарифмические вероятностные цепочки могут быть представлены в следующем виде:

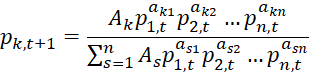
где k = 1,..., n,t = 0, 1, 2,..., T.

3. Построение цепочки с логистическим и линейно-логарифмическим ростом в программном комплексе «PC predictor»

В рамках работы была реализована программа, позволяющая для различных социально-экономических данных строить модели прогноза двух типов: основанных на вероятностных цепочках с логистическим ростом и на логарифмически-линейных цепочках. Программа написана на языке C# в среде Microsoft Visual Studio .NET [8].

Программа по исследуемым эмпирическим данным выполняет их интерполяцию, далее вычисляет экстраполяцию на заданный интервал времени, затем визуализирует полученные результаты с помощью графического представления. Пользователю предоставляется возможность с помощью панели управления загрузить массивы эмпирических данных, размещенных в файле в формате Excel. «PC predictor» составляет вывод о качестве анализируемых данных, используя для этого проверку статистическими критериями. Пользователь имеет возможность задать любой период времени для построения прогноза с помощью ввода целого числа в панели управления, а также выгрузить вычисленные значения и сохранить их в файле в формате Excel.

Приложение представляет собой MDI-форму, с помощью которой, можно импортировать таблицу из Excel-файла, содержащего эмпирические данные. MDI-форма состоит из окна, в котором отображается смоделированный график, соответствующий построенным моделям вероятностных цепочек. Также сверху MDI-формы имеется небольшая панель, содержащая кнопки управления, при нажатии на которые можно получить результаты вычисления статических критериев для исследуемых данных, выбрать группу из исследуемой совокупности, которая будет взята за стандарт, а также период, на который будет производиться экстраполяция. Также в родительской форме доступен экспорт вычисленной модели в Excel-файл.

При написании данной программы были использованы следующие библиотеки Microsoft.Office.Interop.Excel и MathNet.Numerics.LinearAlgebra [9]. Первая из них позволяет работать с Excel-файлом, производить обращение к элементам, получать данные и записывать их в файл. Вторая библиотека помогает производить простейшие математические операции линейной алгебры.

В программе реализовано несколько классов:

1. ProbabilisticChain.cs

В классе реализованы методы LogisticPorabalisticChain для вычисления цепочек с логистическим ростом и LinearLogarithmicPorabalisticChain для вычисления цепочек с линейно-логарифмическим ростом.

2. Statistics.cs

В классе реализовано вычисление статистических критериев: Стьюдента, Шапиро-Уилка, Фишера для исследуемых эмпирических данных, а также для результатов построенных вероятностных цепочек.

3. Program.cs

Класс, содержащий метод Main(), запускающий главную форму программы.

4. StatisticalTables.cs

Класс содержит в себе статистические таблицы, необходимые для получения вывода об удовлетворении нулевой либо альтернативной гипотезе вычисленных статистическими критериями результатов.

5. Form.cs

Класс-форма, который появляется при открытии приложения. Она содержит методы, обрабатывающие события главного меню и открывает дочерние окна. Здесь происходит непосредственно прогнозирование, построение моделей, а также импорт и экспорт файлов.

4. Сложность построения алгоритмов с логистическим и линейно-логарифмическим ростом

Рассмотрим сложность построения алгоритмов цепочек с логистическим и с линейно-логарифмическим ростом, реализованных с использованием технологии .Net.

Утверждение 1

Сложность алгоритма построения цепочек с логистическим ростом составляет O(n⋅(T+T_prog)), где T – количество лет, по которым имеются эмпирические данные, T_prog – количество лет, на которое строится прогноз, n – количество участников.

Доказательство

Сложность алгоритма определяется числом операций [10]. Рассмотрим операции, выполняемые программой PC Predictor при построении цепочек с логистическим ростом:

1) Смена местами двух столбцов имеет сложность O(T);

2) Вычисление z_kt имеет сложность O(n⋅T);

3) Вычисление 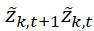,  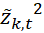и сумм полученных произведений и квадратов имеет сложность O(n*T);

4) Вычисление γ_k имеет сложность O(n);

5) Вычисление 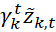 имеет сложность O(n*T);

6) Вычисление 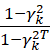, , 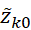,  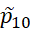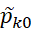имеет сложность O(n);

7) Вычисление 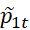 имеет сложность O(n*T);

8) Вычисление 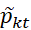 имеет сложность O(n⋅(T+T_prog)).

Общая сложность вычислений составляет: O(T)+O(n)+O(n⋅T)+O(n⋅(T+T_prog))

O(T)<O(n⋅T), O(n)<O(n⋅T), O(n⋅T)<O(n⋅(T+T_prog))

Общая вычислительная сложность O(n⋅(T+T_prog)), то есть линейна относительно размера матрицы данных n⋅(T+T_prog).

Что и требовалось доказать.

Утверждение 2

Cложность алгоритма построения цепочек с линейно-логарифмическим ростом составляет O(n²⋅(T+T_prog)), где T - количество лет, по которым имеются эмпирические данные, T_prog – количество лет, на которое строится прогноз.

Доказательство

Сложность алгоритма определяется числом операций [10]. Рассмотрим операции, выполняемые программой PC Predictor при построении цепочек с линейно-логарифмическим ростом:

1) Смена местами двух столбцов имеет сложность O(T);

2) Вычисление lnp_k,t+1-lnp_1,t+1 имеет сложность O(n⋅T);

3) Cмена порядка строк имеет сложность O(n⋅T);

4) Вычисление lnp_j,t  имеет сложность O(n⋅T);

5) Заполнение вычисленными данными матрицы X имеет сложность O(n⋅T);

6) Выполнение преобразований над матрицами с использованием библиотеки MathNet.Numerics.LinearAlgebra

Выполнение операции

Matrix<double>arry = Matrix<double>.Build.DenseOfArray(arrY) имеет сложность O(n⋅T).

Выполнение операции

Matrix<double> arrxtran = Matrix<double>.Build.DenseOfArray(arrX) имеет сложность O(n⋅T).

Выполнение операции

arrxtran = arrxtran.Transpose() имеет сложность O(n⋅T).

Выполнение операции

Matrix<double> arrx = Matrix<double>.Build.DenseOfArray(arrX) имеет сложность O(n⋅T).

Выполнение операции

Matrix<double> arrxMulti = arrxtran * arrx имеет сложность O(n²⋅T).

Выполнение операции

Matrix<double> arrResult = arrxMulti.Inverse() * arrxtran * arry имеет сложность O(n²⋅T);

7) Вычисление 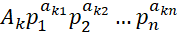 имеет сложность O(n⋅T);

8) Вычисление суммы 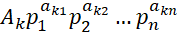 имеет сложность O(n);

9) Вычисление p_1,t+1 состоит из нескольких циклов, каждый из которых имеет следующие сложности:

O(n⋅(T+T_prog))

O(n²⋅(T+T_prog))

O(n⋅(T+T_prog))

Общая сложность вычислений составляет: несколько раз O(n*T) + несколько раз O(n²⋅T) + один раз O(n³) + несколько раз O(n⋅(T+T_prog)) + один цикл, где O(n²⋅(T+T_prog))

O(n⋅T)<O(n²⋅T)<O(n²⋅(T+T_prog))

O(n⋅(T+T_prog))<O(n²⋅(T+T_prog))

n<T+T_prog, n=O(T+T_prog)

Останется: O(n³)+O(n²⋅(T+T_prog))=O(n²⋅(T+T_prog)).

В итоге получаем, что общая вычислительная сложность составляет O(n²⋅(T+T_prog)).

Что и требовалось доказать.

5. Пример применения вероятностных цепочек к моделированию данных безработицы в процентах от общего числа населения по странам СНГ за 1996–2020 гг.

Рассмотрим данные о безработице в процентах от общего числа населения по странам СНГ за 1996–2010 гг., опубликованные Группой Всемирного банка [11]. Данные приведены в таблице.

Таблица

Безработица в процентах от общего числа населения по СНГ

Преобразуем эмпирические данные к последовательности значений p_kt, где каждое значение p_kt соответствует условиям 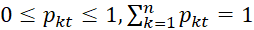. На рисунке 1 представлены графики изменения показателя безработицы эмпирических данных.

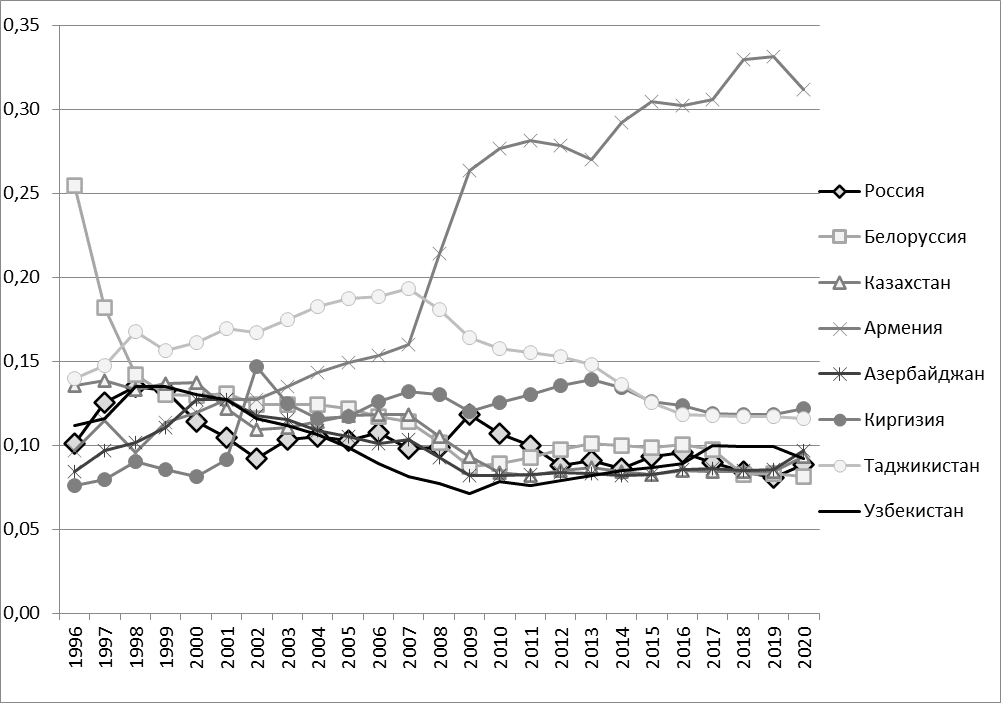
Рис. 1. Безработица в процентах от общего числа населения по странам СНГ. Эмпирические данные

Построим цепочки с логистическим ростом, за стандарт возьмём данные о безработице России. Интерполяцию выполним с 1996 по 2010 гг. Экстраполяцию с 2011 по 2020 гг. На основе полученных данных построим графики изменения показателя безработицы смоделированных данных за 1996–2020 гг. На рисунке 2 представлены графики изменения показателя безработицы смоделированных данных.

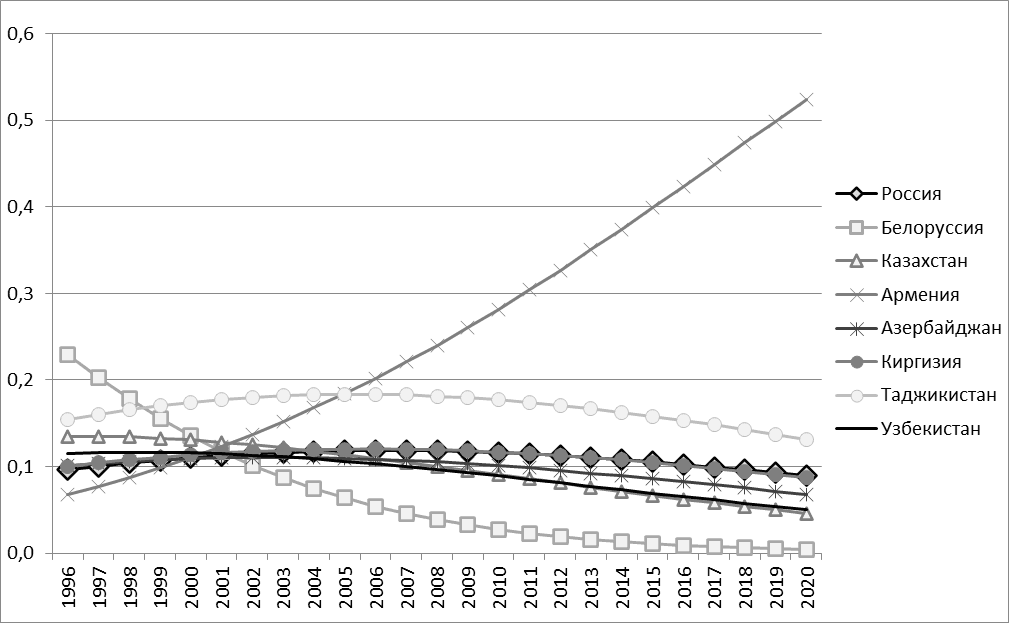
Рис. 2. Безработица в процентах от общего числа населения по странам СНГ. Вероятностные цепочки с логистическим ростом

Построим цепочки с линейно-логарифмическим ростом, за стандарт возьмём данные о безработице России. Интерполяцию выполним с 1996 по 2010 гг. Экстраполяцию с 2011 по 2020 гг. На основе полученных данных построим графики изменения показателя безработицы смоделированных данных за 1996–2020 гг. На рисунке 3 представлены графики изменения показателя безработицы смоделированных данных.

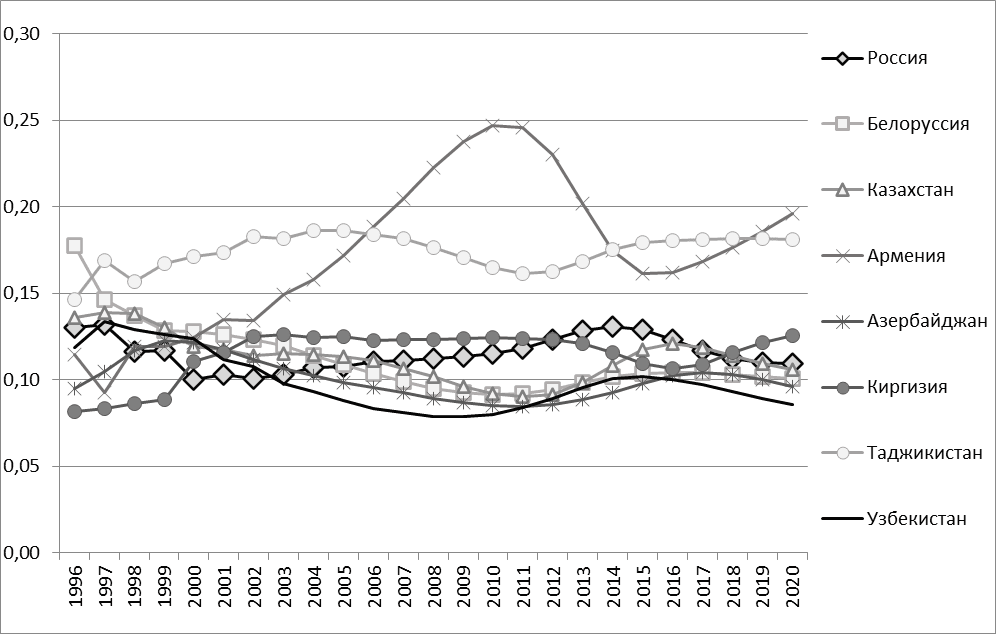
Рис. 3. Безработица в процентах от общего числа населения по странам СНГ. Вероятностные цепочки с линейно-логарифмическим ростом

6. Заключение

В представленной статье показаны алгоритмы построения вероятностных цепочек с логистическим и линейно-логарифмическим ростом. Приведены основные определения и представлены формулы для построения вероятностных цепочек. Кроме того, приведено подробное описание разработанных программ для построения вероятностных цепочек с использованием технологии .Net.

В статье проведен анализ сложности алгоритмов построения вероятностных цепочек с логистическим и линейно-логарифмическим ростом, реализованных автором в программе, написанной средствами технологии .Net.

В исследовании продемонстрировано применение вероятностных цепочек с логистическим и линейно-логарифмическим ростом на примере данных о безработице в процентах от общего числа населения по странам СНГ за 1996–2020 гг. Интерполяция данных проведена на период с 1996 по 2010 год, и экстраполяция на период с 2011 по 2020 год.