Распространение интеллектуальных средств автоматизации на объектах нефтегазовой отрасли трансформирует существующие системы управления на них. Данный процесс предполагает реализацию «цифровизации производства», которая обеспечивает повышение эффективности производственного процесса предприятия.
Процессы перекачки нефти характеризуются неопределенностями в исходных данных в условиях недостатка информации о протекающих процессах. Интеллектуальные средства автоматизации при интеграции с системой управления способны идентифицировать модель объекта, влияние состояния агрегатов, что позволяет учитывать особенности протекающих процессов управления. Большое количество технологических параметров, влияющих на процессы перекачки нефти, сказывается на точность определения технологических показателей объекта [1-4].
Для эффективного управления процессами перекачки необходимо своевременно производить оценку показателей качества нефти и осуществлять управление перекачкой исходя из требуемого качества. Интеллектуальные средства автоматизации способны решать данные задачи, что предполагает необходимость их применение на нефтеперекачивающей станции (НПС). Одни из наиболее известных подходов реализации программных продуктов интеллектуальных средств автоматизации выполнены на основе работы нейронной сети, предиктивной аналитики, а также виртуального анализатора.
Виртуальные анализаторы, работающие на основе применения линейной регрессии – это интеллектуальные средства автоматизации, реализующие математические функции для выполнения оценки состояния работы агрегатов, устройств, а также состояния сырья, продуктов, полупродуктов. Их применяют для оперативного ведения обработки данных, которых собирают на предприятии, и применения результатов работы анализатора для аргументации инициации изменений в ведении технологического или в целом производственного процесса.
Виртуальные анализаторы реализуются путем применения параметров, описанные в виде множеств:
M= f(X, Y, F, R), (1)
где X – множество входных воздействий;
Y – множество выходных воздействий;
F – множество внешних воздействий;
R – множество матриц отношений.
Выбор входных X, выходных Y и внешних F воздействий относится к сложным задачам, для выполнения необходимы эмпирические данные о параметрах функционирования отдельных технологических участков. Реализация же полученных законов управления всей технологической линией, основывается на выборе и изменении параметров отдельных технологических участков. В случае моделирования технологических процессов в нефтяной отрасли применимы передаточные функции, которые описывают апериодический процесс в условии нормального режима работы объектов. Матрицы отношений входных и выходных воздействий R на параметрическом уровне описываются комбинированным методом.
Динамика процессов описывается передаточными функциями вида апериодического звена первого порядка:
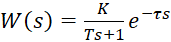, (2)
где s – оператор связи;
K – коэффициент усиления;
T – постоянная времени;
τ – время запаздывания.
Применение множества входных X и выходных Y воздействий требует выполнения следующих условий:
- необходимо исключение единичных величин, имеющих грубые погрешности;
- множества входных X и выходных Y воздействий должны иметь неслабую и несильную корреляцию;
- множества должны описывать работу объекта в нормальном режиме.
Условия корреляции множества входных X и выходных Y воздействий состоят в следующем:
- если коэффициент корреляции между i-ым входным и j-ым выходным параметрами равен или близок к нулю, то делается вывод, что данный входной параметр не влияет на выходной параметр и в моделировании не учитывается;
- если коэффициент корреляции между i-ым и j-ым входными параметрами равен или близок к единице, то делается вывод, что данные входные параметры сильно коррелируют между собой, значение одного можно вычислить через значение другого и в моделировании во избежание избыточности один из них не учитывается.
Параметры математических моделей виртуального анализатора описываются методом наименьших квадратов (матричный метод) при условии, что допускаются значений технологических параметров с приращением в 10 % от среднего.
Матричный метод наименьших квадратов реализуется следующим образом: матрица A определяет матрицу независимых факторов входных сигналов процесса, матрица B определяет матрицу результирующих значений процесса
Матрица А определяется по значениям входных переменных:
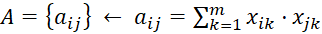. (3)
Вектор В – по значениям входных и выходных переменных:
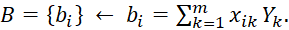(4)
Коэффициенты ki определятся как решение матричного уравнения:
A×K=B, (5)
где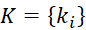 
– вектор коэффициентов полинома.
Коэффициенты полинома определяются по формуле
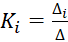, (6)
где ∆i – промежуточный определитель;
∆ – главный определитель.
Промежуточный определитель формируется на основе матрицы A, в которой в i-ым столбце заменяется на матрицу B.
Модель динамики процессов на объекте описывается следующей функцией:
- плотность нефти:
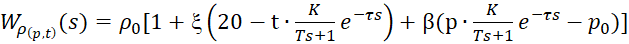, (7)
- содержание воды:
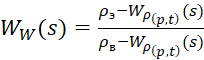. (8)
Нейронная сеть (НС) представляет собой совокупность нейронов, связанных между собой соответствующим образом. В основе нейросетевых методов лежит попытка компьютерного моделирования процессов обучения, используемых в живых организмах. Когнитивные способности живых существ связаны с функционированием сетей связанных между собой биологических нейронов – клеток нервной системы.
Рассмотрена возможность реализации НС модели многослойного персептрона (МСП).
Основной состав НС модели МСП состоит из трех основных слоев вычислительных элементов:
- входной слой, на который поступают сигналы из внешней среды;
- скрытый слой, используемый для увеличения вычислительной мощности сети;
- выходной слой, на котором формируется искомое решение.
Скрытый слой может состоять из нескольких слоев вычислительных элементов.
На рисунке представлена структура МСП вида (3-3-3-1 + 3-3-1), позволяющая реализовать задачи системы прогнозирования показателей качества. Данная структура представляет собой расчёт двух показателей качества, где расчёт второго показателя качества выполняет за счёт результата расчёта первого показателя качества.
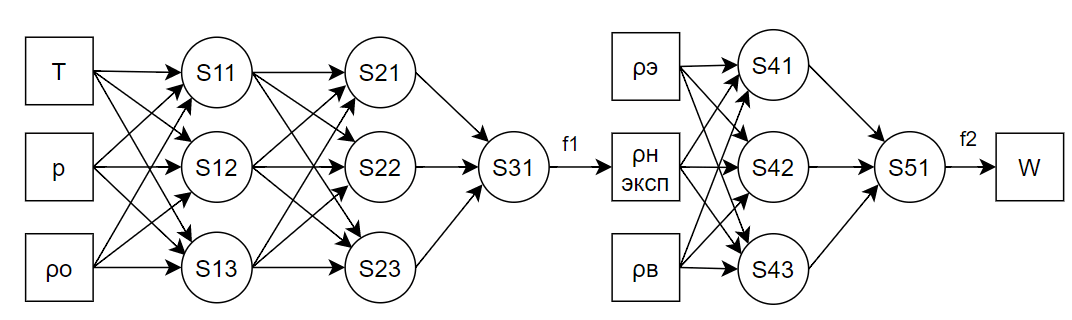
Рис. Структура МСП
Реализация НС требует устранения различий между множествами воздействий выполняется. Это возможно путем применения подхода минимаксной нормализации по формуле:
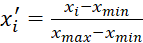, (9)
где xmin – минимальное значение множества x;
xmax – максимальное значение множества x.
Подразумевается, что каждое входное воздействие xi преобразуется в величину '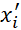
, что позволит выполнить сглаживание множества X.
Вид функции активации во многом определяет функциональные возможности НС и метод её обучения. В данной работе применима экспоненциальная функция активации, имеющая вид:
y=e-CS, (10)
где C – коэффициент ширины сигмоиды по оси абсцисс;
S – взвешенная сумма входных сигналов.
Данный вид функции активации позволит выводить область значений моделируемого выходного воздействия в диапазоне (0, ∞).
Взвешенная сумма входных сигналов (без учета порога нейрона) вычисляется по формуле:
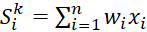, (11)
где wi – вес сигнала;
xi – значение сигнала, поступающий на вход нейрона.
Верхний индекс k взвешенной суммы входных сигналов означает номер слоя.
Функция активации НС выглядит следующим образом
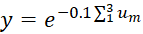, (12)
где 
– взвешенная сумма входных сигналов конечного скрытого слоя.
Обычно НС состоит из множества входных узлов, которые образуют входной слой; одного или нескольких скрытых слоев вычислительных нейронов и одного выходного слоя. Входной сигнал распространяется по НС в прямом направлении от слоя к слою. Многослойные персептроны успешно применяются для решения разнообразных сложных задач. При этом обучение с учителем выполняется с помощью такого популярного алгоритма, как алгоритм обратного распространения ошибки.
Особенностью обучения НС алгоритмом обратного распространения является его послойная реализация, начиная с последнего слоя к первому. Имеется следующий порядок его реализации:
- определение суммы ошибок:
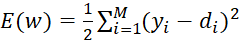, (13)
где di – ожидаемое (тестовое, эталонное) значение;
- определение производной ошибки:
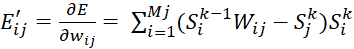, (14)
- проведение корректировки весов примем α=1:
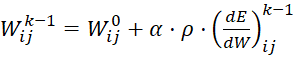. (15)
- определение значения концепта до тех пор, пока значение суммы ошибок не будет стремиться к нулю.
Если значение суммы ошибок стремиться к нулю E→0, НС считается обученной.
Преимущества применения модели нейронной сети MLP состоят в следующем:
- есть возможность изучать нелинейные модели;
- есть возможность изучения моделей в режиме реального времени.
К недостаткам модели нейронной сети MLP относятся следующие факторы:
- MLP со скрытыми слоями имеют невыпуклую функцию потерь, когда существует более одного локального минимума. Поэтому разные инициализации случайных весов могут привести к разной точности проверки;
- MLP требует настройки ряда гиперпараметров, таких как количество скрытых нейронов, слоев и итераций;
- MLP чувствителен к масштабированию функций.
Исходя из недостатков применение НС в системе управления технологическим процессом влечет за собой множество факторов, которые не позволят выполнить корректно интерпретацию результатов прогнозируемых параметров, поскольку их поведение не всегда возможно описать нормальным распределением. Исходя от этого, решено пренебречь применением данным методом для синтеза системы прогнозирования [5-9].
Одним из методов кластеризации данных, актуальных для обработки данных в режиме реального времени, является наивный байесовский классификатор. Данный тип метода обработки данных применяет теорему Байеса. Эта теорема предлагает метод оценки потенциала события процесса на объекте на основе заранее известных (на основе эмпирических данных) параметров, имеющие отношение к данному событию. Т.е. за счет теоремы Байеса возможно спрогнозировать совершение события Y по входным условиям X и их вероятности наличия в момент совершения события Y.
При реализации теоремы Байеса вычисляют условную вероятность, которая рассчитывается по формуле:
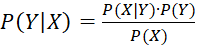, (16)
где PYX – условная вероятность события Y при реализации события X;
P(X|Y)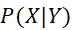
– вероятность события X при фиксированном событии Y;
P(Y) – вероятность события Y;
P(X) – вероятность события X.
При применении метода наивного байесовского классификатора для его реализации в системе прогнозирования необходимо учитывать условие, что применяющиеся в расчетах события X независимы друг от друга и не оказывают влияние на значения.
В силу поставленных требований установлено, что для реализации расчетов по методу наивного байесовского классификатора, необходимо в совокупности выполнить следующие условия:
- из модели (16) исключить из расчетов значение вероятности событий X P(X);
- иметь независимые ряды значений параметров (событий) X.
Вид математической модели наивного байесовского классификатора для системы прогнозирования технологических параметров НПС, описывающие выходные сигналы процесса Y, имеет вид:
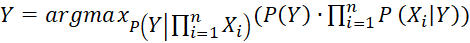. (17)
Одним из недостатков наивного байесовского алгоритма является то, что если класс и значение параметра не встречаются вместе, то оценка вероятности, высчитываемой с использованием частот, будет равна нулю. В итоге после перемножения всех вероятностей мы получим ноль. Чтобы исключить данный недостаток, требуется к каждой комбинации класса и значения параметра добавлять единицу, когда значение параметра нулевое.
Выполнен анализ интеллектуальных моделей системы прогнозирования отдельных технологических параметров при различных технологических режимах. Установлено, что не все методы, которые по характеристике применимы для реализации системы прогнозирования состояния технологического процесса, подходят для работы на НПС.
Независимо от точности выполнения вычислительных операций важным аспектом работы системы прогнозирования является его интерпретируемость, что позволяет выполнить проверку на полезность прогнозов модели. Линейная регрессия легко интерпретируется, однако она имеет значительную зависимость от того, каким образом сформированы множества воздействий и каким образом описана динамика процесса в определенный момент. НС имеют высокую точность вычислительных операций, однако имеются проблемы её интерпретации.
Наивный байесовский классификатор способен выполнять прогнозирование состояния показателей качества, однако для этого требуются наиболее точные эмпирические данные с большим количеством технологических параметров, способные выполнять прогнозирование состояния продукта. Это влечет за собой возможность реализации моделей на основе наивного байесовского классификатора в системе прогнозирования в качестве ИСА, способного определить состояния оборудования.
Таким образом, установлено, что:
- модели, построенные на основе линейной регрессии, имеют меньшую точность в сравнении с моделями, построенные на основе НС модели МСП, однако обладает наиболее ясной интерпретацией;
- модели, построенные на основе наивного байесовского классификатора, более пригодны для реализации прогнозирования состояния оборудования объекта, поскольку не способен наиболее точно определить значения показателей качества, а лишь предположить производственную ситуацию.
