Практически во всех отраслях научных знаний: физике, биологии, химии, математике, истории, лингвистике, социальных науках, технике и т.п. применяются графы. Наибольшей популярностью графы пользуются при исследовании коммуникационных сетей, систем информатики, химических и генетических структур, электрических цепей и других систем сетевой структуры. Не удивительно, что граф нашёл применения в алгоритмах сортировки, которые используются во всех языках программирования. Частным случаем графа является двоичное дерево поиска, которое применяется в алгоритме сортировки.
Для создания алгоритма древесной сортировки используют иерархическую рекурсивную структуру данных, которая называется двоичным деревом поиска. Оно имеет свойства связности и ацикличности. Связность – это свойство графа, которое обеспечивает маршрут между двумя различными вершинами. Ацикличность – это свойство графа, которое говорит об отсутствии замкнутых последовательностей соседних вершин и рёбер [2]. Небольшое двоичное дерево поиска проиллюстрировано на рисунке 1.
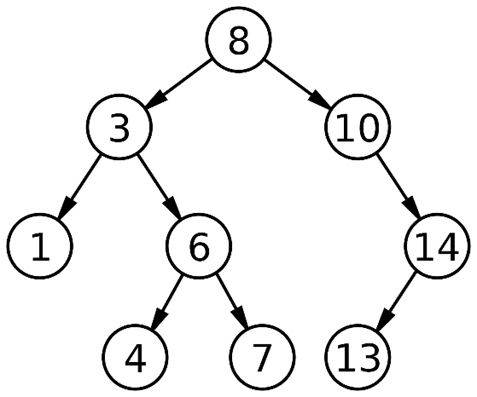
Рис. 1. Пример двоичного дерева поиска
Двоичное дерево можно разбить на составные части, которые называются узлами. Узел – это часть двоичного дерева, которая состоит из какого-нибудь значения и не более двух дочерних деревьев. Дочерними узлами (или поддеревьями) называют узлы (деревья), на которые ссылается родительский узел. Узел, который находится в самой вершине дерева называется корнем. Узлы, которые находятся в самом низу дерева и не имеют поддеревьев, называют листьями [1]. Так, например, для двоичного дерева на рисунке 1 определим корень, вершину, количество узлов и отношение между узлами со значениями 3, 1 и 6. Корнем является узел с числовым значением 8. Узлы со значениями 1, 4, 7, 13 – листья. Количество узлов – это количество вершин в графе, то есть 9. Узел со значением 3 является родительским для узлов со значениями 1 и 6. В свою очередь узел 1 и 6 являются дочерними для узла со значением 3.
Самое главное в этой структуре данных – это свойство, которое формулируется следующим образом: левый потомок имеет значение меньшее, чем родитель, а правый потомок имеет значение, которое больше или равно родителю [10]. То есть значения хранятся уже в отсортированном виде и их удобно использовать для решения определённых задач.
Построение таких деревьев происходит с помощью выполнения простой последовательности некоторых действий. Например, у нас есть массив данных. Пусть эти данные будут числовыми, а количество элементов будет равно 5-и. На рисунке 2 изображён набор из 5-и случайных числовых элементов.
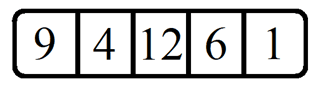
Рис. 2. Случайный числовой набор
Добавление реализуется по следующей схеме: сначала осуществляем поиск добавляемого элемента в дереве, затем, если его не находим, то выбираем подходящее место для нового узла. Если добавляемое значение меньше корня, то оно записывается в левое поддерево, в противном случае – в правое. Получим дерево, изображённое на рисунке 3.
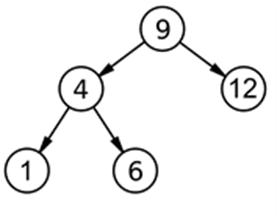
Рис. 3. Построенное дерево
Двоичное дерево может быть логически разбито на уровни. Корень дерева является нулевым уровнем, потомки корня – первым уровнем, их потомки – вторым, и т.д. Глубина дерева – это его максимальный уровень. Понятие глубины также можно сравнить с понятием пути, то есть глубина дерева есть длина самого длинного пути от корня до листа, если следовать от корня до потомка. Эффективность поиска по дереву напрямую связана с его сбалансированностью, то есть с максимальной разницей между глубиной левого и правого поддерева среди всех вершин [1]. Имеется два крайних случая – сбалансированное (рисунок 4) и вырожденное (рисунок 5) бинарное дерево.
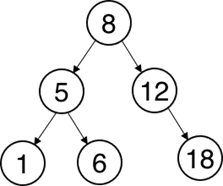
Рис. 4. Сбалансированное бинарное дерево
Каждый уровень сбалансированного дерева имеет полный набор вершин.
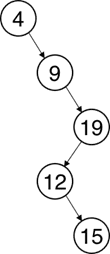
Рис. 5. Вырожденное двоичное дерево
На каждый уровень вырожденного дерева приходится по одной вершине. Время выполнения всех основных операций пропорционально глубине дерева. Таким образом, скоростные характеристики поиска в двоичном дереве поиска могут варьироваться от O(log2N) в случае сбалансированного дерева до O(N) – в случае вырожденного [3].
Приведение уже существующего дерева к идеально сбалансированному – процесс сложный. Проще балансировать дерево в процессе его роста (после включения каждого узла). Однако требование идеальной сбалансированности делает и этот процесс достаточно сложным, способным затрагивать все узлы дерева [2]. Зачастую данные, которые поступают для хранения в виде дерева, неотсортированные. Поэтому результирующее дерево будет достаточно сбалансированным.
Любой алгоритм имеет преимущества и недостатки. Для того чтобы сравнивать различные алгоритмы, нужно выбрать некие критерии, которые будут универсальны и смогут показать, насколько подходит алгоритм для выполнения поставленной цели. Такой критерий называется сложностью алгоритма. Она обычно измеряется двумя параметрами – временем и памятью. При оценке важна лишь асимптотическая сложность, т. е. сложность при стремлении размера входных данных к бесконечности. Допустим, некоторому алгоритму нужно выполнить 3n2 + 2n условных операций, чтобы обработать n элементов входных данных. При увеличении n на итоговое время работы будет значительно больше влиять возведение n в квадрат, чем умножение его на 3 или же прибавление 2n. Тогда говорят, что временная сложность этого алгоритма равна О(n2), т. е. зависит от размера входных данных квадратично. Также бывает линейная, константная, логарифмическая зависимости [3]. Рисунок 6 отображает динамику роста количества операций в зависимости от n.
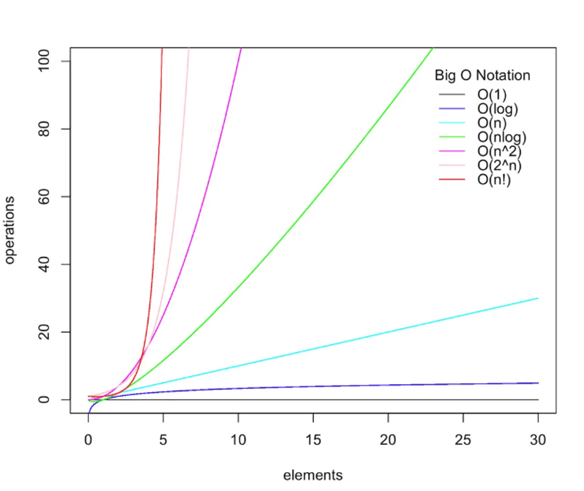
Рис. 6. График зависимости числа элементов от числа операций
В некоторых случаях более значимым является вопрос используемой алгоритмом памяти. Этот вопрос был особенно актуальным на ранних этапах развития компьютеров при ограниченных объемах компьютерной памяти, однако не потерял своей актуальности и на сегодняшний день. Алгоритмы могут использовать значительно больше памяти при увеличении размера входных данных, чем другие, но зато работать быстрее. И наоборот. Оценка сложности алгоритма по памяти (ёмкостная оценка) – это определение количество дополнительной памяти, используемой в процессе его выполнения. Как и при оценке временной сложности, так и при ёмкостной важна лишь асимптотическая сложность.
Оценим сложность алгоритма сортировки деревом. Процедура добавления объекта в бинарное дерево имеет среднюю алгоритмическую сложность порядка O(log2n). Соответственно, для n объектов сложность будет составлять O(nlog2n), что относит сортировку с помощью двоичного дерева к группе «быстрых сортировок» [9]. Однако сложность добавления объекта в разбалансированное дерево может достигать O(n), что может привести к общей сложности порядка O(n2). При физическом развёртывании древовидной структуры в памяти требуется не менее чем 4n ячеек дополнительной памяти (каждый узел должен содержать ссылки на элемент исходного массива, на родительский элемент, на левый и правый лист).
Первым этапом в работе алгоритма сортировки является получения данных, которые нужно отсортировать. Попросим ввести количество элементов для сортировки и запишем его в переменную size. После этого создадим массив с именем arr и размером size. Затем, с помощью цикла запишем в массив элементы, которые введёт пользователь. Теперь нам нужно определить тип сортировки – по убыванию, или по возрастанию. Введённое с консоли значение запишем в переменную sort_type. На рисунке 7 изображена блок-схема этих действий.
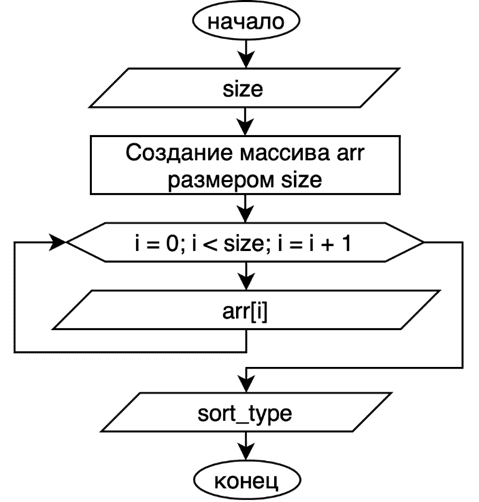
Рис. 7. Блок-схема создания и инициализации массива
Все необходимые сведения получены. Этап введения пользователем данных для сортировки завершён.
Построение двоичного дерева поиска
Для начала определим структуру узла дерева с именем Node. Она будет содержать 3 поля – указатель left на левый узел, указатель right на правый узел и само значение узла value. При построении двоичного дерева поиска нужно придерживаться правила: левое поддерево имеет значение меньшее, чем родитель, а правое поддерево имеет значение, которое больше или равно родителю [8]. При добавлении очередного элемента массива дерева будем сравнивать его со значением текущего узла. Чтобы перебрать все элементы массива, используем цикл for. Перед циклом создадим узел Node и указатель root на него. Затем зададим значение созданному узлу, равное начальному элементу массива. Этот узел будет корнем создаваемого дерева. В цикле создадим две переменные. Первая переменная p_current_node – указатель на текущий узел. Вторая переменная с именем inserted – булева. Она будет показывать, добавлен ли текущий элемент массива в дерево. Инициализируем переменной inserted значение false. Полученная блок-схема на рисунке 8.

Рис. 8. Блок-схема построения двоичного дерева поиска
Так как указатели на дочерние узлы будут заполняться по мере прохождения массива, то нам нужно «дойти» до узла, который подходит по значению, и у которого указатель на дочерний узел свободен. Этот алгоритм реализуем внутри цикла while. Условием выполнения цикла будет значение false у переменной inserted. Выход из цикла произойдёт, когда переменная inserted станет равна true. Будем присваивать true переменной inserted, при добавлении нового узла в дерево.
В теле цикла сравним добавляемый элемент массива с текущим узлом. Если элемент будет меньше, то проверим – есть ли в левом указателе текущего узла значение? Другими словами – имеет ли узел поддерево? Если не имеет, то создадим новый узел Node, присвоим указателю left текущего узла только что созданный узел и инициализируем полю value нового узла добавляемый элемент массива. Произошло добавление нового узла, что означает, что мы должны изменить переменную inserted на true. Если же в левом указателе текущего узла есть значение, то «перейдём в левое поддерево». То есть присвоим указателю p_current_node его поле left.
Так как значение добавляемого элемента массива может быть больше или равно текущему узлу, то нужно создать блок с условием, где будет осуществляться проверка этого. Внутри этого блока реализуем такое же «добавление поддерева», только указатели left заменим на right. То есть добавим или перейдём не в левое, а в правое поддерево. Полученный цикл while вставим на место блока «1», который находится в теле цикла for. Почему мы не будем балансировать полученное дерево? Во-первых, этот процесс является достаточно сложным. Во-вторых, данные, которые мы получили из массива, находились в неотсортированном виде. Поэтому с большой вероятностью дерево, будет достаточно сбалансированное и различные действия с элементами, будут происходить примерно за log2n операций.
Этап построения двоичного дерева поиска завершён.
Построение отсортированного массива
Сборка результирующего массива будет осуществляться путём центрированного обхода узлов уже построенного бинарного дерева поиска. Обход реализуем с помощью рекурсивной функции left_traversal, которая будет описана в структуре Node. Эту функцию мы сможем использовать для любого узла ранее построенного дерева. Эта функция будет принимать на вход указатель на массив, который ещё не отсортирован. Возвращаемое значение функции – это также указатель на массив. Вызов функции для определённого узла будет означать обход этого узла и запись всех значений, которые мы обошли в отсортированном порядке в массив, указатель на который мы передали в функцию. Алгоритм центрированного обхода: обходим левое поддерево, посещаем узел, после обходим правое поддерево. Посещение узла – это добавление значение текущего узла в массив на место указателя. То есть функция будет состоять из вызова этой же функции для левого поддерева, добавления в массив нового элемента на место указателя, переноса указателя на следующий элемент и вызова функции для правого поддерева. На рисунке 9 изображена блок-схема этого алгоритма.
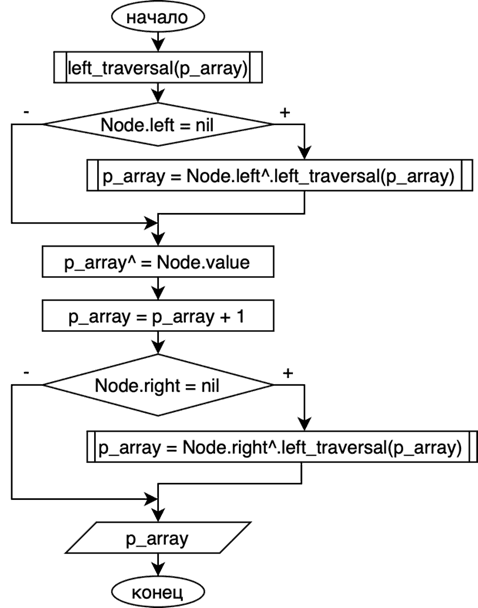
Рис. 9. Блок-схема алгоритма центрированного обхода дерева слева
Слово Node в этой блок-схеме означает текущий узел, nil – пустой указатель, а символ ^ означает переход по указателю. Вышеописанный алгоритм сначала обходит левое поддерево, посещает узел, а затем обходит правое поддерево. Если мы вызовем эту функцию у корневого узла ранее построенного дерева и передадим в неё указатель на неотсортированный массив, то алгоритм запишет в этот массив элементы, отсортированные по возрастанию. Чтобы отсортировать массив по убыванию, нам нужно будет описать функцию right_traversal в структуре Node, которая будет обходить сначала правое поддерево, посещать узел, а потом обходить правое поддерево. Блок-схема на рисунке 10.
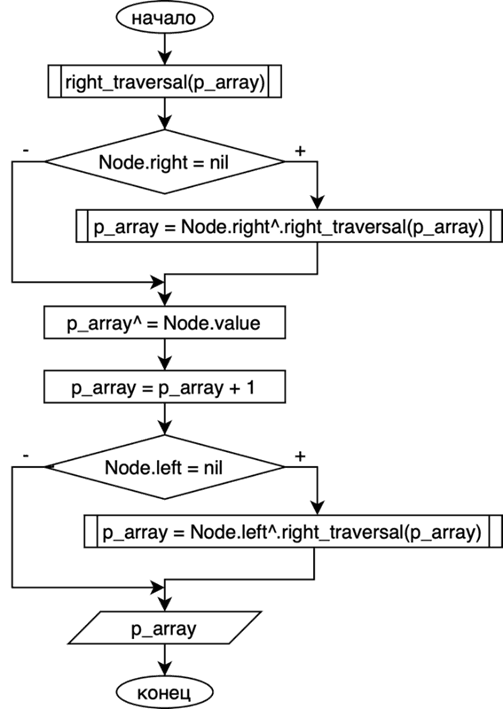
Рис. 10. Блок-схема алгоритма центрированного обхода дерева справа
В зависимости от того, какой тип сортировки указал пользователь, мы и будем вызывать определённые функции. Тип сортировки определяет переменная sort_type. Так, если sort_type равна 1, то мы вызовем для корня дерева функцию left_traversal, если же sort_type равно 2, то вызовем right_traversal. Во всех случаях будем передавать введённый вначале пользователем массив arr. Блок-схема на рисунке 11.
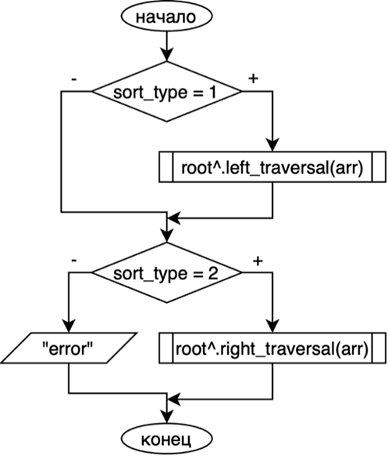
Рис. 11. Блок-схема выбора алгоритма обхода
Теперь наш массив отсортирован, и мы можем отобразить его элементы на экране.
Вывод отсортированных данных
Чтобы вывести элементы отсортированного массива, воспользуемся циклом. Переменная цикла i будет изменятся от 0 до size-1 с шагом 1. В теле цикла будем выводить i-ый элемент массива arr. Блок-схема на рисунке 12.
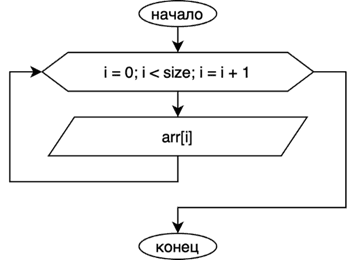
Рис. 12. Блок-схема вывода отсортированных данных
На экране пользователь увидит отсортированный в нужном порядке список элементов. На этом разработка алгоритма окончена.

.png&w=640&q=75)