Снижение уровня напряжений в слое адгезива при действии механических нагрузок за счет топологической оптимизации его микроструктуры и градиентных свойств

Постановка задачи: Изучить задачу топологической оптимизации слоя адгезива в трехслойном пакете при действии механической нагрузки и реализовать алгоритм получения оптимальной топологии конструкции и слоя припоя с целью снижения пиковых значений напряжений сдвига в них.

Рассмотрим термоупругий трехслойный пакет, конструкция которого приведена на рисунке 1. Пакет закреплен на одной балке, ко второй приложена сила F.

Область  заполнена дюралюминием с модулем Юнга и КЛТР равными Па и К^-1, соответственно. Материал области  – бронза с Па и  К^-1. Область  – область припоя, в которой необходимо найти оптимальную микроструктуру распределения заданного количества серебряного припоя с  Па и  К^-1. Размеры пакета в миллиметрах показаны на рисунке 1.

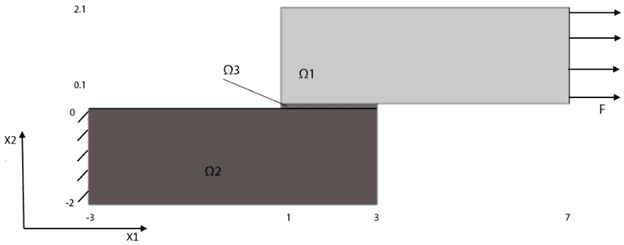
Рис. 1. Конструкция термоупругого трехслойного пакета

Для расчетов был использован МКЭ с линейными треугольными конечными элементами и неравномерной сеткой со сгущением в окрестности слоя адгезива. Разбиение приведено на рисунке 2.

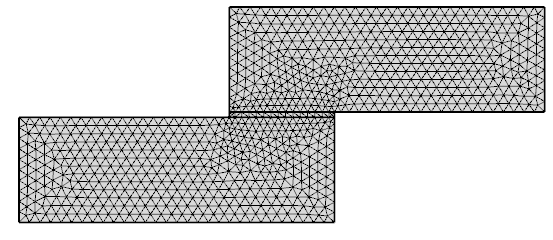
Рис. 2. Разбиение методом конечных элементов

С помощью метода SIMP была проведена топологическая оптимизация для решения задачи топологической оптимизации в трехслойном пакете при действии механической нагрузки.

Проблема топологической оптимизации для задачи снижения пиковых значений напряжений σ₁₂ в слое припоя может теперь быть сформулирована в виде

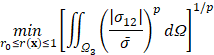 (1)

при ограничении

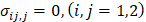в Ω, (2)

и изопараметрическом ограничении на физическую плотность  

 (3)

где γ обозначает долю материала припоя и 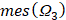 - площадь области припоя.

Для исключения эффекта «шахматной доски» в процессе оптимизации целевую функцию определим в виде линейной комбинации функции (1) и дополнительно введенной функции штрафа

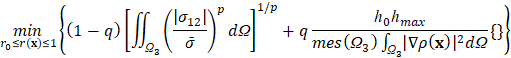 (4)

Второе слагаемое является функцией штрафа,  – первоначальный размер сетки конечных элементов и  – текущий размер сетки. Величина  – заданный коэффициент, позволяющий сбалансировать функцию цели и функцию штрафа друг с другом.

Решение задачи оптимизации производилось методом подвижных асимптот [1, с 360]. На рисунке 3 показана топология оптимальной микроструктуры слоя припоя.

Рис. 3. Топология оптимальной микроструктуры конструкции

Рис. 4. Топология оптимальной микроструктуры слоя припоя

На рисунке 3 показана топология оптимальной микроструктуры конструкции. На рисунке 4 показана топология оптимальной микроструктуры слоя припоя. Здесь красным цветом обозначены области, заполненные припоем, а белым цветом – пустоты.

На рисунке 5 представлены графики распределения напряжения сдвига по границам области припоя.

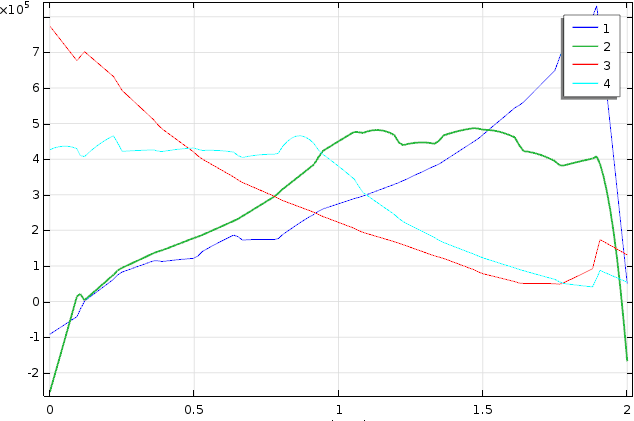
Рис. 5. Графики распределения напряжений сдвига по верхней (1,2) и нижней (3,4) границе области припоя

Заключение. Алгоритм топологической оптимизации использовался для оптимизации микроструктуры соединения с целью уменьшения пиковых напряжений в слое припоя. Результаты показывают, что полученная оптимизированная микроструктура значительно снижает пиковые напряжения в слое припоя. Это было достигнуто за счет более жесткой структуры на краю пакета, которая приводила к более низким пиковым напряжениям отслаивания наряду с плавным распределением напряжений вдоль слоя припоя.

This work was supported by the Russian Science Foundation RSF 16-11-10138-П.