Фазовый портрет является графическим изображением системы в многомерном пространстве (фазовой траектории), по координатным осям которого отложены значения величин переменных системы [1]. При использовании данного метода представления поведение переменных, зависимых от времени, для каждой начальной точки описывается фазовой траекторией. Совокупность таких фазовых траекторий для различных начальных условий и представляет собой фазовый портрет [2].
Благодаря построению фазового пространства становится возможно наглядно проследить за поведением системы в окрестности особой точки, а также удалении от нее.
Чтобы построить фазовый портрет необходимо провести вычислительный эксперимент. Работа ведется с математической моделью деформационного и термического упрочнения сплавов со сверхструктурой L12 с учетом разрушения дальнего атомного порядка в случае работы сверхдислокационных источников [3], которая представляет собой систему обыкновенных дифференциальных уравнений [4]:
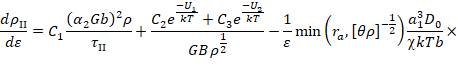
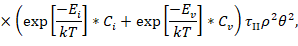
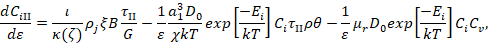
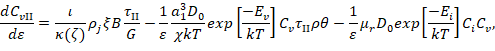
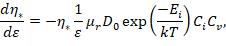
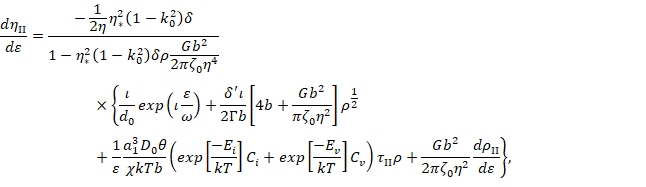
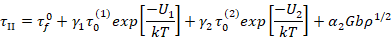
Вычислительный эксперимент заключается в вычислении системы при заданных параметрах и начальных значениях.
Для проведения данного эксперимента выбран набор параметров, соответствующий деформационному сплаву Ni3Ge при комнатной температуре и задан в системе Mathcad [5]:
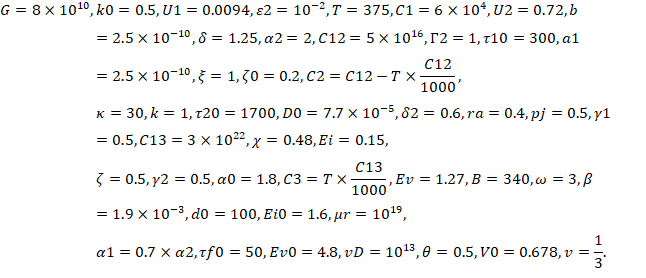
Данная модель в качестве независимой переменной использует деформацию e. Зависимыми переменными являются r (плотность дислокации), Cv (количество вакансий), h* (параметр дальнего порядка внутри антифазного домена), h (параметр дальнего порядка – упорядоченность во взаимном расположении атомов или молекул в веществе), ho (сумма h* и h). Переменные модели были переобозначены следующим образом: ρ → x0, Cv → x1, η* → x2, η → x3 и заданы в виде начальных значений, т.к. задача Коши считается поставленной, когда имеется система и начальные значения, кроме того, для построения фазового портрета необходимо построить набор кривых, поэтому были проварьированы значения r.
По результатам данного эксперимента построены зависимости параметров (рисунок 1) математической модели.
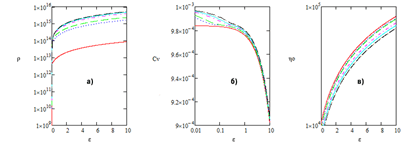
Рис. 1. Зависимости: плотность дислокации от деформации (а), количество вакансий от деформации (б), сумма параметров дальнего порядка от деформации (в)
На рисунке 1 (а) видно, что увеличивается плотность дислокации, а на рисунке 1 (в) сумма параметра дальнего порядка. Рисунок 1 (б) показывает, что количество вакансий уменьшается.
В работе построены двухмерные фазовые портреты (рисунок 2).
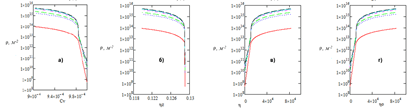
Рис. 2. Двухмерные фазовые портреты
Графики имеют следующие зависимости: плотность дислокации от количества вакансий (рисунок 2 (а)), плотность дислокации от параметра дальнего порядка внутри антифазного домена (рисунок 2 (б)), плотность дислокации от параметра дальнего порядка (рисунок 2 (в)), плотность дислокации от суммы параметров дальнего порядка (рисунок 2 (г)).
Можно заметить, что особая точка неустойчивая, потому что прямые не стремятся друг к другу, а наоборот отдаляются от точки.
Помимо двухмерных графиков представления фазового портрета был построен трехмерный график с помощью инженерно-математического программного обеспечения OriginPro [6] на основании переменных математической модели: r (плотность дислокации), Cv (количество вакансий), ho (сумма параметров дальнего порядка) (рисунок 3).
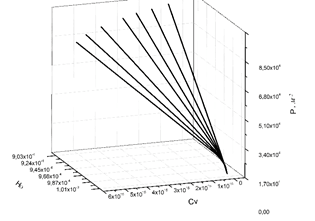
Рис. 3. Трехмерный фазовый портрет
На рисунке 3 приведен трехмерный фазовый портрет зависимостей плотности дислокации ρ, суммы параметров дальнего порядка ηo и количества вакансий Cv при различных начальных условиях.
Таким образом, кривые имеют параболический вид и траектория их движения похожа на часть фазового портрета для особой точки типа неустойчивого узла [7, 8].

.png&w=640&q=75)