Формирование траектории движения БПЛА при наземном мониторинге лесных экосистем на основе аппарата нечеткой логики

Применение беспилотных летательных аппаратов для мониторинга лесных экосистем на сегодняшний день является актуальным и одним из самых динамично развивающихся направлений использования беспилотных систем, как за рубежом, так и в России. С помощью беспилотной авиации можно в короткие сроки получать актуальные данные, которые помогают правильно оценить лесные запасы, выделить труднодоступные и непродуктивные насаждения, планировать лесозаготовки, определять породный состав и таксационные показатели древостоев, выявлять очаги распространения вредителей и болезней леса, противодействовать незаконной хозяйственной деятельности в лесах.

Весомые преимущества применения БПЛА делают привлекательными их как для авиационного, так и для наземного мониторинга лесных экосистем [2, с. 57]. Среди различных типов БПЛА наиболее перспективной альтернативой традиционным методам исследования местности является использование квадрокоптера.

Таким образом, целью работы является разработка алгоритма формирования траектории движения БПЛА при наземном мониторинге лесных массивов, включая автоматическое маневрирование для обхода препятствий, на основе аппарата нечеткой логики. В качестве препятствий рассматриваются «непроходимые» участки леса, состоящие из стволов деревьев и толстых ветвей.

Для выработки управляющих воздействий, позволяющих БПЛА огибать «непроходимые» участки лесного массива, в работе предлагается использовать систему нечеткого вывода типа Мамдани [1, с. 125].

Нечеткая модель управления движением БПЛА в трехмерном пространстве с целью обхода препятствий содержит пять входных лингвистических переменных Front (Впереди), Left (Слева), Right (Справа), Нigher (Выше), Below (Ниже) (рис. 1) и три выходных Rotation (Угол поворота), Нeight (Высота) и Velocity (Скорость).

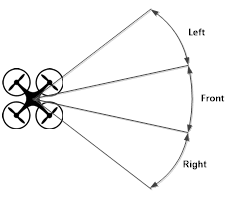
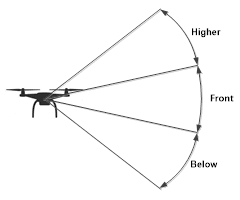
Рис. 1. Секторы анализа наличия препятствия

Каждая входная переменная соответствует сектору пространства по горизонтали или вертикали в направлении движения БПЛА, в пределах которых анализируется наличие препятствий и расстояние до них. Воздействие на выходные переменные позволяется БПЛА избежать столкновения с препятствием путем изменения угла поворота в горизонтальной плоскости (Rotation), высоты полета (Нeight) и скорости движения (Velocity).

В качестве терм-множества входных лингвистических переменных будем использовать множество T(Front, Left, Right, Нigher, Below) = {N (Near); M (Мiddle); F (Far)} с функциями принадлежности, показанными на рис. 2.

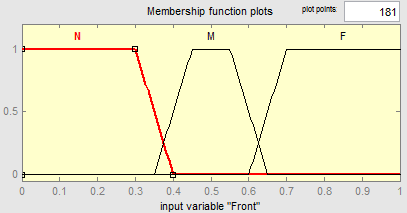
Рис. 2. Функции принадлежности входных лингвистических переменных

Терм-множества выходных переменных имеют вид:

T(Rotation) = {LB (Left Big), LS (Left Small), F(Front), RS (Right Small),

RB (Right Big)},

T(Нeight) = {UB (Up Big), US (Up Small), F(Front), DS (Down Small),

DB (Down Big)},

T(Velocity) = {ZV (Zero Velocity); SV (Slow Velocity); FV (Full Velocity)},

а их функции принадлежности приведены на рис. 3. Значения входных и выходных переменных даны в нормированном виде.

Исходя из логического анализа принципов обхода препятствий БПЛА при движении в трехмерном пространстве, сформирует нечеткую базу правил вида IF–THEN (табл. 1):

R^(l): IF x₁ is 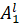 and ... and x_n is 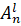, THEN y_n is , 

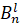где l=1,...,m, l – номер правила в данной нечеткой базе правил; 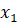, ...,  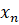– входные переменные, которые являются данными от датчиков подвижного объекта; 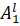, ...,  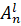– нечёткие входные множества;  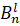– нечёткие выходные множества;  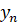 – выходные переменные.

Прочерк в ячейке табл. 1 означает, что значение этой переменной не учитывается в нечетком правиле. Во всех правилах в качестве логической связки для подусловий применяется только нечеткая конъюнкция (операция "И").

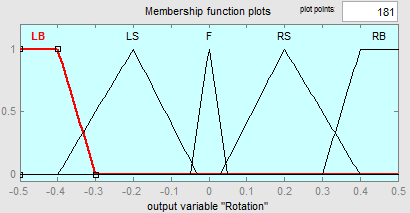
a)

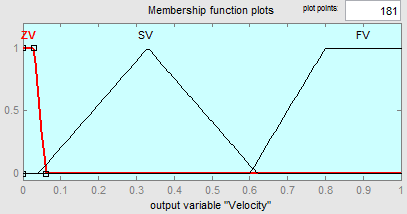
б)

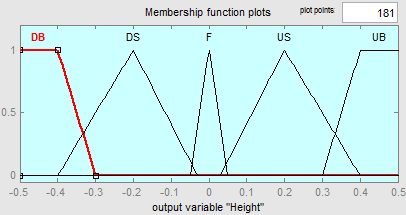
в)

Рис. 3. Функции принадлежности выходных лингвистических переменных Rotation (а), Нeight (б), Velocity (в)

Таблица 1

Правила продукций для нечеткой модели «Обход препятствий»

Для создания системы нечеткого вывода «Обход препятствий» воспользуемся средствами пакета расширения Fuzzy Logic Toolbox системы MATLAB [3, с. 163, 4, с. 451]. Графический интерфейс редактора FIS для системы нечеткого вывода типа Мамдани с пятью входными и тремя выходными переменными изображен на рис. 4, а графический интерфейс редактора правил после задания 19 правил нечеткого вывода из табл. 1 – на рис. 5. В качестве метода дефаззификации выберем метод наименьшего из максимумов (som), остальные параметры разрабатываемой нечеткой модели оставим предложенными системой MATLAB по умолчанию, а именно, логические операции над множествами (min – для нечеткого логического И, max – для нечеткого логического ИЛИ), метод импликации (min), метод агрегирования (max).

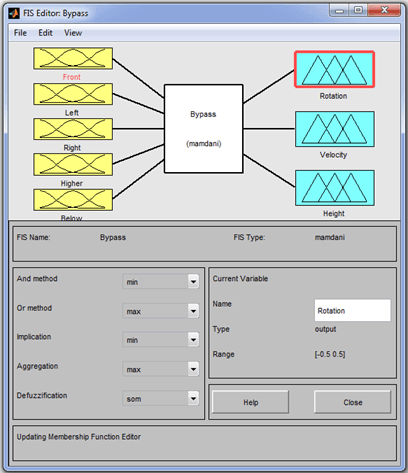
Рис. 4. Графический интерфейс редактора FIS для системы нечеткого вывода «обход препятствий»

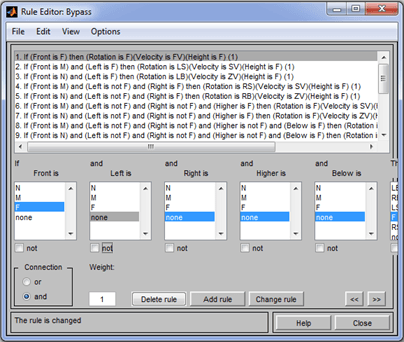
Рис. 5. Графический интерфейс редактора правил для системы нечеткого вывода обхода препятствий

Выполним анализ результатов поведения созданной нечеткой системы управления движением БПЛА для различных комбинаций входных переменных с помощью программы просмотра правил (рис. 6). Результаты сведены в табл. 2.

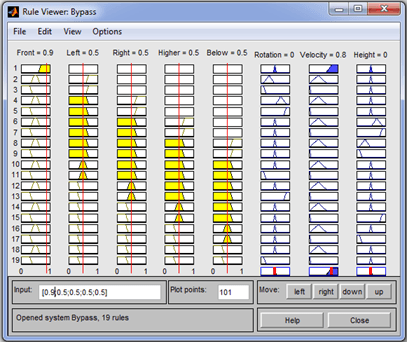
Рис. 6. Программа просмотра правил

Таблица 2

Анализ результатов поведения нечеткой системы управления движением БПЛА

Как следует из данных строки 1 табл. 2, в случае, если препятствие по ходу движения БПЛА (Front) находится на большом расстоянии (сектор свободен), то нет необходимости менять высоту и направление движения или снижать скорость.

Если препятствие впереди БПЛА обнаружено на среднем расстоянии и сектор слева свободен (строка 2 табл. 2), то необходимо снизить скорость до среднего значения и повернуть немного влево, не меняя высоты полета. Отрицательное значение переменной Rotation говорит о движении влево, положительное – вправо.

Если препятствие впереди БПЛА обнаружено на близком расстоянии и сектор слева свободен (строка 3 табл. 2), то необходимо снизить скорость до минимального значения и повернуть влево, не меняя высоты полета.

Аналогичное поведение БПЛА наблюдается в случае свободного правого сектора пространства (строки 4 и 5 табл. 2). При этом предполагается, что в секторах Front и Left наблюдаются препятствия на среднем или близком расстояниях.

Если сектора в горизонтальной плоскости (Front, Left, Right) содержат препятствия на среднем или близком расстояниях, а сектор Нigher – на большом расстоянии, то необходимо уменьшить скорость движения и увеличить высоту (строки 6 и 7 табл. 2). Увеличение высоты отображается положительным значением переменной Нeight, а уменьшение высоты – отрицательным значением.

Если сектора Front, Left, Right, Нigher содержат препятствия на среднем или близком расстояниях, а сектор Below – на большом расстоянии, то необходимо уменьшить скорость движения и уменьшить высоту (строки 8 и 9 табл. 2).

Если движение БПЛА происходит в условиях большого количества помех, то есть отсутствия свободных секторов, то движение будет направлено в сторону среднего расстояния до препятствия. Приоритет входных переменных соответствует рассмотренному выше для первых 9 правил: Front (наивысший приоритет), Left, Right, Нigher, Below (строки 10–18 табл. 2).

Если все сектора Front, Left, Right, Нigher, Below по ходу движения заняты препятствиями (строка 19 табл. 2), то БПЛА должен снизить скорость до нуля и выполнять повороты влево, пока не обнаружится свободный участок.

Таким образом, приведенные в табл. 2 результаты говорят об адекватности построенной нечеткой системы управления движением низколетящих беспилотных летательных аппаратов с целью предотвращения столкновения с препятствиями.