Генерация гексаэдрических сеток методом Sweep

В инженерном проектировании широко применяются различные математические пакеты и программные инструменты, позволяющие оценить качество конструкций на каждом этапе разработки. Такие инструменты позволяют анализировать динамику поведения проектируемого объекта и его кинематику, определять распределение температур и напряжений в механических составляющих. Эти задачи решаются с помощью средств анализа методом конечных элементов, в ходе которого происходит аппроксимация исследуемой области и деление ее на ячейки сетки для нахождения неизвестных величин [1, с. 65].

Целями данного исследования были изучение и описание алгоритма метода Sweep генерации гексаэдрических сеток для трехмерных B-rep моделей, а также реализация изученного метода на языке программирования C++.

Сетка конечных элементов – это разбиение заданной области на подобласти, которые называются элементами, так, чтобы каждая точка области находилась в одном из элементов. Вся область должна быть покрыта элементами без перекрытия, также должны выполняться условия совместимости между конечными элементами на границе.

На подобные сетки наложены такие ограничения, как отсутствие слишком больших углов (близких к 180 ^о), отсутствие слишком малых углов и ограничение размера конечных элементов (если по всей сетке используются элементы одинакового размера, необходимо выбрать достаточно малый размер, чтобы гарантировать достаточную точность в наиболее требовательной части области и при этом не повлечь за собой чрезмерно большие вычислительные требования).

Метод Sweep (метод заметания) – метод построения сеток конечных элементов, который позволяет строить расчетную сетку на основе призматических элементов с помощью операции протягивания элементов одного слоя вдоль некоторой оси. Данный метод может быть использован только для определенного класса геометрических моделей, полученных как тела вращения/протягивания.

Для построения сетки методом протягивания сеточных элементов геометрическая модель должна содержать поверхность-источник, элементы которой будут протягиваться вдоль некоторой оси в направлении поверхности-приемника. Данные поверхности изображены на рисунке 1.

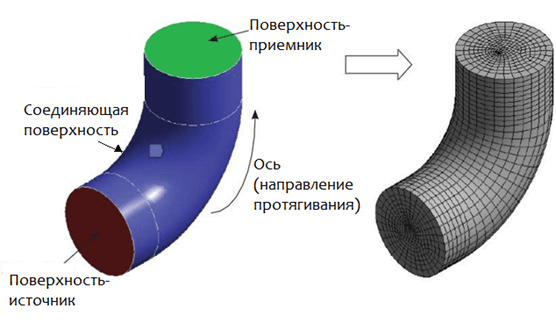
Рис. 1. Генерация гексаэдрической сетки методом Sweep

В результате работы метода получается структурированная или полуструктурированная сетка, состоящая из призм или гексаэдров.

Алгоритм методы Sweep в случае 1-to-1 заметания можно представить следующим образом:

1. Нахождение поверхности-источника и приемника, нахождение оси протягивания;
2. Создание четырехугольной сетки на поверхности-источнике (о методах создания таких сеток будет сказано далее);
3. Вычисление шага протягивания, то есть сдвига вдоль оси протягивания. В простейшем случае задается равномерное продвижение вдоль оси, но при наличии сильных изгибов лучше будет уменьшить шаг вблизи этих изгибов, чтобы повысить плотность гексаэдров, что, в свою очередь, приведет к более точной аппроксимации;
4. Размещение узлов на внешней поверхности тела;
5. Размещение внутренних узлов путем протягивания до сетки, расположенной на поверхности-источнике через тело с помощью аффинных преобразований: поворота, сдвига (данные операции рассмотрены далее в подразделе 1.8);
6. Соединений внутренних узлов друг с другом и с сетками на поверхностях, выделение гексаэдрических элементов.

Промежуточные шаги можно увидеть на рисунке 2.

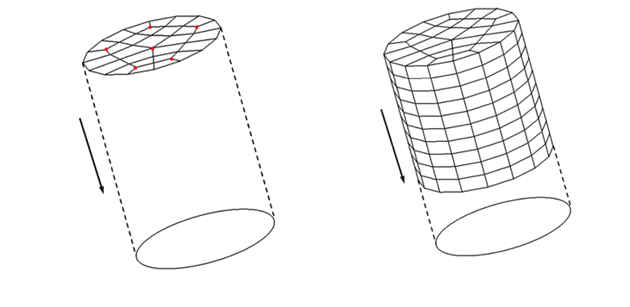
Рис. 2. Промежуточные шаги метода Sweep

Для генерации плоской сетки на поверхности-источнике можно воспользоваться методом трансфинитного отображения, либо методом Sweep для плоских фигур. Данные методы подробны описаны в [2, с. 81-83].

Для генерации внутренних узлов сетки необходимо переносить сетку, сгенерированную на поверхности-источнике, с помощью аффинных преобразований переноса на вектор и поворота. Более строго:

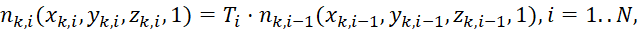 (1)

где n_k,i – набор внутренних узлов (первый индекс отвечает за номер точки в слое, второй индекс – за номер слоя);

T_i – матрица 4х4, композиция перемещения и поворота для заданной точки;

N – заданное количество слоев.

Вид и способ составления матрицы преобразования описаны в [5, с. 18-23].

У метода Sweep для генерации гексаэдрических сеток для трёхмерных B-rep моделей есть ряд основных преимущества, которые проявляются вне зависимости от поставленной задачи:

1. При его использовании получается малое, но достаточное для точной аппроксимации количество элементов сетки [3, с. 118];
2. Метод применим для любой 2.5D области (протянутой области);
3. При его использовании получаются элементы хорошего качества;
4. При применении адаптивного, а не равномерного шага вдоль оси протягивания, метод обеспечивает точную аппроксимацию в тонких геометриях;
5. Он эффективен по времени и памяти при генерации.

К недостаткам метода Sweep можно отнести:

1. Относительно небольшой класс областей, к которым применим метод (большое количество ограничений: топологическая эквивалентность сечений вдоль оси протягивания, прямая или приводимая к ней ось, отсутствие полостей внутри области и т. д.);
2. Существенное увеличение время работы алгоритма для случая N-to-M протягивания из-за применения алгоритмов структурной декомпозиции;
3. Малая точность аппроксимации в местах сильных изгибов (в классическом варианте алгоритма с равномерным шагом) [4, с. 84].

В ходе выполнения работы был реализован данный метод на языке C++ с использованием библиотеки Rhino 3D. На рисунках 3–5 можно увидеть результат работы программы на различных телах. Визуализация сетки выполнена в программном комплексе Ansys.

Рис. 3. Пример работы алгоритма

Рис. 4. Пример работы алгоритма

Рис. 5. Пример работы алгоритма

В результате проделанной работы был изучен метод Sweep (заметания) для генерации гексаэдрических сеток в трехмерном пространстве, изучены преимущества и недостатки метода, а также метод был реализован на языке программирования C++.