О проектировании толстостенных труб на основе четвёртой теории прочности

Основы теории расчета, зависимости для определения напряжений и деформаций толстостенных труб приведены, например, в [3]. При расчете толстостенных труб СПВ обычно применяется четвертая теория прочности (теория энергии формоизменения). Согласно этой теории, пластическое состояние наступает тогда, когда удельная энергия формоизменения достигает некоторого предельного значения. Рядом работ по исследованию упругодеформированного состояния металлов доказано, что эта теория прочности достаточно хорошо отражает условие пластичности в различных случаях приложения внешних сил [2].

Различают проверочный расчет и расчет при проектировании трубы [4].

Целью проверочного расчета является определение коэффициентов запаса прочности по различным сечениям ствола и сравнение их со значениями, рекомендуемыми нормалями и руководящими материалами. При таком расчете считаются известными кривая внутреннего давления в функции длины трубы, конструкция и материал трубы.

Целью расчета при проектировании является предварительный выбор наружной конфигурации трубы и (или) материала трубы. При этом считается, что внутренняя поверхности трубы конструктивно оформлена, известно распределение давления по длине трубы.

При проверочном расчете в каждом из выбранных сечений вычисляется величина предела упругого сопротивления трубы, которая по четвертой теории определяется выражением [2]:

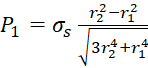, (1)

где

2×r₁ – внутренний диаметр трубы,

2×r₂ – наружный диаметр трубы,

σ_s – предел текучести материала.

Коэффициент запаса прочности:

,

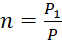где P – давление в трубе.

Для проектировочного расчета в [2] предлагается использовать зависимости:

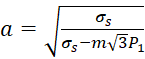,  (2)

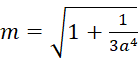,     (3)

.

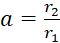В начале необходимо найти величину отношения a по зависимости (2) в первом приближении при m = 1, затем определить величину поправочного коэффициента по зависимости (3), и уточнить величину a по формуле (2) с полученным значением m.

Покажем, что на основе выражения (1) можно получить зависимость для вычисления a, не требующую уточняющих итераций.

В результате элементарных преобразований из (1) получим:

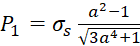.      (4)

Разрешив равенство (4) относительно параметра a, получим:

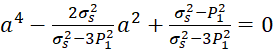    (5)

Равенство (5) представляет собой биквадратное уравнение [1]. Для z = a² будем иметь:

.

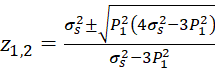Тогда корни уравнения (1) определятся выражениями:

,

.

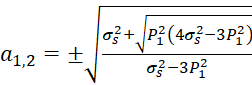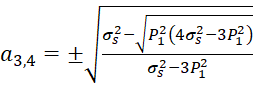Отбрасывая корни, не имеющие физического смысла, окончательно получим:

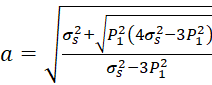.     (6)

Для сравнения результатов, получаемых по формулам (2), (3) и формулой (6), воспользуемся примером из книги [2].

Дано внутреннее давление на стенки трубы, P = 30 кг/мм². Требуется определить наружные размеры трубы, изготовленной из углеродистой стали (σ_s = 55 кг/мм²) при 2r₁ = 12 мм и n = 0.9.

По формулам (2), (3) в [2] получено a = 2,62 и 2r₂ = 31,5 мм.

По формуле (6) имеем:

,

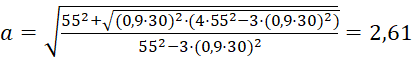2r₂ = 31,3 мм.

Полученные результаты расчетов близки, однако пользоваться формулой (6) удобнее, и она дает более точный результат. Использование формулы (6) позволит повысить эффективность процесса проектирования толстостенных труб.