Rationale for a new approach to post-quantum encryption

In today's world, we often need to transmit sensitive information over the internet. This can include passwords, personal data, and other confidential information that should never be accessed by third parties. Unfortunately, in 2019, there were 11,000 reported cases of personal data leaks in Russia, which is a 27% increase from the previous year. The average fine for violating personal data laws in Russia was 75,000 rubles in 2019. Rosstat [1] reported 1,087 information technology and communications-related crimes in 2020, with 1,017 of them involving unauthorized access to computer information.

This statistic may worsen as quantum computers become more prevalent. These computers perform electronic calculations much faster than conventional and supercomputers because they use three values (0, 1, and superposition) instead of two. Existing encryption methods need modification as they can no longer ensure information system security in their usual form. Before the advent of quantum computers, it was rational to use the same key to encrypt all messages in symmetric encryption. This was due to the fact that with this approach it was not necessary to exchange keys often, and hacking one such key using a conventional computer in a reasonable time was practically impossible for technical reasons: it required too much processor time and large amounts of Random-Access Memory (RAM) to sort through all possible combinations. However, the problems with processor time and storage of large amounts of data are not so acute for a quantum computer.

Thus, it becomes obvious that today the problem of information protection is quite urgent, therefore it is necessary to invent new encryption methods and modify existing ones, combining them to resist hackers who can use quantum computers for fast calculations.

To understand which method and how exactly it can be modified or combined, existing encryption methods and some post-quantum modifications of asymmetric encryption were reviewed and analyzed in detail.

For example, there is symmetric encryption. Symmetric algorithms provide high-speed encryption and decryption of data, since they use the same key for both operations [2, p. 74-78; 3; 4, p. 18-20], which means that only one key needs to be generated, and not, for example, a pair of keys, as happens with asymmetric encryption. In addition, the speed is achieved due to the fact that a symmetric encryption key usually has a relatively small length: from 128 to 256 bits [5, p. 164-167; 6, p. 6-9; 7, p. 30-31]. This makes it possible to process large amounts of information with minimal delays and overhead of processor time [8, p. 82-87]. The essence of symmetric encryption methods is to bring the message A_n to the form B_n on the sending side using a passphrase, and on the receiving side using a passphrase to bring the message B_n to the form A_n (pic. 1).

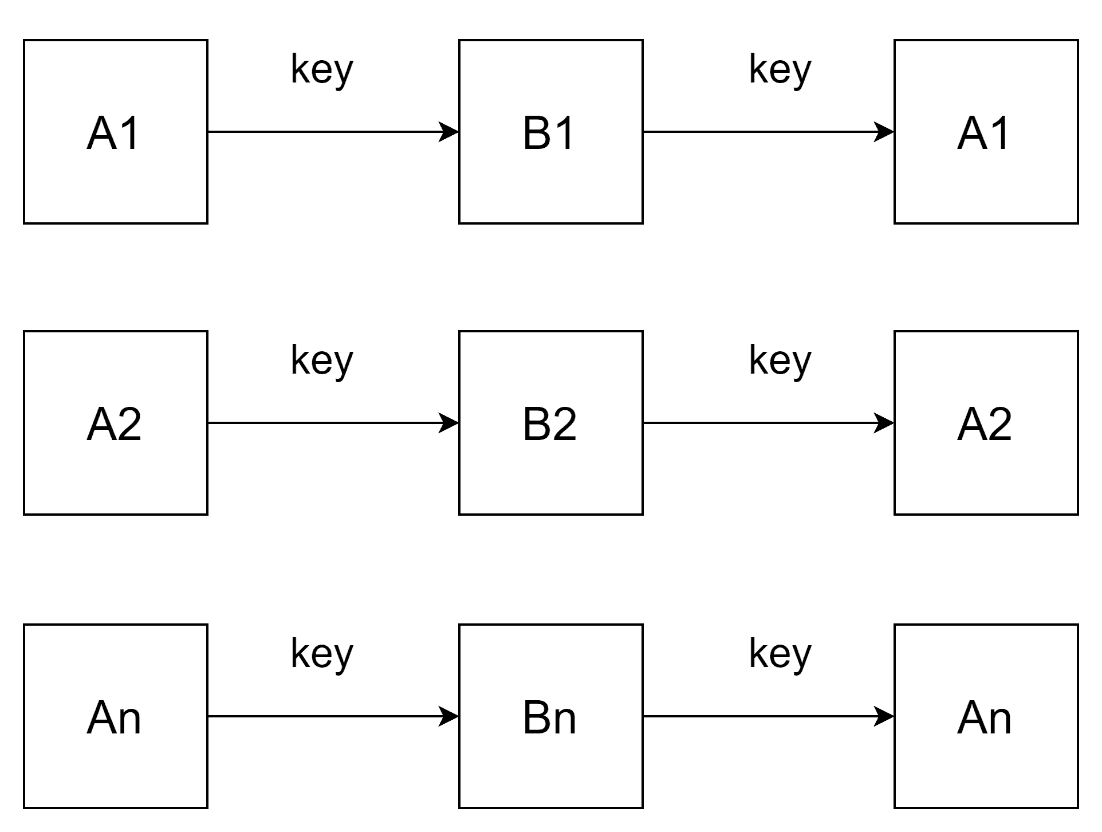
Pic. 1. The scheme of operation of the symmetric encryption algorithm

It is important to understand that the key is generated based on some keywords. In fact, it's just a set of characters, that is, a string, for example, "A keyword with complex characters &^* and numbers 123943, which is extremely difficult to crack by brute force." The longer the sequence of characters in a keyword, the better, because the more difficult it will be to find it by brute force. In this case, the key itself is a sequence of bits from 128 to 256 in length, depending on the specific encryption algorithm. The message A_n can also be anything, for example, a string "I love science." In this case, the message B_n is a sequence of characters incomprehensible to humans [9, p. 20-23], for example, "U2FsdGVkX1+WDKb95q2", which cannot be understood without decryption using the passphrase that was used for encryption on the sending side. The symmetric encryption process can be formalized as follows: imagine E_k as some encryption operator for which the following statement is true:

, (1)

where M is plaintext, C is private text, and k is the encryption key. That is, E_k maps plaintext to private text using the k key. Then the formula for the set of encrypted messages using symmetric encryption can be written as

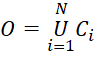, (2)

where O is the set of encrypted messages of some information system, N is the number of messages, C_i is an encrypted message (closed text) that was encrypted using the E_k operator.

Although this approach may seem promising, symmetric encryption algorithms pose a risk of compromising the key phrase. This phrase is distributed between conversation participants through various communication channels [10, p. 3-33]. Furthermore, this approach ensures that all messaging participants use the same key, simplifying the process of hacking. Only one key needs to be hacked, for example, through brute force, to decrypt all correspondence at once. The primary issue with hacking is that it can go undetected due to the lack of tracking tools. Unless the attacker reveals themselves by publicly using decrypted information, it is difficult to detect. However, from the hacker's perspective, it is more prudent to continue monitoring the communication channel after obtaining the secret key, rather than revealing themselves.

Therefore, it is evident that the use of symmetric encryption in its classical form is no longer rational with the emergence of quantum computers. This is due to the unreliability of communication channels and the need for frequent key changes.

To solve the problem of key compromise, an asymmetric encryption method has emerged based on the use of two keys: public and private. This method assumes that the private key is kept strictly confidential and is not shared among the conversation participants, while the public key is distributed to all participants. Asymmetric encryption algorithms utilize a private key exclusively for decrypting messages that have been encrypted using the corresponding public key. The process can be summarized as follows: Interlocutor A provides Interlocutor B with public key X. Interlocutor B uses key X to encrypt message M and sends the encrypted message MS to Interlocutor A. Interlocutor A decodes MS using private key Y to receive the original message M. Therefore, it is evident that this approach is superior to symmetric encryption. Each party possesses their own private key (Y), and the public key (X) can be safely transmitted over unsecured communication channels. This is because third-party interception of the public key does not pose any threat. It is important to note that the public key can only be used to encrypt a message, not decrypt it. The above reasoning explains the following formulas more clearly:

, (3)

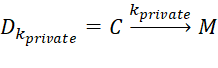, (4)

where E_kopen is the asymmetric encryption operator, k_open is the public encryption key, k_private is the private key, C is the encrypted message, M is the original message, D_kprivate is the asymmetric encryption decryption operator. Based on this, it becomes clear that the public key is used only for encryption, and the private key is used for decryption. In this regard, using an asymmetric encryption method is a more secure solution than using symmetric encryption algorithms.

However, this approach also has vulnerabilities. For instance, although it was previously believed that the public key could be sent without fear of interception, the advent of quantum computers has rendered the asymmetric encryption method, known as RSA, vulnerable to attacks. This is due to the Shore algorithm, which can be used to obtain a private key from a public key by solving the problem of finding prime factors of an integer.

In this regard, asymmetric encryption algorithms have been developed that are resistant to quantum computing. Among these, CRYSTALS-Dilithium, FALCON and SPHINCS+ can be distinguished, the essence of which is to use cryptographic methods based on solving problems of lattice theory or hash functions, the solution time of which does not differ on conventional and quantum computers. This is very reasonable, since Shore's algorithm cannot be applied to either lattice theory or hash functions.

However, the problem has not disappeared worldwide: the public key is still transmitted carelessly over open communication channels in the hope that it will not be possible to obtain the private key, but it is only a matter of time before an algorithm appears that can solve the problem of lattice theory or even hash functions. This is particularly relevant in the current era of rapid artificial intelligence development.

It is also important to note that asymmetric encryption is not a complete solution to the problem of information security, for the sole reason that asymmetric encryption is several orders of magnitude slower than symmetric encryption due to the longer encryption keys. Looking at the problem in more detail, it becomes clear that asymmetric encryption should be used as rarely as possible and only for specific purposes, such as transferring symmetric encryption keys.

Thus, it is obvious that existing encryption methods, including those considered to be resistant to quantum computers, do not allow reliable encryption of data transmitted via the Internet. In this regard, it seems relevant to formulate the task of developing such a method of information protection that will not have weak points or will have a minimum number of them and will ensure reliable encryption of information even in cases when a hacker attack is carried out using quantum computers.

A post-quantum encryption method has been proposed that does not include a public key, which makes it more secure against quantum attacks than asymmetric methods. For a more detailed consideration, it is necessary to introduce the following concepts:

• A message is a GET or POST request for the HTTP protocol.
• A client is a wrapper for an HTTP client that allows you to send HTTP requests using a user-friendly UI, that is, it can be a website or a mobile or desktop application.
• A server is a web application that accepts HTTP requests, processes them, and returns a response to incoming requests.

The essence of the method is to modify the symmetric encryption method. This modification proposes generating a new encryption key for each message, rather than using a single key for all messages. Each key can only encrypt and decrypt one message. Additionally, the encryption key must be generated using the same rule on both the client and server to avoid the need to send the key over communication channels.

In general, the modification of symmetric encryption has the form shown in Pic. 2. Here A₁, A₂, … A_n is the original message, B₁, B₂, … B_n is the encrypted form of the original message. In turn, key 1, key 2, ... key n is the key for message n.

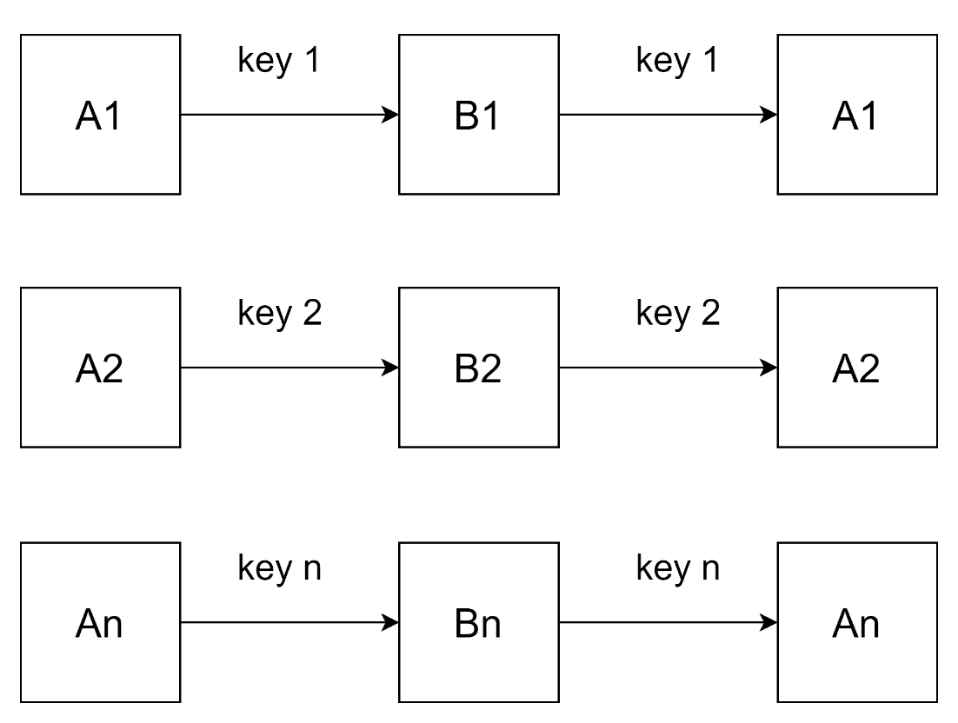
Pic. 2. The scheme of operation of the symmetric encryption algorithm

The formula for the set of encrypted messages of the symmetric encryption modification will have exactly the same form as formula (2) with one difference – each message uses its own k_i key to encrypt, that is, the operator is used:

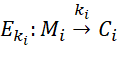 (5)

It is obvious that even if M₁=M₂=M_n, then C₁≠C₂≠C_n, because k₁≠k₂≠k_n.

For a more detailed understanding of the operation of this method, it is rational to consider a text messaging system that provides communication between users of the system, that is, a kind of messenger. The classic version of symmetric encryption involves creating an encryption key on the server and transmitting it to all system participants, i.e., clients. It becomes obvious that with this approach, two problems appear at once: first, the key can be intercepted at the moment of its transfer to clients; Secondly, a hacker needs to crack just one key, which is not a big problem if a quantum computer is used.

While the modification of symmetric encryption solves both of these problems, because the modification assumes that both the client and the server know how to generate the encryption key, which means that there is no need to transmit it over communication channels. Moreover, even if some key is hacked by brute force, the benefit from this from the hacker's point of view will be minimal, because this key will be able to decrypt only one message, which means it will be useless for other messages.

It was previously observed that the key is generated from a string keyword, allowing for a great deal of flexibility as the string can be generated based on a set of rules. For example, you can use the current time in the format "current day.current.month.the current year.the current hour. the current minute." Obviously, according to this rule, you can create a string on both the client and the server, because both of them can find out the current date and time.

Consider this example: User A wants to send a message to User B that includes a quote from Mikhail Vasilyevich Lomonosov: 'Mathematics should be studied because it puts the mind in order.' When User A clicks the 'Send message' button, the client application must create a keyword based on the aforementioned rule, receive a key, encrypt the message with this key, and transmit it to the server using HTTP or HTTPS protocol. Upon receiving the encrypted message, the server must generate a keyword using the same rule as the client, which takes into account the time to the minute.

In some cases, messages may be delayed due to prolonged communication channels. To address this issue, the program code can undergo various checks. So, for example, if it was not possible to decrypt the message according to the above rule, then you can try using the following rule: "the current day.the current month.the current year.the current hour. the previous minute." Similarly, we can assume that the message was sent at 12:59, and arrived on the server at 13:00, so the following rule should be provided: "the current day.the current month.the current year.the previous hour is 00." In addition, the message can be sent, for example, in 2023, and come to the server in 2024, for this you also need to provide a rule: "31.12.the previous year.23.59".

While this approach may appear reliable, it has a significant flaw. If any encryption key is compromised, all messages sent during that time period can be decrypted. Additionally, if a hacker studies the application's source code, hacking becomes an easy task. To mitigate these issues, it is recommended to personalize the keyword formation rule by adding unique information to messages generated for each user.

To do this, you can implement such a request on the server, which will return, for example, 10,000 random characters, which will be transmitted to the client using asymmetric encryption. At the moment, it is more reliable to use a post-quantum asymmetric method, for example, CRYSTALS-Dilithium, since it is invulnerable to the Shore algorithm. These 10,000 characters can be used to generate a keyword, for example, as follows: "10,000 characters. The current day. The current month. The current day. The current hour. The current minute."

Thus, each user will have a unique key even if the same date and time were used to generate it. This approach makes the algorithm invulnerable to hackers who know the source code of the software product. An attacker may see that the keyword is generated using the current date and time, but they will not be able to determine the 10,000 characters that precede the date and time.

Therefore, modifying symmetric encryption enhances security. Even if a secret key is selected through brute force, only one message can be decrypted.

It is important to note that this modification of symmetric encryption has the advantage that the software developer can implement the algorithm independently, improving security and performance by allowing for selective encryption.  For instance, consider a scenario where a user is requested to vote in an anonymous poll. The POST request would contain a unique survey ID and the number of the selected item. The message does not provide useful information to a potential hacker as it does not disclose the corresponding survey for this unique identifier. This information is classified and only accessible to the developer with database access. Therefore, encrypting this request is unnecessary. This can significantly improve performance for frequent or similar queries, particularly in mobile applications where it can also save battery power.

When considering this method, it is important to evaluate its effectiveness in comparison to other existing methods. For example, conventional symmetric encryption without constantly changing the encryption key and asymmetric encryption is both viable alternatives. The calculations used hypothetically possible hacker attacks as it would be too time-consuming to implement such testing in practice. Additionally, quantum computing was not considered due to its lack of availability at the time of the study.

A comparison was conducted on the time it takes to hack systems that implement different types of encryption: symmetric encryption with a 256-bit encryption key, asymmetric encryption with a 2048-bit encryption key, and the method proposed in this study (referred to as 'modification of symmetric encryption') with 256-bit encryption keys. The text describes two scenarios for hacking: using the Fugaku supercomputer, currently the most powerful in the world, and using a quantum computer. The calculations are designed to produce results within hours.

The performance of the Fugaku supercomputer is 442 petaflops. This means that it is capable of performing 442⋅10¹⁵ operations per second. Based on this information, it can be concluded that this supercomputer is able to crack a symmetric 256-bit encryption key in:

 (6)

hours. This number is greater than a billion years and even exceeds the age of the universe. This formula is explained as follows: the encryption key has a length of 256 bits, and the bit, in turn, can take one of two values: 1 or 0, which is why 2²⁵⁶ is written in the numerators, that is, one of two values can be in each of the 256 positions. The denominator records the number of operations that the Fugaku supercomputer is capable of performing in one second. This number was multiplied by 3600 to get the answer not in seconds, but in hours. That is, in general, this formula can be written as follows:

, (7)

where d is the key length in bits, k is the number of operations per second. With asymmetric encryption, at the time of writing, it is customary to use a key with a length of 2048 bits, which means that a supercomputer will need to crack such a key:

 (8)

hours. This number is also quite large; however, a quantum computer is able to decrypt much faster. For example, to crack a symmetric encryption key, a quantum computer with 150 qubits will only need:

 (9)

hours, which is about 3.5 days. This is still a large number, but this time can be considered quite reasonable, given the benefits that the hacker will receive. It is worth noting that the decryption rate with this approach increases in proportion to the number of qubits. For example, even with 160 qubits, a quantum computer is able to crack a 256-bit key in just 5 seconds. It is worth paying attention to the denominator in this formula. The number 3¹⁵⁰ means that 150 qubits are used, and each qubit can be in one of three states: in addition to 1 and 0, it can be in a superposition state. That is, in general, the formula can be written as follows:

, (10)

where d is the key length in bits, k is the number of qubits. Accordingly, to crack the encryption key with a length of 2048 bits, a quantum computer will need:

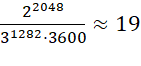 (11)

hours if 1282 qubits are used. However, even if there are 1290 qubits, such a key will be cracked in just 10.5 seconds.

It is evident that a quantum computer presents a significant threat to encryption keys of any size. This is because the number of qubits compensates for the length of the encryption key.

The use of symmetric encryption has been modified to significantly slow down the hacking process. This is achieved by multiplying the numerator by N, where N is the number of messages that need to be decrypted, in both the formula for cracking a 256-bit symmetric encryption key on a supercomputer and the formula for hacking on a quantum computer. Considering the potential volume of messages, such as hundreds of thousands per day, hacking would be considerably challenging even on a quantum computer with a high number of qubits. Thus, the Fugaku supercomputer will need:

 (12)

hours to crack all messages of an information system implementing a modification of a symmetric encryption algorithm. A quantum computer will need hours. And this is a pretty tangible result.

 (13)

Table shows the calculations mentioned earlier. The column 'Time spent hacking on a computer in hours' assumes that a computer refers to a Fugaku supercomputer.

Table

Comparison of hacking time for systems using different types of encryption

The name of the algorithm	Computer hacking time in hours	The time to hack a quantum computer in hours
Symmetric encryption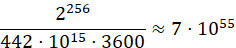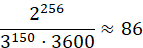
Asymmetric encryption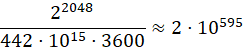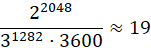
Modification of symmetric encryption

In conclusion, current methods offer a good level of protection against conventional computers and supercomputers, but they are vulnerable to quantum computers, which are able to crack encryption keys in a reasonable time. However, the modification of symmetric encryption proposed in this study offers much greater security than the use of symmetric encryption in its classical form, since the time taken to hack the entire information system is directly proportional to the number of messages, which can increase by millions every day if we are talking about a large social network, for example.

Based on the information received, a second conclusion can be drawn: a quantum computer with enough qubits can crack encryption keys in seconds, regardless of their length. However, the study suggests that there is still a significant amount of time before this becomes a reality. However, the proposed modification of symmetric encryption will only be effective until quantum computers become widely available with more than 150 qubits.

This study may also inspire other researchers to consider ways to protect against quantum computers with thousands of qubits.

1. Росстат. Официальная статистика. – Режим доступа: https://rosstat.gov.ru/folder/10705. (Дата обращения: 29.04.2023).
2. Берников В.О. Сравнительный анализ криптостойкости симметричных алгоритмов шифрования // Труды БГТУ. Серия 3: Физико-математические науки и информатика. 2020. № 1 (230). С. 74-78.
3. Бабенко Л.К., Ищукова Е.А. Криптографическая защита информации: симметричное шифрование // Учебное пособие / Сер. 11 университеты России (1-е изд.) Москва, 2018.
4. Горелик В.Ю., Трифонов Д.И., Матвеев М.В. Алгоритмы симметричного блочного шифрования // Автоматика, связь, информатика. 2019. № 11. С. 18-20.
5. Кочкаров Э.Р. Описание симметричного алгоритма блочного шифрования AES-128 // Тенденции развития науки: инновационный подход. Сборник материалов Международной научно-практической конференции. 2019. С. 164-167.
6. Шуваев В.В. Сквозное (оконечное) шифрование // Молодой учёный. 2019. № 6 (244). С. 6-9.
7. Чичикин Г.Я., Семёнов Д.А. Сквозное шифрование // Academy. 2019. № 5 (44). С. 30-31.
8. Алексеев К.А., Карнаухов Е.В., Сливинский В.Д. Сквозное шифрование и его применение в мессенджерах // Вопросы контроля хозяйственной деятельности и финансового аудита, национальной безопасности, системного анализа и управления. сборник материалов III Всероссийской научно-практической конференции. ФГБНУ «Аналитический центр» Минобрнауки России. 2018. С. 82-87.
9. Шабала М.Д. Исследование модификаций симметричного алгоритма блочного шифрования AES // Молодёжная научная школа кафедры «Защищённые системы связи». 2020. T. 1. № 2 (2). С. 20-23.
10. Al-Riyami S., Paterson K. Certificateless Public Key Cryptography // Advances in Cryptology - ASIACRYPT 2019. Lecture Notes in Computer Science. 2019. Vol. 11921. P. 3-33.