Development of Task Batch Execution Optimization System in Multi-stage Systems Using Branch and Bound Method

Introduction

The application being developed for optimizing schedules for executing batches of tasks in multi-stage systems using the branch and bound method is relevant, since existing methods allow one to find a solution, but they use exhaustive search algorithms, which leads to serious costs of both computational resources and time. The basis for optimizing this process is the branch and bound method, which helps to iteratively cut off unpromising optimization paths according to specified evaluation criteria, this allows you to reduce the amount of resources used and, accordingly, reduces the time spent on calculating and constructing an optimal schedule.

The subject of research is a system for optimizing the execution of task packages.

Practical significance of the work. The results of this work may be of interest to enterprises involved in the production or processing of products using a conveyor system.

Scientific and practical novelty. The developed system accumulates several stages of optimizing the execution of task packages using the branch and bound method, and also has a modular structure that provides flexibility for its implementation at various enterprises.

Objects and methods of research

Optimization problems arise in almost all areas of human activity. Each optimization task is the product of analysis and comparison with other (less desirable) activities.

Currently, optimization is used in the fields of science, technology and other areas of human activity. This includes, for example, the problem of planning production with maximum final profit for a certain amount of resources. The problem of managing a system of hydroelectric power plants and reservoirs at maximum power. The problem of space flight from one point in the universe to another, in the fastest way or with minimal energy consumption. The problem of quickly heating the oven to a given temperature and many other problems.

Optimization is a goal-oriented activity aimed at obtaining the best results under given resources and conditions.

It is worth reviewing the following concepts that will be considered and applied during the design and implementation of the solution.

A multi-stage system is a system in which the process of servicing each type of job (package) includes several processing stages (stages) on each of the devices. Thus, the system implements sequential processing of packets with the same routes on each device [1].

Job packages are a concept that implies the presence of several jobs of a specific type, performed without the need to reconfigure the devices of a multi-stage system to process jobs of a different type. A batch containing all jobs of the same type is called fixed.

A device is a mechanism that processes a unit of a job; the processing time of a job is fixed for each type; before processing a subsequent job of a different type, the device needs an n-th amount of time for changeover; changeover is not carried out when processing jobs of the same type or the so-called batch of jobs sequentially.

It is also worth noting systems that solve optimization problems.

From the existing classes of systems, the following global classes of systems can be distinguished:

• imitation;
• MES (Manufacturing Execution System);
• APS (Advanced Planning & Scheduling System).

Simulation systems

AnyLogic is a tool that allows you to simulate various processes, including conveyor systems, based on mathematical conclusions. This system provides clear visual diagrams with interactive display of the modeling process itself; with the proper skill, you can implement a mathematical model to optimize the production process. But this system does not allow the control of external production process systems, and also requires quite a lot of skill in designing and constructing mathematical models [2].

MES systems

MES systems operate within production conveyor processing enterprises, for example, in the HYDRA product, optimization is based on an evolutionary strategy or on production rules. HYDRA is a fairly powerful product that allows you not only to plan the production process but also monitors the states of devices and the amount of supplied resources. No matter how paradoxical it may sound, the disadvantage of this system is its complexity and implementation costs; this system must completely cover all stages and areas of production, which in turn is expensive both in terms of time and financial resources [3].

PHARIS is a unique MES developed by UNIS. PHARIS solves a wide range of problems and makes it possible to optimize a wide variety of production processes from creating a production order to planning, monitoring and production management, as well as documenting finished products and semi-finished products. PHARIS can also be considered as a manufacturing information system that provides an interface for interaction between injection mold control systems [4]. The PHARIS system is based on the use of genetic algorithms, 1C "Operational Production Management", on heuristic algorithms combining the use of greedy strategies and limited search strategies. This system is quite functional, but, like HYDRA, it is full-scale and suitable for global production enterprises with a high level of output and a large number of devices.

APS systems

APS systems are special in that they can be used both for planning and for optimizing discrete or continuous production. Examples of similar systems are SysQuest and ProMIRA. These systems are mainly used for planning the production process, taking into account the introduced restrictions, a schedule is built that will satisfy strict restrictions and will be acceptable so that the production time of the product is met, further optimization takes place taking into account the remaining non-rigid requirements. They do not guarantee finding the optimal schedule, and must also adapt to certain production systems.

The disadvantage of these systems is their focus on specific production enterprises or on production modeling, without the ability to adapt to various management system bases; such solutions provide planning and schedule processing systems taking into account given batches of products without the possibility of distributing the composition of these batches, since they are specified in static mode, this problem is partially solved by ASP systems that determine the installation of the required volume of products in strict system requirements. It is also worth noting that no open systems have been found that use the branch and bound method for constructing and optimizing schedules, so it was decided to design and implement a modular optimization system based on the branch and bound method, this will not only reduce the schedule planning time, but it will also allow integration of this system into any enterprise engaged in conveyor processing of products.

The proposed solution is the implementation of a system for optimizing the execution of batches of jobs in multi-stage systems using the branch and bound method, involves the calculation and construction of processing batches of jobs of ni types on n devices, taking into account the changeover to the execution of batches of jobs of a different type, each type of job has its own processing time per each of n devices, and also has a common changeover time for all devices for each of n types.

The system will have a modular structure, with the ability to replace modules as needed:

1. module for optimizing the composition of job packages;
2. module for optimizing the schedule for executing batches of tasks;
3. module for graphical presentation of the schedule.

The first module of the system deals with the construction and selection of the optimal composition of task packages depending on the specified number of tasks of each type.

The second module searches for the optimal schedule; the input of this module is the composition of task packages found after the first module.

The process of optimizing the schedule consists of finding an order for processing batches of jobs that gives the maximum estimate of the utility of the time spent completing the processing of all batches of jobs of each type; this estimate is taken based on the last device that will process the last batch of jobs. The maximum utility score is a score that reflects the minimum amount of time spent processing all job batches. To find optimal solutions, a breadth-first search strategy was used, with the preliminary exclusion of subsets that obviously do not contain optimal solutions. This is facilitated by the use of the branch and bound method, the study of each subset of solutions, which involves placing one package not included in the sequence of their execution in the current position. Elimination of a subset of solutions is carried out taking into account the comparison of the lower estimate for each branching level of the tree of variations of job packages; the iterative process involves considering branches whose lower estimate is minimal at a given level; there may be several such branches at the tree level. The construction of the final optimal schedule is carried out using a heuristic rule in which job packages are placed in descending order of changeover duration.

To further describe the algorithm in a formalized form, we introduce the following notation:

i – number of devices (conveyor segments);

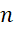– number of data types;

 – number of tasks of the i-th type;

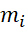– number of data batches i-th type ();

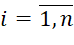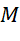 – vector of the number of task packages of each type;

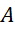– matrix of task package compositions;

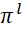 – sequence of execution of task packages on devices;

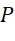– matrix of the order of processing batches of sequences;

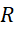 – data quantity matrixi -th type inj -th part of the sequence π^l;

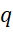– serial number of data inj -th part of the sequence π^l;

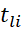 – duration of execution of tasks of the i-th type on the l-th device;

T – matrix of durations for performing tasks of the i-th types on devices;

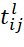 – duration of changeover of the l-th device from performing tasks of the i-th type to performing tasks of the j-th type;

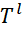– changeover matrices for l-th devices;

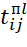– time points of the beginning of the implementation of actions from the i-th type BT in the j-th position in the sequence π^l;

 – matrices of the time instants of the start of execution of the BT of the i-th types in the j-th positions in π^l;

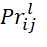 – downtime of the l-th device waiting for readiness to perform the i-th type of task, in the j-th position in the sequence.π^l.

A vector  and a matrix (where h corresponds to the number of the i-th type BT) represent input data specifying the number of packages of each i-th type (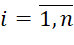) and the composition of these packages (total number of packages 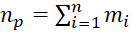. To formalize the type of sequences of BT execution in the MS, the matrix P is introduced in the consideration. The element 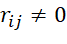, if the BT of the i-th type occupies the π^l j-th position, if the BT of the i-th type does not occupy the j-th  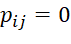position. In order to characterize the number of jobs of the i-th type () in packages occupying the j-th position in the sequences, the matrix R is introduced. Element, if the job of the i-th type occupies the j-th position with the number of elements in it equal to 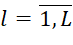 if the i-th type BT does not occupy  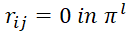j-th position. The order of BT execution on different MS devices is the same (the same types of sequences ()), therefore, when constructing schedules, one matrix P and one matrix R are formed. Then the schedule for BT execution on MS devices has the form: .

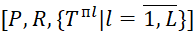To build a model of the process of executing a BT in a MS, a parameter was introduced into consideration, characterizing the downtime of the l-th device while waiting for the start of executing a BT of the i-th type, occupying the j-th position in (). There is no downtime of the (l=1)-th device waiting for the BT to be ready for execution: 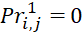 (, ). Downtime of each l-th device () while waiting for the readiness of the BT of the i-th type, occupying the (j=1)-th position in the sequences, are also equal to: 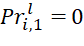. Downtime of the (l=2)-th, (l=3)-th and L-th devices waiting for readiness to execute the BT of the i-th type, occupying the (j=2)-th position in the sequences π², π³ and π^L, is determined by expressions of the form:

;

.

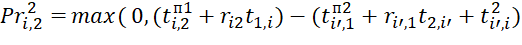Where i^' – the type of tasks, the package of which occupies the (j=1)th position in the corresponding sequences, – the number of tasks in the package of the i-th type, occupying the j-th position in [7].

Then the general formula for calculating downtime will be as follows:

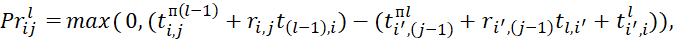  (1)

Where 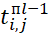 – the time point of the start of execution of the i-th type BT, occupying the j-th position in the sequence 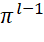(on the (l-1)-th device),  – the number of tasks in this package, – the start time of the start of the i’-th type BT execution, occupying (j-1)th position in the sequence π^l, 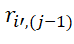 is the number of tasks in this package.

Values of the start time of execution of BT of i-th types in j-th positions () in the sequence 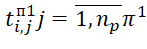(on the (l=1)th device) are determined by expressions of the form:

;

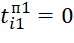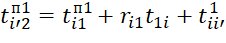
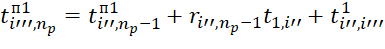    (2)

In accordance with (2), expressions for determining the values of 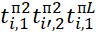, and 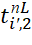moments of the start time of execution of the BT of the i-th and i'-th types, occupying the (j=1)th and (j=2)th positions in the sequences  and have the form:

(at), 

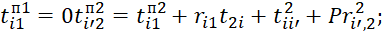
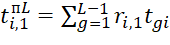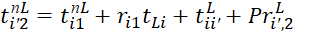,  (3)

In accordance with (3), expressions for determining the values ​​of, 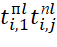have the form: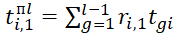

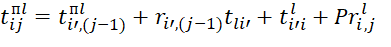 (4)

Where i'– the type of tasks, the package of which occupies the в π^l 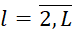 () (j-1)th position preceding the j-th position of the considered BT of the i-th type. Expressions (1), (2), (4) represent a mathematical model of the process of executing BT of the i-th types () on MS devices occupying the jth position in ().

To optimize the schedule for executing batches of tasks in MS using BBM, the following notations are introduced into consideration:

J – number of the current iteration of the branch-and-bound algorithm;

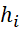 – identifier (number) of the i-th type BT placed in ();

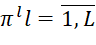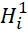 – sets of identifiers (numbers) of BTs of i-th types (), which were placed at previous iterations of the BBM algorithm in sequences ();

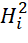 – sets of identifiers (numbers) of BTs of i-th types (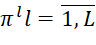), which were not placed at the previous and current iterations of the BBM algorithm in sequences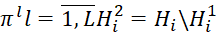

– a set of decisions on the order of execution of packages in the MS (schedules), in which . The th TB of the i-th type occupies the j-th position in the sequences  (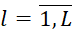) implementation of actions with them on system devices;

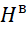 – uBTer estimate of criterion values f (record);

– lower estimate of the criterion values, calculated for the top of the tree corresponding to the ;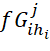

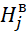– the maximum value of the criterion for admissible solutions for the order of execution of the BT corresponding to the sets, used to identify the upper estimate at the jth iteration of the algorithm .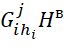

In accordance with the BBM, the j-th iteration of the algorithm is associated with the placement in the j-th position in sequences (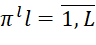) of various packets of the i-th types that were not placed in (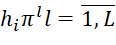) before the current iteration of the algorithm. Vertex with identifiersk_j  is associated with a set of solutions involving placement in the j-th position in sequences (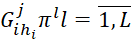) of oneh_i -th BT of some i-th type (), which was not placed before the current iteration of the algorithm [5-7].

The screening procedure involves 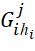, for all sets obtained as a result of the partitioning procedure, calculating the values of the lower estimates and  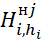comparing these values with the value of the current record . A set is eliminated 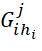 when the condition is satisfied for its lower estimate . In order to calculate the value for the corresponding set (vertex identified by the tuple), a matrix R is formed, each element  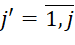 , where j is the number of the current position under consideration in 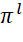(l=1,L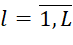) which corresponds to the number of tasks in the packages occupying the j'th position (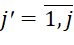). Identifiers of i job types and batch numbers are determined in the process of a depth-first traversal of the BBM tree from the root to the considered vertex (the formation of the matrix R is implemented in parallel with a depth-first traversal of the BBM tree from the root to the considered vertex). Based on the generated matrix R, the determination of the values of the time instants of the start of execution of the i-th types of BTs occupying the j'-th positions () in the sequences 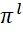 is realized. The calculation 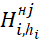of the lower estimate is carried out based on the value of the end time of execution of the i-th type of BT, added last to the considered (current) j-th position in the sequence 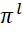(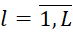), defined as follows: 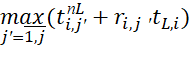. The method for calculating the lower estimate involves placing in the sequence (on the L-th device) following the task of the i-th type, occupying the j-th position, tasks of various i-th types (such that 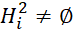) that remain unfulfilled.

The calculation of the initial value of the upper estimate (record) is based on the formulated method of ordering the i-th type of BT ().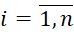

The calculation module of the application was tested, we will consider the option of constructing an optimal schedule, with the number of data types equal to 3, the number of data of each type equal to 8 and the conveyor length equal to 3. An example of data entry is shown in picture 1.

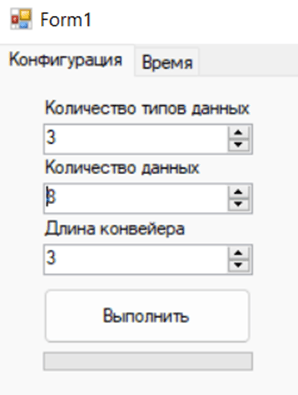
Pic. 1. Test data

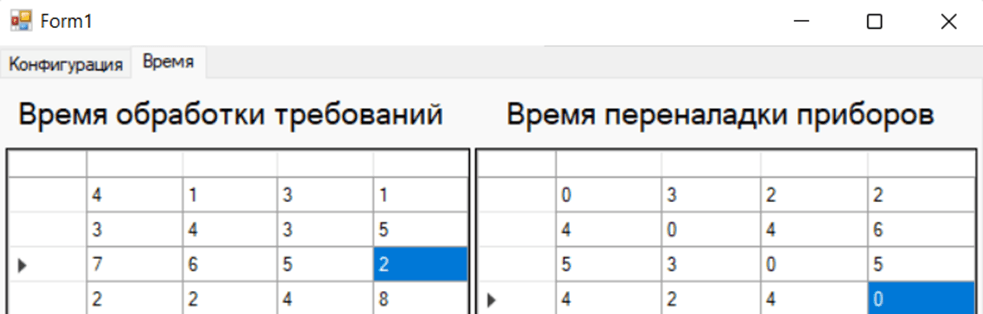
And also, in the «Время» tab we will set the matrix of package execution time for each data type, as well as the matrix of changeover time from one type to another. In the temporary processing duration matrix, the rows correspond to the device, and the columns correspond to data types. In the temporary changeover matrix, rows and columns correspond to data types, the changeover time from one type to the same type will be 0, since we do not changeover the device when executing one package of a specific type, accordingly, the changeover matrix will have 0 on the main diagonal of the matrix. The test data can be seen in picture 2. At this stage, we will set the matrix values in such a format so that there is compliance with the heuristic rule that arranges packages according to the duration of changeovers.

Pic. 2. Temporary matrix values for testing

Let us calculate the optimal composition and estimate the optimal schedule, picture 3.

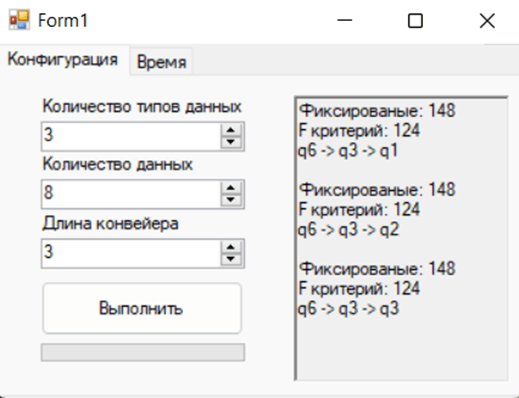
Pic. 3. Output of the result of calculating the optimal composition

An example of splitting job packages follows the following format according to the calculated indicators. The values in the chain q with the corresponding number are consistent with a certain partition of the packet, consider the optimal composition corresponding to q6–>q3–>q1, the composition for q1 will have the following format {3, 3, 2}, for q2 {4, 4} and finally for and finally for q3 {6, 2}, this is one of the options for splitting job batches to achieve an optimal estimate for the schedule.

For example, let’s increase the number of data types and the number of devices, and also edit the settings of the temporary matrices according to the following view, picture 4.

Pic. 4. Temporary matrices for the second testing

Let's launch the application. The calculation result for the current data is shown in picture 5

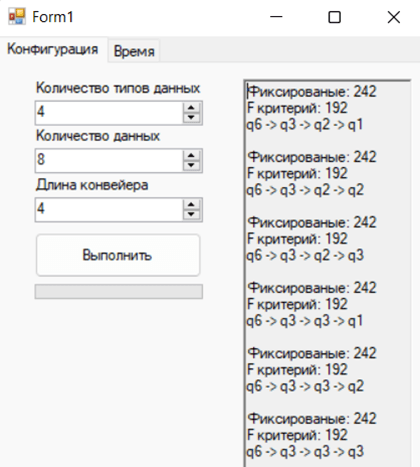
Pic. 5. Results of program execution during the second testing

As can be seen from the examples of such a distribution, the first partition is always a variation of packets having a partition q6 {3, 3, 2}, you can set such changeover indicators to change the priority, we will perform the setting according to the following form, picture 6.

Pic. 6. Changes in indicators of temporary matrices

The calculation results are shown in picture 7.

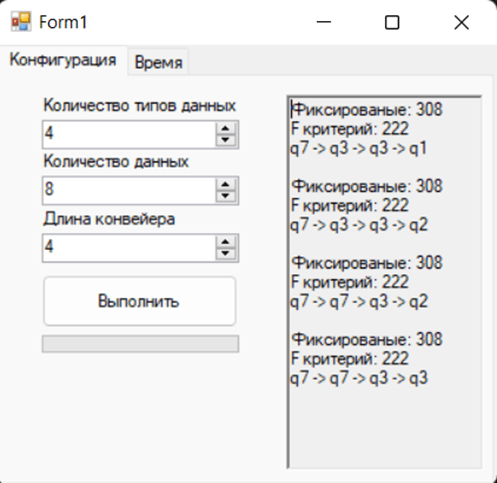
Pic. 7. Calculations when changing the values of temporary matrices

With this distribution of temporary matrices, you can see that the priority of choosing the partition of job packages has changed to q7, which corresponds to the following partition of the package {2, 2, 2, 2}.

To demonstrate the possibility of adapting the replacement of the visualization module, a module was developed that controls the Excel application window, which also visually displays the process of generating schedules, a fragment of the calculation interval is shown in picture 8, it is worth noting that the construction of schedules at each stage was carried out for a visual representation of the testing process, in the finalized version of the application the process of constructing variations will be used only to form one of the optimal composition options with numerical indicators for its evaluation.

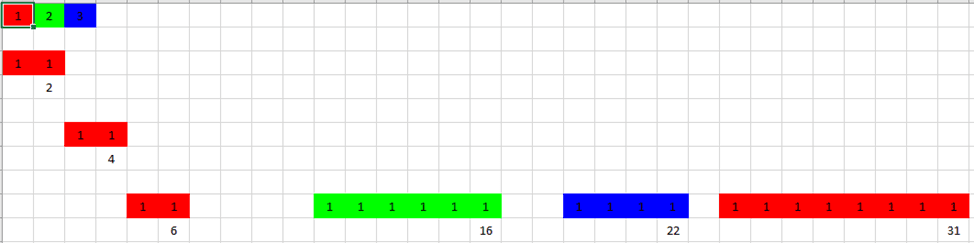
Pic. 8. Intermediate option for constructing a schedule and calculating an estimate

One of the options for the constructed schedule using the graphical Excel control module is shown in picture 9.

Pic. 9. Example of a built-in schedule using the Excel module

This example is more resource-intensive since managing the schedule rendering module takes up a certain amount of environment memory resources, and this library only provides access for cell-by-cell management in an Excel file, and each iteration of the output affects the calculation process too much and slows it down, for further testing in the profiling section, the rendering and graphical presentation module will be disabled to correctly assess the resources spent.

The Visual Studio development environment provides very powerful tools for profiling developed applications.

In picture 10 you can see a visual representation of the profiler in a graphical environment.

Pic. 10. Visual Studio profiling window

Let's launch the application and compare the resources spent when searching for the optimal schedule using the current solution, as well as exhaustive search, picture 11, the test was performed for 4 types, on 4 devices, with the number of data types equal to 8.

Pic. 11. Comparison of calculation results

At small values and with a small number of task packages, the number of types and devices, it is difficult to show the advantage of execution since the application itself and its graphical shell already occupy 25 MB of memory, so we will increase the number of data types to 6, the number of data to 16, and the number of devices to 5 and run the tests again, the execution result is shown in picture 12.

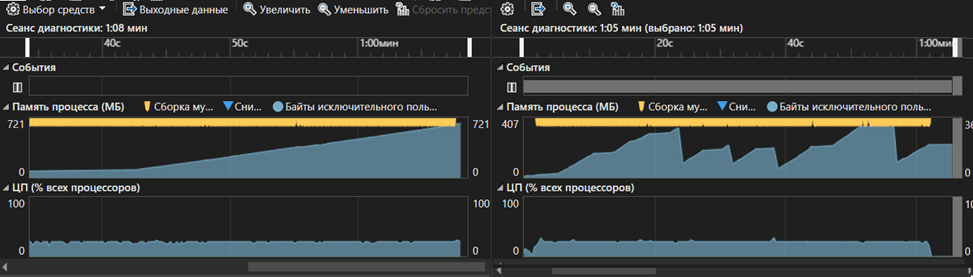
Pic. 12. Comparison of the current solution with a complete search using a large amount of data

Picture 12 shows a visual representation of the memory resources spent when calculating using exhaustive search (on the left) and the current solution (on the right), it is worth noting that the exhaustive search calculation began to fill the memory too quickly and did not even calculate the solution for the first subtree, which would correspond to a sharp a drop in occupied memory due to the «garbage collector», and in the figure on the right, during the same time, the current solution has already counted 4 subtrees, which is clearly visible from the corresponding jumps in occupied memory; it is also worth noting that the difference in peaks for each sub-tree is due to the cutting off of unpromising decisions.

Conclusions

A system was developed to optimize the scheduling of job batches in multi-stage systems using the branch-and-bound method.

The schedule was optimized by selecting the optimal composition of batches. The selection of optimal compositions was made using the branch and bound method, applying the evaluation criterion, which is the completion time of processing of all batches of tasks in the schedule, which was taken from the last device that completed processing its last task.

The work describes a process that includes stages of information search, containing the search for similar optimization solutions, as well as building a model based on it.

The system is implemented using a modular structure through aggregation of modules, which allows you to configure and replace modules responsible for the formation of trains, their division, as well as heuristic rules for the distribution of task packages when creating a schedule. The system contains a processing module, which is designed for communication with external systems or devices; in this work, an example is considered using a graphical module to display a schedule tree, as well as its extension for displaying a schedule using the Excel driver, which is part of the .Net framework.

Thus, we can conclude that the assigned tasks were solved, namely:

• the relevance of the solution to optimize the execution of task packages is substantiated;
• an analysis of existing solutions and their shortcomings was carried out;
• an algorithm for generating optimal batch compositions for constructing schedules is described;
• a system has been developed to optimize the schedule for executing batches of tasks;
• testing and analysis of the effectiveness of the current solution was carried out in comparison with exhaustive search.

The efficiency analysis was carried out by comparing the time and resource indicators of the system when performing calculations using the branch and bound method, as well as the exhaustive search method.