Одним из самых распространенных методов обработки данных в области медицины является регрессионный анализ. В данном типе анализа происходит определении аналитического выражения, в котором изменение одной величины обусловлено влиянием одной или нескольких независимых величин, а также множество всех прочих факторов, оказывающих влияние на зависимую величину.
Важным классом регрессионных моделей – деревья регрессии, которые позволяют осуществить разделение входного пространства на сегменты с последующим построением для каждого из них собственной модели и представить кусочно-заданную функцию регрессии в интуитивно понятной и наглядной форме.
Каждый шаг построения дерева регрессии с применением метода CART фактически состоит из совокупности трех трудоемких операций:
- сортировка источника данных по столбцу;
- разделение источника данных;
- вычисление индексов Gsplit для всех возможных разбиений.
Подсчет числа классов будет выполняться быстро, если знать число экземпляров каждого класса в таблице и при переходе на новую строку таблицы изменять на единицу только число экземпляров одного класса – класса текущего примера.
Все возможные разбиения для категориальных атрибутов удобно представлять по аналогии с двоичным представлением числа.
При одномерном ветвлении по методу CART деревья классификации при построении будут осуществлять полный перебор всех возможных вариантов одномерного ветвления. При данном условии будет найдено несколько вариантов ветвления, в которых будет присутствовать тот, который даст наилучшую классификацию.
Если имеется много предикторных переменных с большим числом уровней, поиск методом CART может оказаться довольно продолжительным, так же этот метод имеет склонность выбирать для ветвления те предикторные переменные, у которых больше уровней.
Для работы ИСППР для деревьев решений и для деревьев регрессии в задачах планирования с помощью машинного обучения по электронным персонифицированным картам данных больных требуется следующие данные:
- Фамилия, имя, отчество пациента;
- Пол пациента;
- Возраст пациента;
- Дата рождения пациента;
- Наличие очного посещения кардиолога или терапевта;
- Присутствие отметки об обращении за амбулаторной помощью;
- Вызовы скорой медицинской помощи;
- Наличие отметки о госпитализации в стационар, включающая в себя длительность лечения, дату поступления и выписки пациента, а так же количество дней проведенных в стационаре. Данный макет представлен на рисунке 1:

Рис. 1. Макет ИСППР для деревьев решений в задачах планирования с помощью машинного обучения по электронным персонифицированным картам данных больных
В анализе использовались данные персонифицированных счетов-реестров 2500 больных стенокардией, сделавших обращения за медицинской помощью в поликлиники, СМП (скорую медицинскую помощь) и стационары.
Работа с переменными для того, чтобы применить метод CART, показана на рисунке 2:
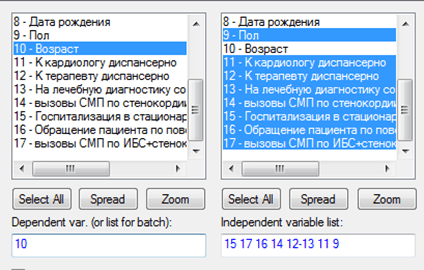
Рис. 2. Работа с переменными исходного набора данных
Дерево классификации для переменной «Возраст», использующее опцию полный перебор деревьев с одномерным ветвлением по методу CART сумело правильно классифицировать из 2500 значений 2496 значений.
Граф дерева для этого дерева классификации показан на рисунке 3.
В заголовке графа приведена общая информация, согласно которой полученное дерево классификации имеет 7 ветвлений и 8 терминальных вершин.
Терминальные вершины (листья) – узлы дерева, начиная с которых никакие решения больше не принимаются [5].
Началом дерева считается самая верхняя решающая вершина, которую иногда также называют корнем дерева. На рисунке она расположена в левом верхнем углу и помечена цифрой 1.
Первоначально все значения приписываются к этой корневой вершине и предварительно классифицируются, как 2 на это указывает надпись в правом верхнем углу вершины. Этот класс был выбран для начальной классификации потому, что число таких значений немного больше, чем других.
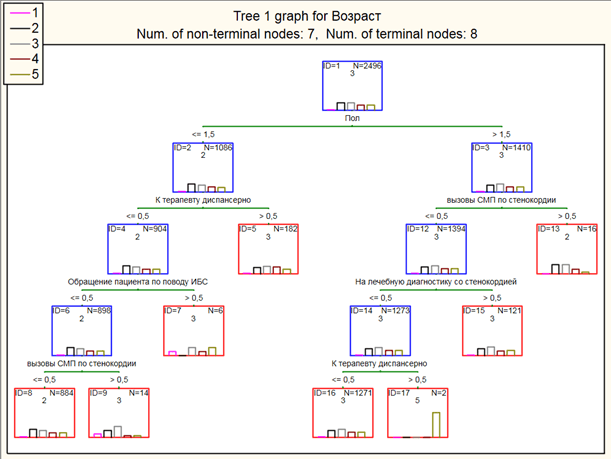
Рис. 3. Граф дерева для данной классификации
В левом верхнем углу графа имеется легенда, указывающая, какие столбики гистограммы вершины соответствуют значениям данной переменной.
Корневая вершина разветвляется на две новых вершины. Под корневой вершиной имеется текст, описывающий схему данного ветвления. Из него следует, что имеющие значение «Пол», которые меньше или равно 1,5, а таких значений 1086 отнесутся к вершине 2, а отнесенных к вершине номер 3 будут 1410 наблюдений, у которых пол больше или равно 1,5, то есть женщины.
Затем, если мы обратим внимание на вершину 2, то ее деление продолжится следующим образом. А именно, количество пациентов, которые обращаются «к терапевту диспансерно» составит 904 человека, а тех, кто не обратится 182 человека. Впоследствии те, кто не проигнорировал посещение терапевта, будут вынуждены, обратится по поводу осложнений, связанных с ИБС, и таких будет 898 человек. Те 6 человек мужского пола, которые обращались к терапевту, им окажется достаточно очного приема специалиста для уменьшения развития ИБС в стенокардию. Остальные 898 человек распределятся следующим образом: 884 человека вызовут скорую медицинскую помощь, так как у них наступит стенокардия, а остальные 14 человека не будут нуждаться в госпитализации.
Если рассмотреть ситуацию с женским полом, то есть разветвление вершины 3, то те, у кого были вызовы скорой медицинской помощи по стенокардии – их количество составит 1394 человека, а у 16 человек не было таких обращений, возможно, у них наличии ИБС без ведущих за собой осложнений в виде стенокардии.
Затем 1273 человека обратятся на лечебную диагностику со стенокардией, и затем эти же люди будут обращаться к терапевту за диспансерной помощью. У 121 человека не будет обращений на лечебную диагностику стенокардии.
Как видно из графа, проблемы с осложнением ишемической болезни в стенокардию наиболее чаще развито у женского пола, но при этом наблюдение и посещение специалистов, а так, же вызов скорой медицинской помощи практически всегда осуществляется у женщин. Мужчины реже обращаются на лечебные диагностики, что приводит к высокому значению вызовов скорой медицинской помощи.
На графе дерева вся эта информация представлена в простом, удобном для восприятия виде, так что для ее понимания требуется гораздо меньше времени.
Метод деревьев регрессии CART является удобным, если окажется правильный выбор варианта анализа. Чтобы построить модель, дающую хороший прогноз, в любом случае нужно хорошо понимать природу взаимосвязей между предикторными и зависимыми переменными.
Такой метод можно охарактеризовать, как набор иерархических, чрезвычайно гибких средств предсказания принадлежности наблюдений к определенному классу значений категориальной зависимой переменной по значениям одной или нескольких предикторных переменных [6].
Алгоритм обладает следующими преимуществами:
- алгоритм не является статистическим, поэтому не требует вычисления параметров вероятностных распределений;
- атрибуты разбиения выбираются непосредственно в процессе построения дерева, поэтому нет необходимости проводить процедуру отбора переменных для модели;
- алгоритм устойчив к выбросам и аномальным значениям;
- высокая скорость работы.
К недостаткам алгоритма можно отнести неустойчивость данных, а именно небольшие изменения в обучающем множестве порождают значительные изменения в структуре дерева решений.
Для оценки адекватности модели необходимо исследовать остатки [8].
Остатки должны иметь нулевое среднее значение и постоянную дисперсию, независимо от величин зависимых и независимых переменных, то есть быть нормально распределены. Модель должна быть адекватна на всех отрезках интервала изменения зависимой переменной. Вначале
На графике, который показан на рисунке 4 наблюдаемые значения, должны представлять приблизительно горизонтальную полосу одинаковой ширины на всем ее протяжении.
Коэффициент корреляции равен нулю между регрессионными остатками и переменными. Преобразование переменных или ввод новых, а также переход к нелинейной модели является основанием к применению, если возникает сомнение в адекватности модели, как например, если присутствует нелинейный тренд в регрессионных остатках.
Линейная модель регрессии предполагает, что переменные не взаимодействуют друг с другом, и изменение одного из них не оказывает никакого влияния на значения других.
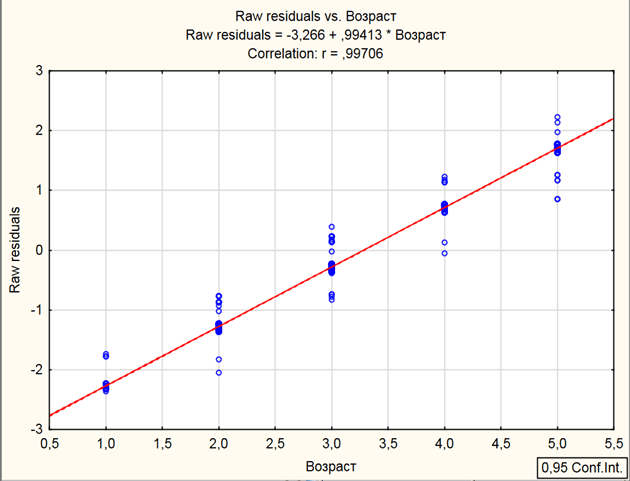
Рис. 4. График наблюдаемых значений зависимой переменной полученных по регрессионному уравнению

.png&w=640&q=75)