Justification of the mathematical model of mixed integer programming for optimizing scheduling of job packets

The scheduling of job packages in multi-stage systems is a complex task that often involves various constraints and limitations. In this article, we focus on justifying the implementation of a mixed integer linear programming (MILP) mathematical model for optimizing the schedules of job packages.

Methods

To address the challenges of scheduling job packages, we implemented a MILP mathematical model that takes into account the formation of result sets and the limitation of system functioning time intervals. As the problem of determining job package compositions and groups is NP-hard, we utilized approximate optimization methods. Additionally, we developed a method for constructing initial solutions for optimizing groups of job packages, as well as an algorithm for distributing job package execution results into sets within limited duration time intervals.

Results

The concept of program execution on a conveyor involves dividing it into fragments, each of which is assigned to a corresponding segment of the conveyor. The processing routes for all types of data are identical, strictly fixed, and involve passing through all conveyor segments. Let's introduce the following designations:

1. 𝑙 – the index of the conveyor segment ();
2. 𝑛 – the number of data types processed in the system;
3.  𝑖 – the identifier of the data type ;
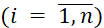4. nⁱ – the number of elements in the data set characterized by index 𝑖.

Data of the 𝑖-th type (𝑖 = 1, 𝑛) are processed by the corresponding program. The system uses 𝑛 types of programs processing 𝑛 types of data.

To form solutions for data batch compositions, the following notations are introduced:

1. 𝑚^𝑖 – the number of data batches of the 𝑖-th type 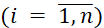, formed at the first decision-making level;
2. М – a vector corresponding to the quantities of data batches of 𝑛 types, formed from elements 𝑚^𝑖;
3. 𝐴 – a matrix, where the element 𝑎𝑖h represents the quantity of 𝑖-th type of data in the ℎ-th batch .

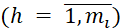The solution formed at the top level of the system hierarchy is represented as: [М, А], where:

1. М – a vector of the quantity of data batches of 𝑖-th types ;
2. А – a matrix of batch compositions.

In accordance with the solution for batch compositions, it is necessary to determine the sequence of their processing on the conveyor segments, the batch processing schedule. The batch processing schedule is denoted as 𝜋, representing a set of sequences 𝜋𝑙 for launching batches for processing on the 𝑙-th conveyor segments .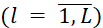

The schedule 𝜋 is formed assuming that the batch processing sequence is the same on all conveyor segments.

For the formalization of the sequences of 𝜋𝑙, the following is denoted:

1. 𝑃 – a matrix of the batch processing order;
2. 𝑝_𝑖𝑗 = 1, if the batch of data of 𝑖-th type occupies the 𝑗-th position in the sequence 𝜋^𝑙;
3. 𝑝_𝑖𝑗 = 0 if the batch of data of 𝑖-th type does not occupy the 𝑗-th position in the sequence 𝜋^𝑙;
4. The dimension of the matrix is 𝑛 × 𝑛_𝑝, where 𝑛𝑝 is the number of batches in the 𝜋^𝑙 sequences

Since the batch processing order is the same on all segments, it is sufficient to define a single order matrix 𝑃.

We introduce the matrix 𝑅 – the matrix of the quantities of data of the 𝑖-th types in the batches occupying the 𝑗-th position in the sequences 𝜋^𝑙 (𝑟_𝑖𝑗 – the quantity of data of the 𝑖-th type in the batch occupying the 𝑗-th position in 𝜋^𝑙 sequence).

Then, the solution formed at the lower level in the system hierarchy takes the form [𝑃, 𝑅].

For the formalization of the two-level decision-making model for batch compositions and their processing schedules in a conveyor system, the following notations are introduced:

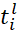1.  – the duration of processing data of the 𝑖-th type on the 𝑙-th conveyor segment ;
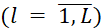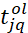2.  – the matrix of the start times of processing the 𝑞-th data in the batches occupying the 𝑗-th position in the 𝜋^𝑙 sequence , where 𝑛_𝑗 – is the quantity of data in the batch occupying the 𝑗-th position in 𝜋^𝑙 );
3. 𝑛_𝑝 – the number of batches formed at the top level of the hierarchy (the index of the last formed batch);
4. 𝑛_𝑛𝑝 – the quantity of data included in the 𝑛_𝑝-th batch (the index of the last data in the 𝑛_𝑝-th batch);
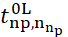5. – the start time of processing the last data in the batch with index 𝑛_𝑝 on the 𝐿-th conveyor segment.

Then, the time of completion of processing this batch on the 𝐿-th segment and the time of completion of processing all data in the system are determined by the expression:

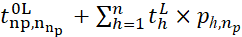 (1)

Therefore, the two-level model for determining effective batch compositions and their processing schedules takes the form:

1. the first (top) level: min 𝑓₁, where:

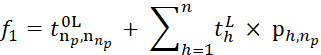
2. the second (lower) level: min 𝑓₂, where:

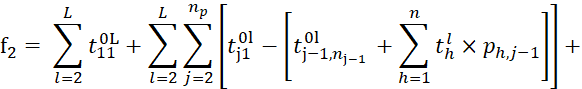
Thus, we have justified a two-level programming model for forming data batch compositions and their processing schedules in conveyor systems.

Conclusion

The study demonstrates that the proposed method, including the use of local optimization for group compositions, has shown promising results in increasing the number of formed result sets from task package executions in comparison to fixed groups. Furthermore, the dependence of scheduling efficiency on input parameters of the problem has been analyzed, providing valuable insights for optimizing job package schedules in multi-stage systems.