Очистка аудиосигнала от шума с использованием Вейвлет-преобразования

Введение

За последнее десятилетие был достигнут значительный прогресс в области обработки сигналов. Особенно новые методы обработки сигналов, такие как Вейвлет-преобразование, позволили исследователям решить разнообразные и сложные проблемы обработки сигналов.

Вейвлет-преобразование является мощным инструментом в области обработки сигналов, широко применяемым для удаления шума из различных сигналов. Одним из главных преимуществ вейвлет-преобразования является его способность разделять шумы от сигнала на различные уровни. Вейвлет-преобразование может быть применено к сигналам с различными типами шума. Оно эффективно устраняет белый шум, который проявляется как равномерное распределение мощности по всему спектру сигнала, а также импульсный шум и квазипериодический шум.

Кроме того, вейвлет-преобразование может быть реализовано в режиме реального времени, что делает его подходящим для различных приложений. Это позволяет удалять шум из сигналов в режиме реального времени, без предварительной обработки и оцифровки. Шум включает в себя все нежелательные окружающие звуки. Если звук воспринимается как приятная музыка или раздражающий шум, он будет восприниматься как имеющий тот же уровень децибел. Фундаментальным недостатком шума в аудиосигнале является то, что он ухудшает качество сигнала во время передачи по системе связи.

Распознавание сигналов с помощью вейвлет-преобразования включает в себя следующие этапы:

1. Сбор или получение сигнала, который содержит как желаемый сигнал, так и шум.
2. Выбор соответствующей функции вейвлета, которая соответствует характеристикам сигнала и шума. Различные вейвлеты имеют различные свойства, такие как время и частота локализации.
3. Применение Вейвлет-преобразование для разложения сигнала на различные частотные компоненты в различных масштабах. Это обеспечивает представление сигнала в области как времени, так и частоты.
4. Анализ коэффициентов вейвлета, полученных при преобразовании, и применение порога для подавления или удаления компонентов шума.
5. Выполнение обратного вейвлет-преобразования с использованием модифицированных коэффициентов для получения очищенного сигнала.

Вейвлет-преобразование позволяет точно идентифицировать и удалить компоненты шума, сохраняя при этом важные компоненты сигнала.

Реализация очистки аудиосигнала от шума в программе MatLab

Для реализации очистки аудиосигнала от шума в программе MatLab были сделаны следующие этапы:

1. Загрузка файла;

2. Добавление аддитивного белого гауссовского шума, так как исходный аудиосигнал чистый, чтобы увидеть процесс снижения уровня шума;

3. Найти длину аудиосигнала и определить некоторые параметры необходимые для подавления шума. Методом шумоподавления, используемый для определения пороговых значений шумоподавления для данных был выбран Bayes – эмпирический байесовский алгоритм. Этот метод использует пороговое значение, основанное на предположении, что измерения имеют независимые предварительные распределения, заданные моделью смеси. Поскольку измерения используются для оценки веса в модели смеси, метод, как правило, лучше работает с большим количеством выборок. По умолчанию для измерения риска используется правило задней медианы.

Пороговое значение действует для всех методов шумоподавления, но допустимые параметры и значения по умолчанию зависят от метода шумодавления. Для эмпирического байесовского алгоритма допустимыми параметрами являются Median, Mean, Soft или Hard. В этой работе был выбран мягкий порог (Soft).

Метод оценки дисперсии шума – это уровень шума, не зависящий от уровня шума (LevelIndependent). LevelIndependent – оценить дисперсию шума на основе вейвлет-коэффициентов наилучшего масштаба (с наивысшим разрешением).

Количество меток положения датчика – восемь, а в качестве вейвлета был выбран Симлет 8-го порядка (sym8).

4. Очистка аудиосигнала;

5. Сохранение файла.

[x,Fs] = audioread("Dance_Monkey.mp3");

xn = awgn (x, 15, 'measured');

xden = wdenoise(xn, 'DenoisingMethod', 'Bayes', 'ThresholdRule', 'Soft', 'NoiseEstimate', 'LevelIndependent', 8, 'Wavelet', 'sym8');

subplot (3,1,1)

plot(x);

title ('Исходный аудиосигнал');

subplot (3,1,2)

plot (xn, 'r');

title ('Зашумленный аудиосигнал');

subplot (3,1,3)

plot (xden, 'b');

title ('Очищенный аудиосигнал');

figure (2)

plot (xn, 'r')

hold on

plot (xden, 'b')

grid on

legend ("Зашумленный аудиосигнал", "Очищенный аудиосигнал")

hold off

здесь, xden – шумоподавленные данные;

xn – зашумленный сигнал;

DenoisingMethod – Bayes (по умолчанию)/BlockJS/FDR/Minimax/SURE/ UniversalThreshold.

ThresholdRule – Пороговое правило (James-Stein, Soft, Hard, Mean, Median)

NoiseEstimate – LevelIndependent (по умолчанию)/LevelDependent;

Level – Уровень вейвлет-разложения;

Wavelet – название Вейвлета.

Результаты исследования

Как исходный сигнал был выбран 15 секундный отрывок из песни «Dance Monkey», исполнителом является Tones and I. На этот отрывок был добавлен аддитивный белый гауссовский шум и очищен. Результат исследования можно увидеть на рисунке 1.

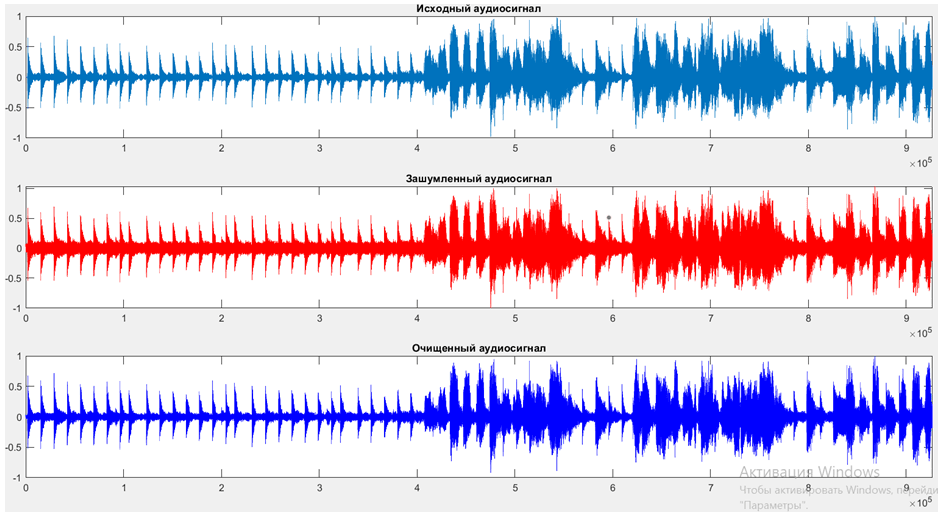
Рис. 1. График исходного, зашумленного и очищенного аудиосигнала

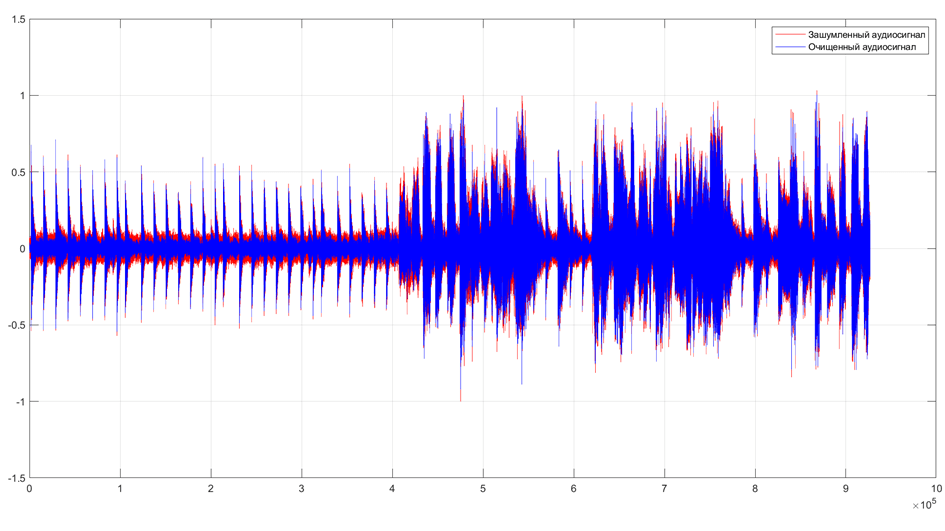
Рис. 2. График зашумленного и очищенного аудиосигнала

На рисунке 2 показано насколько хорошо был очищен аудиосигнал от аддитивного белого гауссовского шума, где красным цветом выделен зашумленный аудиосигнал, а синим очищенный аудиосигнал.

Заключение

Для анализа очистки аудиосигнала от шума был выбран 15 секундный отрывок из песни и туда же был добавлен аддитивный белый гауссовский шум. Для шумоподавления в аудиосигнале в системе компьютерного моделирования MatLab был выбран эмпирический байесовский алгоритм с мягким пороговым значением. В результате очистки аудиосигнала от шума с использованием Вейвлет Симлет 8-го порядка был получен исходный очищенный сигнал.

1. Dr.P.Senthikumar, Asha V, Dr.G.Ramesh, M.Muthukumar, Dr.Amairullah Khan Lodhi. An audio denoising approach using hybrid modified fast wavelet transform method. // International Journal of Trendy Research in Engineering and Technology. Volume 6. Issue 6. December 2022. ISSN NO 2582-0958.
2. Çiğdem Polat Dautov, Mehmet Siraç Özerdem. Wavelet transform and signal denoising using wavelet method. // IEEE. 2018.
3. Барышников П.В. Анализ методов очистки цифровых сигналов от шумов. // материалы Х Международной молодежной научной конференции. 2020. Том 3. С. 30-32.
4. Гапочкин А.В. Преимущество Вейвлет-преобразования в обработке речевых сигналов. // Вестник МГУП имени Ивана Федорова. 2015.