Применение обобщенных сетей радиально-базисных функций для решения задачи мягкой классификации

Мягкая классификация, в отличие от жесткой, подразумевает не только принятие решения о принадлежности поступившего на вход вектора информативных признаков к одному из возможных классов, но и формирование оценки вероятности принадлежности этого вектора к каждому классу. Ввиду значительной сложности этой задачи, во встраиваемых системах принятия решений часто аппроксимируют плотность распределения вероятности (ПРВ) как произведение независимых одномерных ПРВ каждого информативного признака (рис. 1 а), либо как изотропное распределение (рис. 1 б). Очевидно, что качество такой аппроксимации далеко не всегда удовлетворительно.

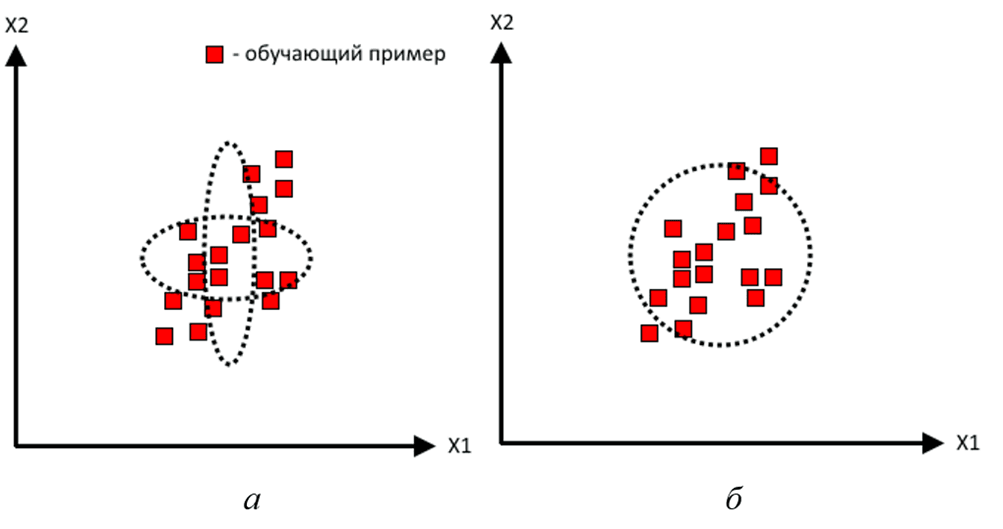
Рис. 1. Способы формирования упрощенной оценки ПРВ класса

Вполне естественным выглядит использование сетей радиально-базисных функций (РБФ). Сеть РБФ (рис. 2) – это нейронная сеть, нейроны которой используют радиальную функцию активации, т. е. их отклик на входной вектор информационных признаков зависит только от метрики расстояния этого вектора от центра функции нейрона. В классической сети РБФ функции активации нейронов одинаковы, отличаются только положения их центров в пространстве информативных признаков. Метрика расстояния, как правило, – евклидово расстояние, что делает функцию активации изотропной. В случае, если функция активации является гауссоидой (рис. 3), каждый нейрон сети РБФ отвечает за оценку вероятности того, что входной вектор – аддитивная смесь обучающего примера этого нейрона и гауссового белого шума (ГБШ).

Рис. 2. Устройство сети РБФ

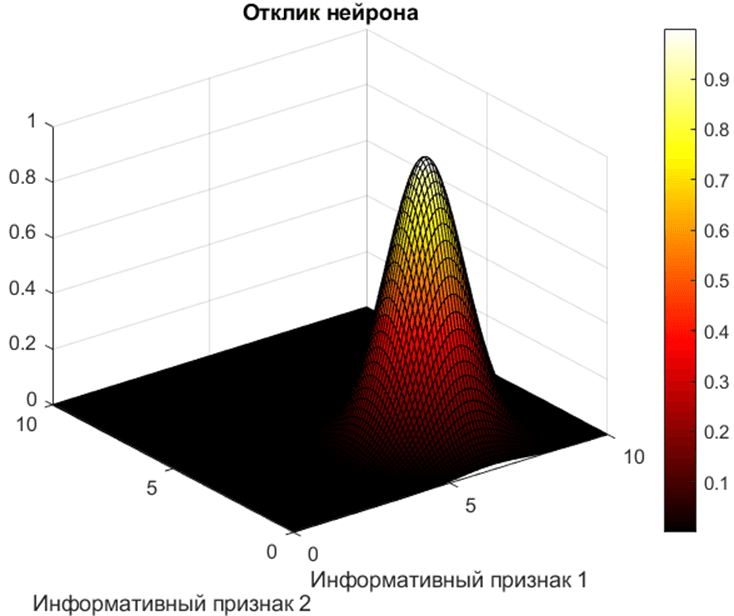
Рис. 3. Отклик нейрона с изотропной гауссовой функцией активации

Сеть РБФ организуется по принципу: каждому обучающему примеру соответствует собственный радиальный нейрон. Таким образом, подобрав плавность убывания функций активации, можно получить оценку ПРВ класса как сумму откликов всех нейронов, соответствующих обучающим примерам этого класса. Такой подход таит в себе неприятный недостаток. Дело в том, что обучающих примеров (и следовательно, нейронов) может требоваться очень много. Это приводит к риску переобучения сети, т. е. качество работы сети на новых, не входивших в обучающую выборку, данных будет низким. Именно как решение этой проблемы и появились обобщенные сети РБФ.

В обобщенной сети РБФ (рис. 4) нейроны соответствуют не отдельным обучающим примерам, а кластерам этих примеров, что радикально снижает их количество. При этом функции активации нейронов перестают быть одинаковыми. Теперь у каждого нейрона – своя уникальная эллипсоидально-симметричная функция активации, содержащая в себе информацию о ковариационной матрице нескольких обучающих примеров (рис. 5).

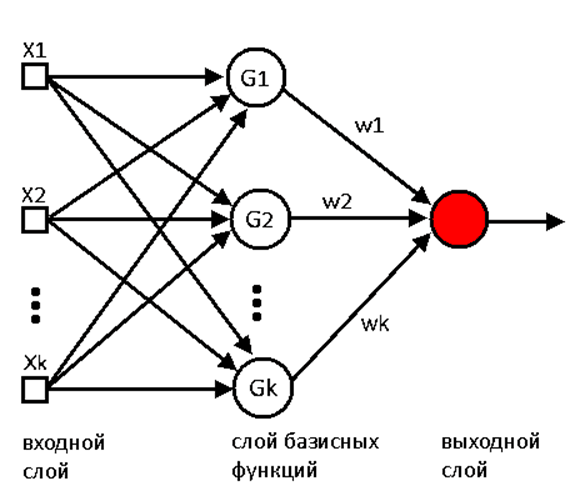
Рис. 4. Устройство обобщенной сети РБФ

Для двухмерного случая входной вектор х состоит из двух составляющих х₁ и х₂. Каждый обучающий пример, как и новые входные данные, является парой значений этих составляющих. Множество обучающих примеров в пространстве информативных признаков формирует сгустки произвольной формы (рис. 6), которые можно аппроксимировать либо эллипсоидально-симметричным распределением (рис. 5 а), либо суммой таких распределений (рис. 5 б) [1]. Каждое такое распределение задается по формуле:

 (1)

где  – оценка вероятности принадлежности вектора к данному классу,

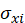 – среднеквадратичное отклонение i-ой составляющей в классе,

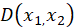 – матрица ковариации класса,

 – положение центра класса,

 – число обучающих примеров, из которых был сформирован класс.

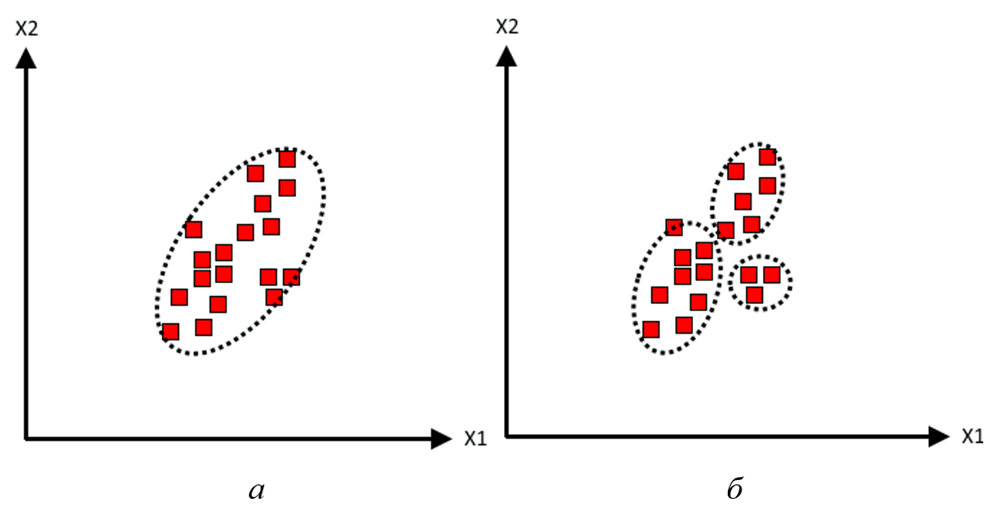
Рис. 5. Эллипсоидально-симметричные оценки ПРВ класса в целом (а) и отдельных участков класса (б)

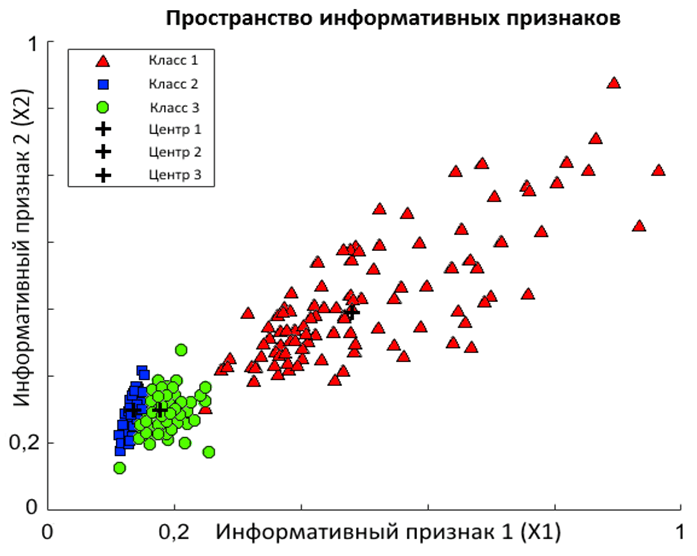
Рис. 6. Классы, сформированные по обучающим примерам

Таким образом, может быть легко получена оценка принадлежности вектора к классу, если вектор можно считать аддитивной смесью вектора центра класса и ГБШ. При этом задача заключается лишь в том, чтобы сформировать удовлетворительные оценки векторов центров классов и ковариационных матриц каждого класса. Один из способов формирования робастной оценки центра класса – взять центральное значение из среднего арифметического, медианы, центра и выборочного среднего интерквартильного диапазона, а также центра размаха (по каждой из составляющих вектора) [2, с. 250].

В результате отклик обобщенной сети РБФ на входной вектор – взвешенная сумма значений эллипсоидально-симметричных гауссоид каждого класса (рис. 7). Вес каждой гауссоиды при суммировании, очевидно, имеет смысл априорной вероятности класса.

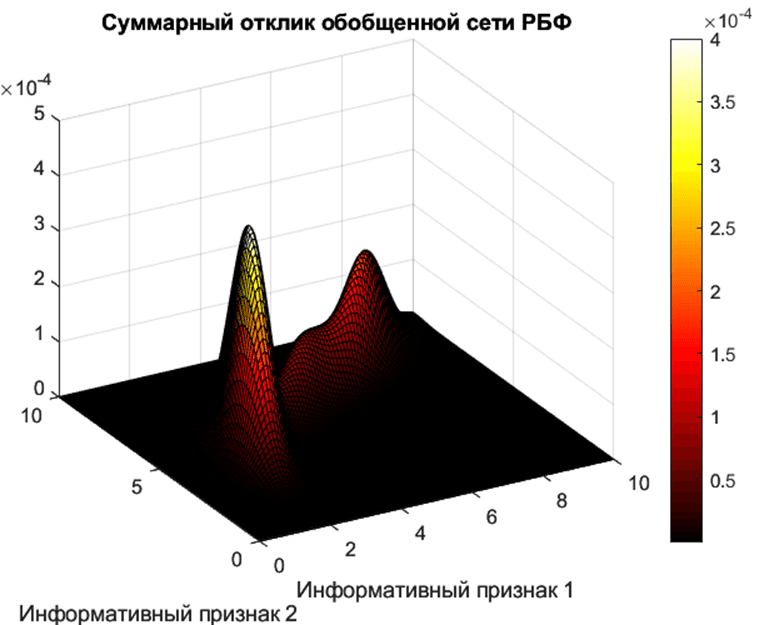
Рис. 7. Функция отклика обобщенной сети РБФ с тремя нейронами, соответствующими трем классам

Достоинствами подхода являются: более высокое качество аппроксимации по сравнению с изотропными и псевдомногомерными моделями; меньшее число нейронов, чем у обычной сети РБФ и отсутствие риска переобучения; возможность изменить число классов, просто добавив новые отдельно обученные нейроны этих классов. Основной недостаток – требуется большее количество операций при вычислениях, что вызвано обращением и умножением матриц в формуле 1.