Формулировка проблемы управления запасами заключается в необходимости обеспечить бесперебойное функционирование производственной или логистической системы при минимизации затрат, связанных с созданием и хранением запасов. Задачей стоит поиск стратегии нахождения оптимального баланса между двумя конфликтующими целями, первой из которых является поддержание уровня запасов, достаточного для удовлетворения потребностей производства или спроса клиентов. Дефицит запасов ведет к остановкам производства, срыву поставок, падению уровня продаж и потере репутации. Второй целью, в свою очередь, является минимизация затрат на создание и хранение запасов. Избыток запасов замораживает оборотный капитал, увеличивает затраты на хранение, риски порчи и устаревания товаров.
Иными словами, управление запасами предусматривает поиск ответов на два основных вопроса:
- Вопрос времени приобретения соответствующего товара;
- Вопрос размера заказа.
Началом периода активного исследования данных вопросов можно считать 1950-е годы, ознаменовавшиеся появлением первых математических моделей определения уровня страхового запаса и оптимального размера заказа. В частности, основы теории управления запасами в детерминированных условиях были заложены в работах К. Стефаника-Алмейера, К. Андлера и Ф. Харриса.
Однако, необходимо отметить, что функционирование реальных систем логистики и производства происходит в условиях неопределённости. Данные условия могут характеризоваться вариацией сроков поставки, колебаниями спроса, ненадёжностью поставщиков, различными издержками, возникающими в процессе транспортировки и хранения. Отказ учитывать приведенные факторы при определении ключевых параметров систем управления запасами чреват увеличением расходов на хранение избыточных запасов или, в ином случае, финансовыми потерями при их дефиците.
По этой причине, следующим этапом (с 1960-х годов) была начата активная разработка стохастических моделей управления запасами, которые учитывали случайный характер спроса и времени выполнения заказа. Публикации Дж. Хедли и Т. Уайтинга, а также Д. Бокса и Дженкинса стали знаковыми работами данного периода.
Современный этап исследований в данной предметной области характеризуется расширенным кругом факторов неопределенности и количеством разрабатываемых методов поиска оптимальных стратегий управления запасами. Особенно стоит обратить внимание на то, что с развитием информационных технологий появилась возможность собирать и обрабатывать большие объемы данных, описывающих динамику спроса и параметры поставок. В частности, ведутся активные исследования моделей управления запасами с учетом рисков колебаний цен, изменений валютных курсов, инфляций, банкротства контрагентов. Для поисков оптимальных решений используются методы стохастического программирования и имитационного моделирования, теория массового обслуживания, эвристические алгоритмы оптимизации.
Актуальность исследований в данной области обуславливается возрастающей сложностью глобальных цепей поставок, общим повышением уровня рыночной нестабильности, появлением экономических угроз (примером может послужить пандемия COVID-19), а также ряд иных масштабных политико-экономических процессов, последствия которых имеют особое значение в контексте современной России.
Потому целью исследования стоит не только более глубокое изучение существующих моделей и стратегий, но и разработка модели управления запасами с учетом случайности спроса и ненадежности поставщиков.
Методы решения задачи управления запасами подразделяются на детерминированные и стохастические. В детерминированном случае задачи управления запасами предполагается, что все параметры модели, в частности спрос, время поставки, затраты - известны и постоянны. В этом случае поиск оптимальной стратегии управления может считаться достаточно тривиальной задачей. Далее будут перечислены основные модели и методы решения детерминированных задач управления запасами:
- Модель экономичного размера заказа (EOQ – Economic Order Quantity). Определяет оптимальный размер заказа, минимизирующий суммарные затраты на оформление заказов и хранение запасов, при известном постоянном спросе и мгновенном пополнении запасов.
- Модель производственного размера партии (EPQ – Economic Production Quantity). Является модификацией EOQ для случая, когда пополнение запасов происходит не мгновенно, а с определенной интенсивностью.
- Модель планирования дефицита (Planned Backorder Model). Допускает возможность планового дефицита с последующим исполнением отложенных заказов. Минимизирует общие затраты с учетом потерь от неудовлетворенного спроса.
- Модель с учетом оптовых скидок (Quantity Discount Model). Учитывает возможность получения скидок при заказе больших партий товара. Определяет оптимальный размер заказа с учетом оптовых скидок.
- Модель с ограничением на размер заказа или емкость склада. Находит оптимальные параметры стратегии управления с учетом дополнительных ограничений на максимальный размер партии или вместимость хранилища.
- Модели с учетом временной стоимости денег. Минимизируют приведенную стоимость общих затрат на управление запасами за определенный период планирования.
Для решения детерминированных моделей используются методы классической оптимизации (нахождение экстремумов функций, решение уравнений), динамическое программирование, различные эвристические алгоритмы.
Важно заметить, что несмотря на относительную простоту, детерминированные модели управления запасами служат основой для разработки более сложных моделей, учитывающих факторы неопределенности.
Двигаясь в сторону усложнения, далее предлагается рассмотреть стохастические методы решения задач управления запасами, учитывающие факторы неопределенности, среди которых случайный спрос, где размер спроса на каждом периоде является случайной величиной с известным законом распределения; Случайное время задержки поставки; Случайный объем поставки, где фактический размер полученной партии может отличаться от заказанного и быть случайной величиной; Неопределенность цен и затрат; Неполнота информации о вероятностных характеристиках спроса; И последним, на что в рамках исследования следует обратить особое внимание, будет ненадежность поставщиков, фактор, определяющий наличие вероятности срыва поставки заказанной партии.
Основные методы решения для стохастических моделей включают аналитические методы, методы стохастического динамического программирования и стохастической оптимизации, имитационное моделирование, эвристические и приближенные методы.
Далее, предлагается рассмотреть методы решения неопределенного варианта решения задачи управления запасами:
- Модель критического уровня (точки заказа) с фиксированным размером заказа (R, Q): Заказ размером Q размещается каждый раз, когда уровень запаса достигает критического уровня R. Основные параметры стратегии: R – минимально допустимый запас, ниже которого подается заказ, и Q – постоянный размер заказа.
- Модель с фиксированным интервалом времени между заказами и фиксированным размером заказа (T, Q): Заказы размером Q размещаются регулярно через фиксированный интервал времени T. Основные параметры: T – периодичность размещения заказов и Q – постоянный размер заказа.
- Модель критического уровня с двумя уровнями запаса (R, r): Заказ подается, когда уровень запаса достигает критического уровня r, и пополняется до максимально желательного уровня R. Параметры: R и r – два критических уровня запаса.
- Модель с периодической проверкой запаса и пополнением до максимального уровня (T, S): Фактический запас проверяется регулярно через интервал T. Если запас упал ниже S, размещается заказ на количество до уровня S. Параметры: T – периодичность проверок, S – максимальный целевой запас.
- Модель с периодической проверкой запаса и возможностью дефицита: Схожа с (T, S), но допускается наличие дефицита на момент проверки. Заказ размещается для пополнения запаса до S.
- Модель с непрерывным контролем запаса, случайным временем задержки поставки и возможностью дефицита: Непрерывный мониторинг запаса. Время между заказом и поступлением партии – случайная величина. Допускается дефицит до прихода заказа.
- Модель газетчика: Непрерывный контроль запаса, мгновенное пополнение поставок. Спрос случаен, допускаются дефициты. Минимизируется сумма затрат на заказ, хранение и штраф за дефицит.
- Модель с непрерывным контролем запаса и случайным временем задержки поставки: Непрерывный мониторинг запаса. Время между заказом и поступлением партии является случайной величиной. Цель – минимизация общих затрат.
- Модель при случайном спросе и ненадежных поставщиках: рассматривается несколько альтернативных ненадежных поставщиков с вероятностями срыва поставки. Спрос случаен. Цель – оптимальный выбор поставщиков и стратегии управления запасами для минимизации затрат.
Особое внимание следует обратить на последний пункт: в нынешних реалиях фактор ненадежности поставщиков особенно интересен, и учетом общемировой нестабильности рынков, именно изучение и построение точной и надежной модели решения задачи управления запасами при случайном спросе и ненадежных поставщиках может оказать мощное положительное влияние на функционирование отечественного бизнеса [1, c. 148].
Предлагается рассмотреть задачу оптимизации управления запасами при случайном спросе и наличии альтернативных поставщиков с разными уровнями надежности. Предлагаемая модель может найти применение при выборе поставщиков на тендерах, а также при оперативном управлении поставками на основе теоретического обоснования.
Приведем исходные положения, необходимые для построения модели оптимального выбора стратегий управления запасами с учетом случайности спроса и ненадежности поставщиков [3, c. 115].
Рассмотрим однономенклатурную систему управления запасами в дискретном времени на периоде планирования T = Nt, где t – период контроля состояния запасов. Моментами принятия решений о размере заказов являются дискретные моменты времени tk = kt, k = 1, 2, …, N – 1. Правилом оценки эффективности системы предлагается выбрать критерий минимума суммарных средних затрат (затраты на пополнение запасов, затраты на хранение и потери вследствие дефицита) на периоде планирования T [2, с 288]. Возьмем интервал длительности t – шагом процесса управления. В начальный момент каждого шага измеряется значение фиктивного уровня запасов x. После, основываясь на результатах измерения принимается решение о необходимости подачи заказа на пополнение запасов (который поступит в систему через случайное время q) и размере заказа u.
Спрос на k-м шаге описывается случайной величиной zk. Предполагается независимость случайных величин в совокупности, и наличие одинакового вероятностного распределения с функцией распределения F(z) с плотностью вероятности f(z).
Затраты на пополнение запасов в размере u связаны с подачей заказа одному из поставщиков множества M. Затраты для j-го поставщика описываются функцией (1):
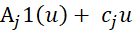 (1)
(1)
Где Aj – фиксированная часть затрат на j-го поставщика, 1(u) – функция единичного скачка, равная 1 для положительных u и 0 для прочих, cj – закупочная цена единицы продукции у j-го поставщика. Предполагается ненадежность поставщиков, с возможностью полного срыва поставки pj j-м поставщиком, и вероятностью обеспечения поставки 1 – pj. Считается, что поставщик, сорвавший пополнение запасов, не получает платы. При срыве поставки заказ тут же передается другому поставщику. Значит, каждый из поставщиков характеризуется тремя значениями – Aj, cj, pj.
Построим модель оптимального выбора размера поставки в условиях случайного спроса и ненадежности поставщиков.
Первым этапом введем концепцию обратного дискретного времени – это концепция, используемая в области анализа и обработки сигналов, описывающая процесс анализа данных или сигналов в обратном порядке по времени. В контексте обратного дискретного времени данные анализируются или обрабатываются, начиная с последних доступных наблюдений и двигаясь к более ранним.
Выдвинем предположение: за n шагов длительности t до конца периода планирования, фиктивный уровень запаса в системе равен x и происходит принятие решения формирования заказа размером u. В таком случае средние затраты на каждом шаге между моментами в обратном дискретном времени tn и tn–1. Они составят (2):
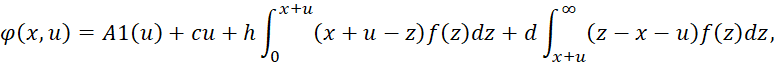 (2)
(2)
При введении функции минимальных средних затрат для процесса, длительностью n-шагов, начинающегося с фиктивного уровня запасов x, обозначив ее 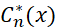 , можно сделать вывод, что данная функция удовлетворяет уравнению дискретного динамического программирования следующего вида (3):
, можно сделать вывод, что данная функция удовлетворяет уравнению дискретного динамического программирования следующего вида (3):
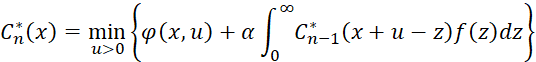 (3)
(3)
Где начальное условие имеет вид (4):
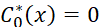 (4)
(4)
При подробном ознакомлении с теорией управления запасами [1, с. 147-164], можно убедиться, что для уравнений (2) – (4) применим факт оптимальности двухуровневой стратегии управления.
Сформируем правила рационального выбора поставщиков. В первом случае, рассмотрим постоянство фиксированной части затрат на поставку у разных поставщиков (Вариант А). В данном случае каждый поставщик характеризуется парой значений cj, pj. При наличии двух поставщиков с номерами i и j, для которых выполняются оба неравенства вида cj ≥ ci и pj ≥ pi, поставщик под номером j уступает поставщику i по степени надежности и цене.
Обратимся к понятию множества Парето – концепции, введенной в экономической теории, описывающей множество оптимальных решений в многокритериальных задачах оптимизации. Задачах поиска оптимального решения, с учетом нескольких критериев, конфликтующих между собой.
Если в качестве критерия выбран минимум суммарных средних затрат, то среди M поставщиков следует выделить подмножество Парето-оптимальных, отсекая случаи, где может быть найден другой поставщик, для которого при сравнении выполняется неравенство cj ≥ ci и pj ≥ pi при хотя бы одном строгом неравенстве. Итак, в дальнейшем будем считать, что множество поставщиков L является подмножеством Парето, и перестановка двух соседствующих в подмножестве поставщиков, обладающих обратным порядком цен, приводит к снижению средней цены заказа. Естественно, верно обратное: если двух соседствующих в подмножестве поставщиков установлен прямой порядок цен, при их перестановке средняя цена увеличится.
Таким образом, можно заявить, что на каждом шаге при выборе поставщика, оптимальная последовательность обращений к поставщикам сопоставима с их очередностью в подмножестве Парето. (Также, примем что среди поставщиков имеется, как минимум, один абсолютно надежный, логично предположить, что с наиболее высокой стоимостью заказа.)
При оптимальном способе нумерации поставщиков средняя цена поставляемого товара составит величину (5):
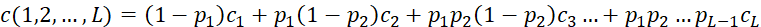 (5)
(5)
Во втором случае, рассмотрим изменчивость фиксированной части затрат на поставку у разных поставщиков (Вариант Б). Как и в первом варианте, последовательность выбора поставщика обусловлена фактором наименьшей стоимости заказа. Однако, логика, описанная для варианта А более неприменима. Решением можно положить исключение поставщиков с тремя параметрами Ai, ci, pi, для которых идет поиск такого поставщика под номером j, для которого будет соблюдено равенство Aj £ Ai, cj £ ci и pj £ pi. Выполнив исключение, можем прибегнуть к использованию результатов предыдущего случая, который в этом случае будет использоваться как следующее эвристическое правило:
Последовательность обращения к поставщикам обусловлена их упорядочиванием по возрастанию стоимости размером u. Последовательность обращений зависит от размера заказа u.
В итоге каждое упорядочивание поставщиков (i1(u), i2(u), …, iL(u)) выстроено по возрастанию величины Aj1(u) + cju. При этом одношаговые затраты 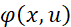 определяются с помощью формулы (6), являющейся комбинацией формул (2) и (7):
определяются с помощью формулы (6), являющейся комбинацией формул (2) и (7):
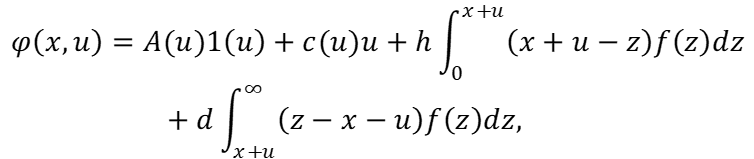 (6)
(6)
Где:
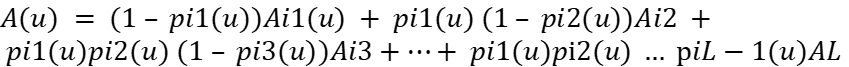 (7)
(7)
и
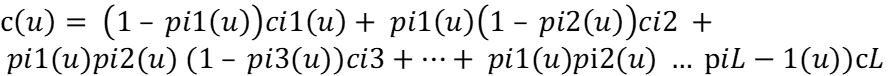 (8)
(8)
Функции 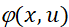 из формул (5) – (7) необходимо подставить в позволяющий рассчитать оптимальные размеры заказов алгоритм (3) – (4).
из формул (5) – (7) необходимо подставить в позволяющий рассчитать оптимальные размеры заказов алгоритм (3) – (4).
Далее, на основе разработанной модели проведем компьютерное моделирование средствами MATLAB. В рамках эксперимента установим ряд зависимостей, и на основе полученной информации примем решения о выборе более выгодной стратегии.
Для моделирования выбираются 4 поставщика, каждый характеризуется следующими параметрами: c цены единицы товара и p вероятностью полного срыва поставки. Рассматриваемые случаи – оптимальный порядок выбора поставщиков ((0,5; 0,8), (1; 0,5), (2; 0,1), (4; 0)) и обратный оптимальному. Средняя цена единицы товара по формуле (5) будет равна 1,38 (оптимальный порядок) и 4 (обратный оптимальному. Это означает закупку товара у самого надёжного поставщика по самой высокой цене.) Для моделирования использованы следующие функции распределения спроса: (a) – экспоненциальное распределение с параметром 𝜆= 0,2; (б) – нормальное распределение с математическим ожиданием 𝜇 = 5 и среднеквадратическим отклонением 𝛿 = 1; (в) – равномерное распределение на отрезке от a = 0 до b = 10.
Рассмотрим зависимости параметров R(A), r(A) оптимальной стратегии управления запасами от стоимости единичной поставки A. Входные данные следующие: стоимость единичной поставки A = 0 ÷ 100; стоимость хранения единицы товара h = 1; удельные потери вследствие дефицита товаров d = 40.
Графики R(A) и r(A) для экспоненциального, Гауссова, равномерного распределения спроса при оптимальном и обратном оптимальном порядке выбора поставщиков, изображены на рисунках соответственно (рис. 1–3).
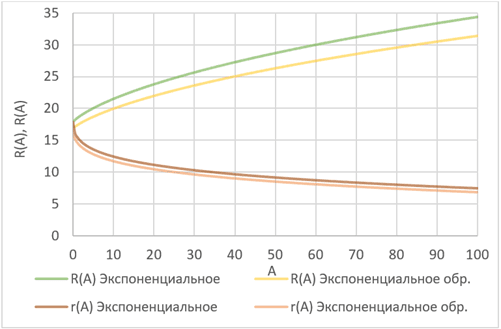
Рис. 1. Графики R(A) и r(A) для экспоненциального распределения спроса
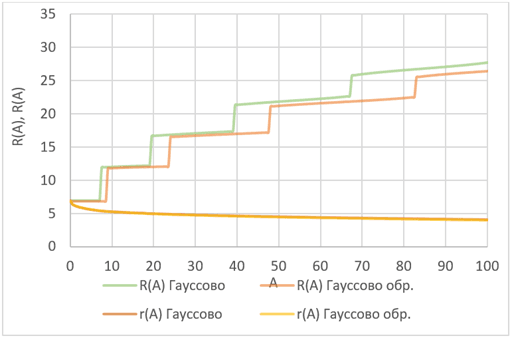
Рис. 2. Графики R(A) и r(A) для Гауссова распределения
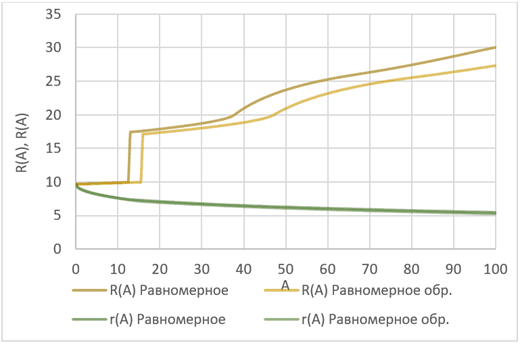
Рис. 3. Графики R(A) и r(A) для равномерного распределения
По информации, полученной из рисунков 1–3, можем сделать вывод, что при росте стоимости отдельной поставки A, значение r(A) уменьшается. Иными словами, тот уровень запасов, при котором сохраняется целесообразность подачи нового заказа, сужается (в ряде случаев, при больших значениях A, уровень может принять отрицательное значение, подразумевая небольшой дефицит внутри системы).
Значения R(A) равномерно растут по мере увеличения значений А. Это свидетельствует, что выгоднее делать заказы большего размера, т. к. стоимость единичной поставки постепенно превосходит расходы на хранение товара. В отличие от порядка выбора поставщиков обратного оптимальному, оптимальный характеризуется большим размером заказа, ведь с увеличением цены при обратном порядке выбора поставщиков, становится экономически выгоднее делать заказы меньшего размера.

.png&w=640&q=75)