Стратегии обработки сигналов пьезодатчиков в электронном барабане

Введение

Прогресс в освоении музыкального инструмента зависит от регулярной практики. На тренировки должно быть выделено большое количество времени. У многих начинающих барабанщиков возникают проблемы с возможностью тренироваться дома, т. к. акустические барабанные установки занимают много места, издают громкие звуки и хорошо передают низкочастотные вибрации через пол и стены, что может приводить к жалобам соседей и невозможности практиковаться у себя в квартире.

Во второй половине прошлого столетия были разработаны первые электронные музыкальные инструменты. Перкуссионные инструменты не стали исключением и сейчас в магазинах можно найти большое количество электронных ударных инструментов, однако большой проблемой является финансовая доступность таких установок. Большинство электронных ударных имеет высокую цену. В сложившейся ситуации сложно найти подходящий и доступный продукт, позволяющий эффективно освоить инструмент.

Значительную часть стоимости электронных барабанных установок составляют проприетарные алгоритмы обработки сигналов. В данной работе рассматриваются стратегии получения сигнала с электронного барабана и предлагаются алгоритмы его обработки, что в дальнейшем может поспособствовать созданию более доступных инструментов.

Обработка сигналов с барабана

Процесс воспроизведения звука удара можно разделить на два этапа:

• Получение сигнала с датчиков.
• Обработка сигнала для определения воспроизводимого звука (определение силы удара (громкость), точки и вида удара (высота и полнота звука), синтез аудиосигнала).

Позиционное считывание

Звук реального барабана зависит от места и силы удара (при ударе ближе к центру звук получается более полным и громким, при ударе ближе к ободу барабана – более плоский и тихий) [4].

Радиальная симметрия барабана позволяет получить только расстояние от центра (вместо точного местоположения) и силу удара для определения звука.

Существует несколько разновидностей пэдов с функцией позиционного считывания. Например, барабаны на несколько зон, работающие с несколькими изолированными друг от друга датчиками. При ударе в строго ограниченную зону головы барабана воспроизводится соответствующий звук.

Наиболее интересный вариант электронных барабанов с позиционным считыванием представляет собой устройство, спроектированное с целью как можно точнее имитировать настоящий акустический барабан.

Этот вариант электронных барабанов использует систему датчиков, сигналы которых позволяют точно определить место и силу удара для синтеза реалистичного звука.

Описание конфигурации датчиков

Для разработки модели выберем конфигурацию барабана и датчиков. Стандартный размер малого барабана – 14 дюймов. Часто можно встретить барабаны 10", 12" или 13", что в некоторых сочетаниях с глубиной, например в 6,5” или 3,5” придает звучанию барабана большую четкость. Выбранный размер барабана – 13 дюймов [1].

Для конфигурации датчиков (рис. 1) был выбран равносторонний треугольник с радиусом описанной окружности 120мм. Такое расположение позволяет воспользоваться радиальной симметрией барабана.

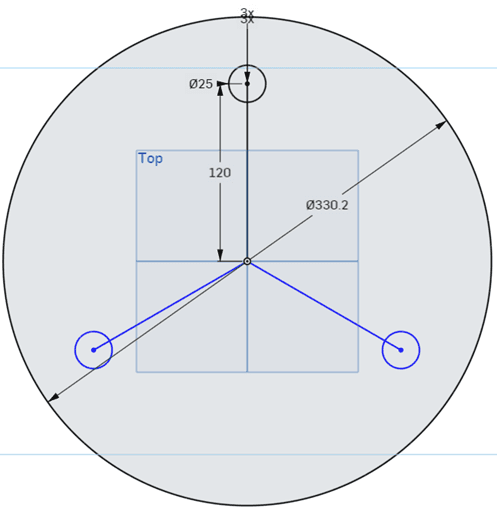
Рис. 1. Конфигурация датчиков

Модель сигнала пьезодатчика

Модель сигнала (рис. 2) пьезодатчика может быть описана следующим уравнением:

Где 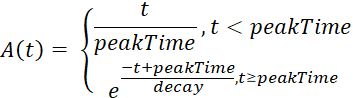 – огибающая сигнала,

– резонансная частота барабана

Резонансная частота (частота настройки) малого барабана, как правило, лежит в диапазоне от 100 до 400 Гц.

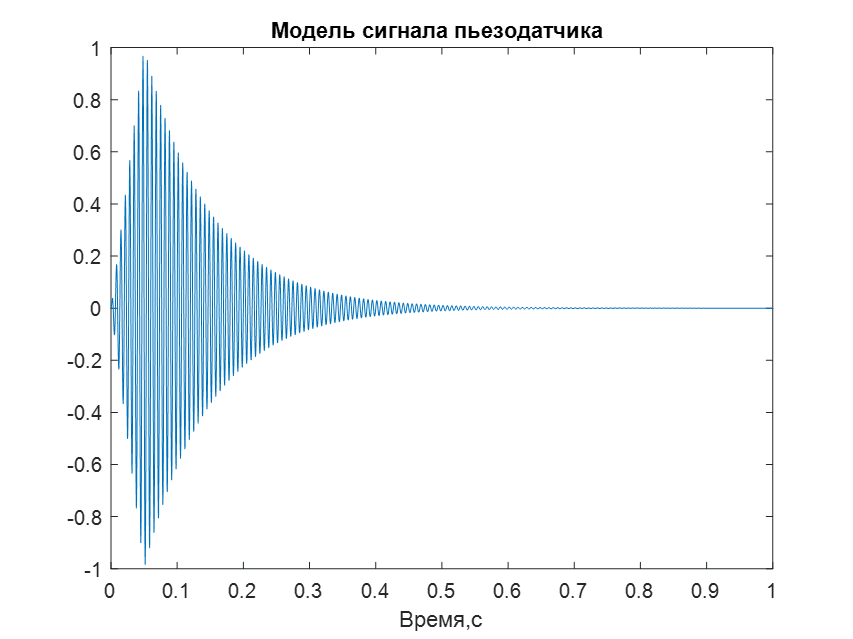
Рис. 2. Модель сигнала пьезодатчика

Зашумим сигнал (рис. 3) для повышения точности модели.

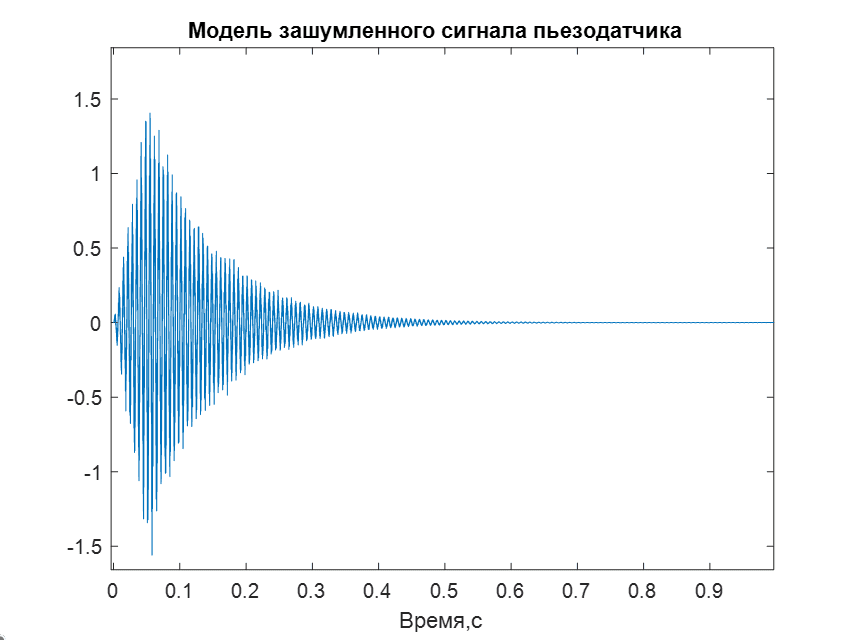
Рис. 3. Модель сигнала пьезодатчика с АБГШ

Чтобы получить значения для цифровой обработки требуется найти максимальные значения сигналов с датчиков и нормировать их. Для этого введем понятия времени сканирования и времени маскирования. Время сканирования – длительность процесса считывания значений сигнала с датчика. Время маскирования – временной промежуток после окончания сканирования, в котором не будет проводиться новое сканирование. Значением для обработки будет максимальное значение сигнала в интервале [t_скан t_маск] (рис. 4).

После получения максимальных значений сигналов с датчиков необходимо выполнить нормирование, чтобы их сумма была равна единице. Для этого требуется разделить каждое значение на сумму трех:

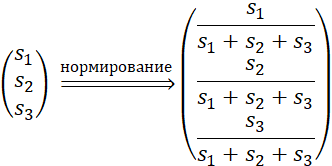
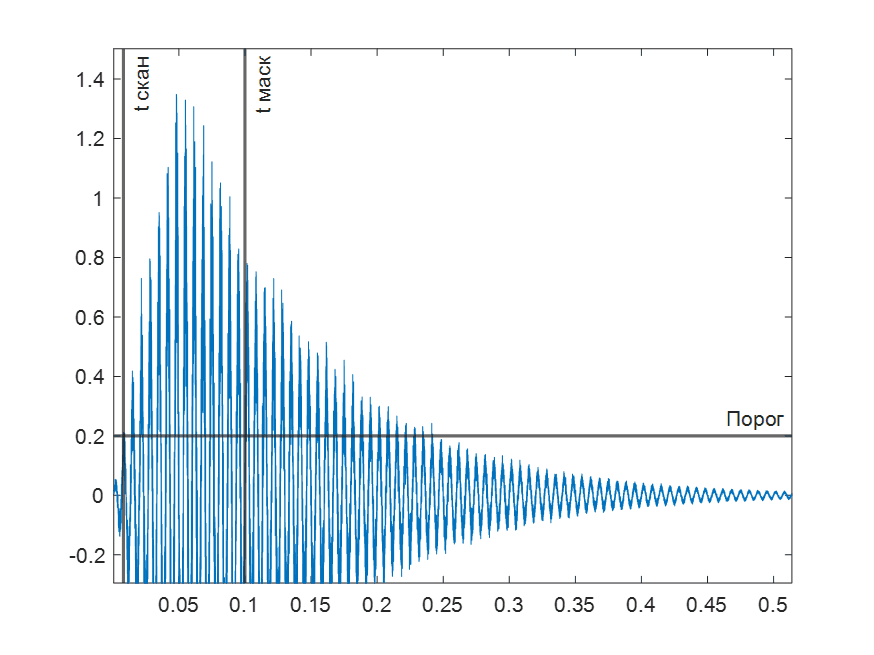
Рис. 4. Предобработка сигнала

Точное решение (Пересечение окружностей)

Если предположить, что максимальное значения отклика датчика обратно пропорционально расстоянию от места удара, то для описания значения отклика можно воспользоваться уравнениями окружностей с известными центрами (координатами датчиков).

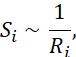
Где Si – максимальное значение отклика i-ого датчика,

R_i – расстояние от точки удара до i-ого датчика.

Точка удара может быть найдена решением системы уравнений:

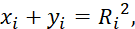
Где x_i,y_i – координаты датчика.

Такой подход будет очень чувствителен к шумам и помехам, т. к. в этом случае решения системы (единственной точки пересечения трех окружностей) может не быть.

Барицентрические координаты

Барицентрическая система координат (БСК) – система координат, в которой положение точки задано по отношению к симплексу (треугольник на плоскости, тетраэдр в пространстве и т. д.). Значения барицентрических координат точки могут быть представлены массами, помещенными в вершины симплекса так, что точка будет являться их центром масс (или барицентром) [2].

Преобразование координат между БСК и ДСК можно описать следующими уравнениями:

БСК в ДСК:

,

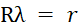Где ,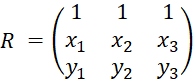

,

,

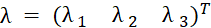ДСК в БСК:

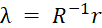
БК точки, лежащей вне симплекса, могут принимать отрицательные значения. Получение верных координат из сигнала с датчиков в данном случае невозможно (сигнала не может быть отрицательным). Для решения этой проблемы необходимо воспользоваться свойством БСК и провести калибровку системы перед использованием.

Сумма координат точки в БСК равна единице. Следовательно, при известных двух координатах возможно вычислить оставшуюся. Для калибровки, помимо нормирования диапазона сигналов датчиков, необходимо найти пороговое значение учета сигнала датчика, ниже которого сигнал будет считаться нулевым. При обнаружении нулевого сигнала с датчика система будет автоматически рассчитывать его значение из свойства БСК, позволяя получить отрицательные значения. При этом, выбранная конфигурация датчиков не позволяет получить значения сигналов ниже порога более чем для одного датчика за удар.

Моделирование нейросетевого алгоритма

Координаты точки удара представляют собой зависимость от сигналов с датчиков. Для аппроксимации таких зависимостей возможно применение нейросетевых алгоритмов. Для задач аппроксимации функций нередко используют сети обобщенной регрессии (GRNN) [3, с. 23-27].

Датасет для обучения и тестирования сети был сгенерирован с помощью метода, представленного в прошлом пункте. Моделирование проводилось в математическом пакете MATLAB. Результат представлен на рисунке 5.

Цвета точек на графика зависят от их номера в последовательности, т. е. точку из входного сигнала возможно распознать по ее цвету в выходном сигнале. На графиках моделирования можно увидеть похожую структуру входного и выходного сигналов.

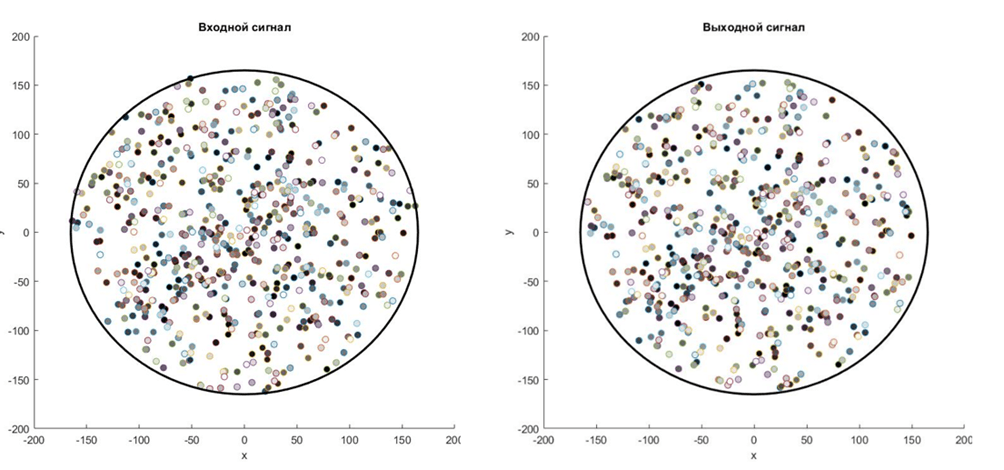
Рис. 5. Результаты моделирования нейросетевого алгоритма

Цвета точек на графиках зависят от их номера в последовательности, т. е. точку из входного сигнала возможно распознать по ее цвету в выходном сигнале. На графиках моделирования можно увидеть похожую структуру входного и выходного сигналов.

Для численной оценки модели были рассчитаны метрики MSE, MAE и найдена наибольшая ошибка.

MSE = 4.95

MAE = 1.37

maxError = 16.67

Ошибка сети представляет собой вектор разницы между входной точкой и выходной. Значения метрик показывают, что модель выдает точку со средней ошибкой 1.37 мм, максимальная ошибка составила 16.67 мм.

При стандартном диаметре барабанной палочки 1.45 см, вероятнее всего, что подобные ошибки не будут заметны при игре. Следовательно, можно говорить о работоспособности модели.