Методы решения задач многокритериальной оптимизации с линейными функциями цели

Введение

Под понятием оптимизации понимают выбор наилучшего варианта из множества всех доступных вариантов на основе определенных критериев. Проблемы оптимизации существуют во всех количественных дисциплинах, от информатики и инженерии до исследования операций и экономики.

Задача оптимизации состоит из минимизации или максимизации целевой функции, определенной в области конечномерного векторного пространства и определяемой набором линейных, нелинейных и/или неравенств [2]. Целевая функция показывает зависимость критерия оптимальности от параметров, влияющих на ее значение.

Многокритериальная оптимизация представляет собой область принятия, с учетом множества критериев. Она относится к сфере решения оптимизационных задач, в которых необходимо одновременно оптимизировать две или более целевые функции. Во многих научных областях прибегают к использованию инструментов многокритериальной оптимизации. Например, в технике, экономике и логистике, этот происходит, когда преследуются две и более противоречащие друг другу цели, однако должно быть принято такое оптимальное решение, которое будет удовлетворять этим целям [6].

1. Постановка задачи многокритериальной оптимизации

Рассмотрим задачу многокритериальной оптимизации и представим ее в математическом виде.

Задача многокритериальной оптимизации задается четырьмя составными элементами: набором переменных, целевыми функциями, допустимым множеством и дополнительными ограничениями. На практике может решаться как задача максимизации, так и минимизации. Поэтому для нахождения, соответствующего ограничениям, оптимального набора решений, потребуется указать критерии поиска.

В ходе решения данной задачи будет выполняться поиск вектора переменных, который будет удовлетворять всем заданным ограничениям. Далее, будет проводиться оптимизация векторной функцией, целевые функции являются ее элементами [5].

В общем виде для задач многокритериальной оптимизации не получается найти единственное решение, что является особенностью задач такого типа [4].

В общем виде для задач многокритериальной оптимизации не получается найти единственное решение, что является особенностью задач такого типа [4].

При решении задачи многокритериальной оптимизации положим, что целевые функции заданы в евклидовом пространстве Rⁿ – n-мерное векторное пространство.

Через  обозначим вектор переменных модели, пусть Обозначим i-й частный критерий оптимальности через . Обозначим через S множество допустимых значений переменных модели. Тогда для каждого вектора , принадлежащего множеству S, определено значение i-го частного критерия оптимальности

Таким образом, если учитывать, что задачу минимизации всегда можно свести к задаче максимизации, с помощью изменения знака функции:

где S – непустая область определения.

целевых функций;

– вектор решений;

– вектор ограничений. 

2. Некоторые методы решения многокритериальных оптимизационных задач 

Задачи многокритериальной оптимизации решаются различными методами, в данной работе будут рассмотрены следующие из них:

1. Метод свертки;
2. Метод последовательных уступок на основе метрики в пространстве критериев;
3. Метод идеальной точки.

Начнем с рассмотрения метода свертки. Метод свертки предполагает преобразование многокритериальной задачи в однокритериальную путем сбора общего критерия из всех исходных критериев. Каждому критерию присваивается весовой коэффициент, отражающий относительную важность соответствующего критерия. Существует множество различных типов сверток: аддитивные, мультипликативные и т. д.

Методы свертки критериев широко используются для решения задач многокритериальной оптимизации, но это не отменяет факта наличия у них ряда недостатков. Недостатки методов свертывания критериев могут помешать обосновать выбор метода свертки. Вместе с тем, иногда бывает крайне сложно привести аргументы в поддержку выбора весовых коэффициентов. В таких случаях приходится прибегать к привлечению дополнительных ресурсов. Совокупность всех этих факторов приводит к существенным затратам. Кроме всего прочего, снижение качества по одному критерию не всегда может быть компенсировано улучшением качества по другому критерию [5].

В данной работе речь пойдет об аддитивном методе свертки. В таком типе свертки глобальным критерием является взвешенная сумма критериев, указанных в задаче. Сумма весовых коэффициентов должна быть равна 1, а все коэффициенты должны быть неотрицательны [3].

Алгоритм метода аддитивной свертки:

1. Определение весовых коэффициентов, сумма весовых коэффициентов равна единице, все коэффициенты неотрицательны;
2. Построение функции взвешенной аддитивной свертки и ее исследование.

Функция взвешенной аддитивной свертки выглядит следующим образом:

,

где  – весовой коэффициент каждого критерия.

После проведения свертки, решается однокритериальная задача оптимизации с использованием симплексного метода.

Поскольку определить сравнительную значимость между критериями сложно, положим, что изучаемые в данной работе критерии равнозначны и их весовые коэффициенты имеют одинаковые значения.

Далее приступим к разбору метода последовательных уступок. При использовании этого метода все критерии сортируются в порядке убывания их приоритета, т.е. степени важности. Задачи оптимизации по каждому критерию решаются последовательно, причем каждый новый шаг ограничивает предыдущий более значимый критерий.

Перечислим этапы метода последовательных уступок, учитывая, что критерии перечислены в порядке убывания приоритета.

Алгоритм данного метода:

1 этап. Решение задачи относительно первого критерия 

Вычисление первой уступки 

2 этап. Решение задачи относительно второго критерия

При условии добавления к исходным ограничениям нового, накладываемого относительно уступки

где - оптимальное решение для 1-го критерия.

Вычисление второй уступки

n этап. Решение задачи относительно i-го критерия

При условии добавления нового ограничения, накладываемых относительно уступок к заданным ограничениям

Решение, полученное на последнем этапе, является оптимальным.

Теперь переходим к методу идеальной точки. Метод заключается в нахождении точки, наиболее близкой к идеальной [1]. Идеальная точка – это то, что считается лучшим из возможных решений. Координаты идеальной точки представляют собой комбинацию лучших значений заданных параметров. Может возникнуть случай, когда, с учетом всех ограничений, идеальная точка не будет входить в рассматриваемое в задаче множество. Тогда она будет считаться нереализуемой, и в этом случае ее называют точкой утопии. В процессе реализации данного метода с идеальной точкой сравнивают объекты, принадлежащие множеству критериев. После этого, находят расстояние от каждого такого объекта до идеальной точки [7].

,

где a_i – минимально возможное значение по критерию i

Точка a является идеальной, т.е. оптимальной по всем критериям.

Вычисляется Евклидово расстояние между каждым критерием и идеальной точкой:

Задача принимает следующий вид:

Пройдемся по шагам алгоритма идеальной точки:

1. Формирование «идеальной точки» т.е. поиск оптимального решение относительно каждого критерия;
2. Определение для каждого критерия многокритериальной метрики (расстояния) до «идеальной точки».

Найденная идеальная точка:

где  – это оптимальное решение однокритериальной задачи для i-го критерия.

Полученная вспомогательная задача:

Если после применения метода идеальной точки задача была успешно сведена к однокритериальной оптимизационной задаче с выпуклой гладкой целевой функцией и линейными ограничениями, то ее можно решить с помощью метода условного градиента.

3. Экспериментальная часть

Чтобы отразить практическую пользу разработанного для данной работы программного продукта и численно сравнить результаты ее решения рассматриваемыми методами многокритериальной оптимизации. Подобные задачи встречаются в процессе деятельности реальных организаций.

Перейдем к условиям задачи. Молокоперерабатывающий комбинат принял решение о начале выпуска нового вида продукции. Для этого требуется разработать план выпуска такого продукта. Основные затраты на разработку составляют затраты на модернизацию оборудования  и затраты на научные исследования  При этом себестоимость единицы продукции находится в зависимости от затрат , а качество продукции . Перед ЛПР (лицом принимающим решение) встает задача минимизации себестоимости (цены) вводимого продукта и максимизации качества выпускаемой продукции. Требуется решить задачу и найти оптимальные значения факторов , а также значения целевых функций, с учетом ограничений, наложенных на факторы, вида:

Задача минимизации первого критерия заменяется на задачу максимизации:

Для проведения экспериментальной части было разработано приложение, которое обеспечивает решение задачи многокритериальной оптимизации. В созданной программе пользователю предоставляется выбора одного из двух методов решения: метода свертки или метода с использованием метрики в пространстве критериев (идеальной точки).

Приведем решение описанной выше прикладной задачи многокритериальной оптимизации с привлечением исследуемых методов посредством применения программы, реализующей их.

Сначала поставленная ранее задача решается методом свертки, как показано на рис. 1.

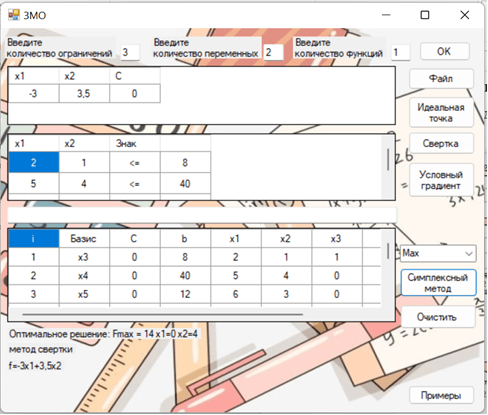
Рис. 1. Решение производственной задачи методом свертки

Задача решена, оптимальное решение найдено. Теперь решим поставленную задачу методом идеальной точки, как показано на рис. 2.

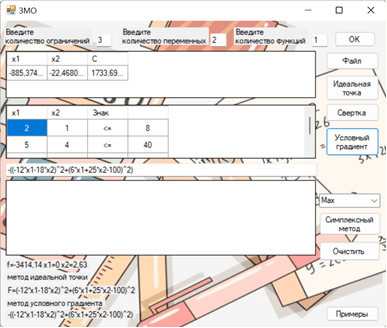
Рис. 2. Решение производственной задачи методом идеальной точки

Оптимальное решение найдено, задача решена. Сравним результаты двух методов. Оптимальное решение по методу свертки критериев:

Оптимальное решение по методу «идеальной точки»:

Применяя данные методы, были получены результаты, которые отличны друг от друга.

Далее в ходе исследования, с использованием разработанного программного продукта, проводилось эксперименты с применением рассматриваемых методов на нескольких тестовых примерах различной размерности, а также численное сравнение исследуемых методов между собой.

Получаемые при решении методом свертки задач различной размерности ответы отличаются от результатов, которые были получены при решении тех же задач методом с использованием метрики в пространстве критериев (идеальной точки). Такое явление может быть следствием того, что задачи многокритериальной оптимизации не имеют общего решения, только частные случаи, которые зависят от многих факторов, имеют оптимальные решения.

Заключение

Настоящая работа была выполнена в соответствии с поставленными целью. В ходе ее выполнения была разработана программа, с помощью которой можно несколькими методами решать задачи многокритериальной оптимизации.

В рамках исследования были выявлены подробные характеристики двух заданных методов и проведен их сравнительный анализ. Решена задача, которая раскрывает преимуществ и недостатков этих методов. Реализованный программный продукт может использоваться не только в учебных целях, но и в ходе практической деятельности при работе в различных организациях, что подтверждается результатами экспериментов.