Подгонки под результат в квантовой механике и физике. Парадокс наличия в атоме нулевой энергии. Часть 2

В [1, с. 12-32] мы подробно показали, какие подгонки под результат были допущены при определении первой боровской орбиты по теории Бора и при вычислении спектра водородоподобного атома. Главной ошибкой Бора был отказ от излучения электронов при движении на дискретных орбитах вокруг протона, что противоречило законам электродинамики. Соответственно мы выявили причину совпадения практических результатов с данными подгонками под результат.

Как уже отмечалось в [1, с. 12-32] данные подгонки являются результатом отсутствия понимания логики возникновения физических законов от простого состояния к сложному состоянию. Физический закон воспринимался в качестве постулата, и не рассматривалась причина его появления. Отсюда, чтобы получить совпадение теории с практикой стали использоваться способы «сшивания решений» с наличием неких постулатов. В классической электродинамике такой метод «сшивания решений» относится к рассмотрению процессов на границе раздела сред. Какие парадоксы при этом возникают и как они решаются мы описали в [2, с. 6-17]. Недостаток метода «сшивания решений» в том, что результат зависит от того, какие начальные условия (иной раз необоснованные) принимаются за основу, что и даёт подгонку под результат. Однако есть противоречия, которые невозможно решить на основе даже таких подгоночных подходов. Например, искривление прохождения света в так называемом гравитационном поле (результат представления пространства и времени в ОТО Эйнштейна) нельзя описать на основе принципа замедления движения света, так как это противоречит СТО Эйнштейна. Действительно, если бы свет имел замедление в так называемом гравитационном поле (среде распространения), то он повторял бы свойства частиц. Для корпускулярных частиц суть замедления связана с торможением. Однако свет при выходе из более плотной оптической среды продолжает движение со скоростью света. Это говорит о том, что замедление скорости света связано не с торможением, а с взаимодействием с элементами оптически плотной среды через поглощение и излучение, что и интерпретируется как торможение. Результатом подтверждения этого является принцип Гюйгенса-Френеля с наличием вторичных источников возбуждения в так называемом вакууме. Более того, интерференция света с учётом принципа суперпозиции приводила бы к исчезновению электромагнитного поля при сложении в противофазе, и дальнейшее распространение света было бы невозможно. Но этого не наблюдается, что также говорит о наличии взаимодействия света со средой с поглощением и излучением, отсюда и требование к наличию вторичных (сторонних или фиктивных) источников излучения. То есть так называемое гравитационное поле представляет собой корпускулярно-волновой объект, который характеризуется корпускулярными свойствами через значения электрической (ε₀) и магнитной проницаемости (μ₀), а волновые свойства определяются вторичными источниками поглощения и излучения. Взаимодействие через излучение и поглощение приводит к изменению направления движения света, а исчезновение электромагнитного поля и появление его вновь связано с преобразованием кинетической энергии в потенциальную энергию, и, наоборот (без преобразования нет и причин для изменений). Это говорит о том, что при решении задач необходимо учитывать принципы физического взаимодействия любого объекта со средой, что и было показано нами в [1] с исключением парадоксов. Однако, в квантовой механике к методу «сшивания решений» добавился и вероятностный подход, связанный с тем, что Нильс Бор не смог решить задачу восполнения энергии, излучаемой электроном, который вращается вокруг протона. Поэтому, чтобы обосновать запрет излучения придумали движение электрона не по орбите, а в виде орбиталей, получаемых вероятностным образом в виде волновых функций (рис. 1).

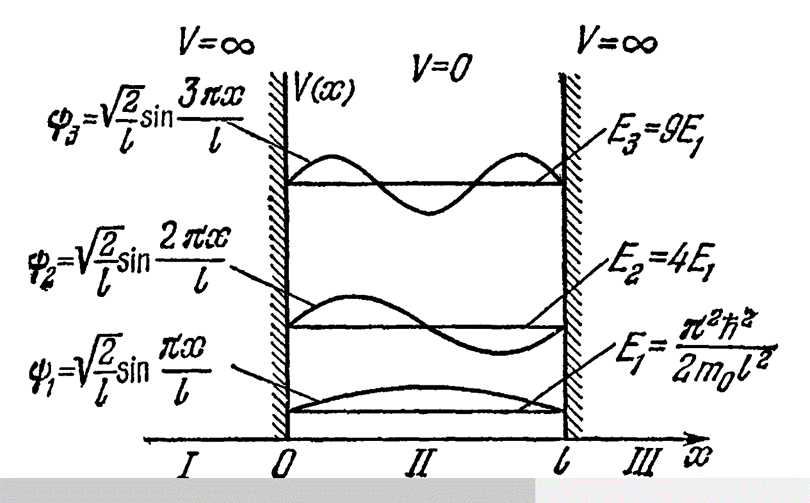
Рис. 1. Частица в потенциальной яме с бесконечно высокими стенками

Соответственно приводим ссылку из [3, с. 114]: «Хотя представление об орбитах, как и вообще представление о траекториях микрочастиц, является неправомерным, момент, обусловленный движением электронов в атоме, называют орбитальным». Читатель, с нормальным логическим мышлением, сразу обратит внимание на парадокс, при котором волновой вид определяется закономерностью детерминированного физического закона, а он явно противоречит вероятности, которая исключает любую закономерность, а значит и физический закон. Действительно, вероятность ввели для того, чтобы убрать физический закон, связанный с излучением при детерминированном движении электрона по орбите вокруг протона, но представили при этом волновую функцию в качестве основы для вероятности, что говорит уже о наличии физического закона. Тогда любое волновое движение не может обойтись без изменения направления с наличием ускорений и замедлений в соответствии с наличием волнового вида (отсутствие детерминированной закономерности – это «белый шум»), а это опять должно давать излучение. Иными словами, от чего ушли, к тому и пришли, но на основе вероятности при «сшивании решений» придумали телепортацию через потенциальный барьер и назвали его туннельным эффектом [4, с. 89] (рис. 2).

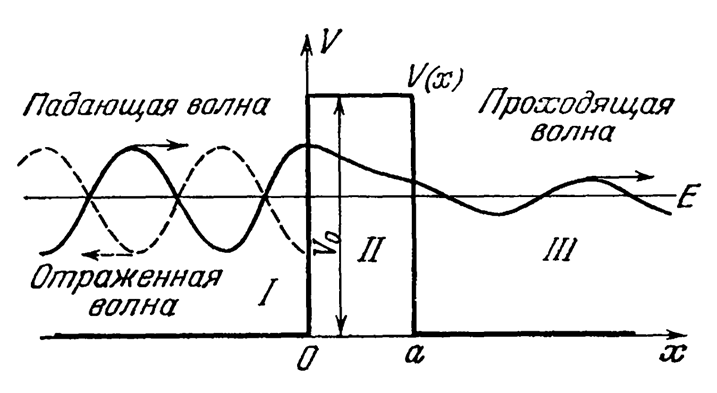
Рис. 2. Прохождение частицы сквозь потенциальный барьер прямоугольной формы

А это означает, что опровергли разом необходимость СТО Эйнштейна и необходимость наличия любых физических законов. При этом значение волновой функции должно иметь на границе раздела сред максимальное значение, что противоречит минимуму функции по рисунку 1, из которого также видно, что для волновых функций со значением с величиной Е₁ и Е₃ наибольшая вероятность будет в том самом месте, где должен находиться протон. Собственно наличие таких чудес «узаконили» на основании соотношения неопределённостей Гейзенберга [5, с. 69]. Далее обман с подгонкой под результат в физике и квантовой механике идёт по возрастающему процессу, так как отсутствие закономерностей означает наличие любых чудес.

Поэтому нам необходимо раскрыть каким образом получались результаты, совпадающие с практикой, и с чем это связано. Понятно, что основу взаимодействия объектов, таких как электрон и протон, составляют электрические и магнитные силы. Отсюда необходимо обратить внимание на их взаимодействие. Вначале электрон рассматривали как частицу с отрицательным зарядом, а наличие магнитного момента связывали с движением электрона вокруг протона. Действительно, в элементарной боровской теории водородного атома магнитные силы отсутствуют [6, с. 59]. По сути, они заменены на центробежные силы. В этом случае уравнение движения электрона имеет вид [6, с. 59]:

(1)

При этом наличие магнитного орбитального момента связывали с движением по формуле [7, с. 159]:

(2)

Иными словами, магнитный момент образуется на основе кругового замкнутого движения. Одновременно движущийся по орбите электрон обладает орбитальным механическим моментом [7, с. 159]:

(3)

Соответственно, отношение магнитного момента элементарной частицы к её механическому моменту называется магнитомеханическим (или гиромагнитным) отношением:

(4)

Здесь учитывается что, так как по дираковской теории «дырок» значение заряда имеет значение ±1 [8, с. 350] (в противном случае в формуле энергии Эйнштейна существовал бы член с зарядом, так как воздействия без энергии не бывает), то отличие связано только с массой покоя электрона, которая для соблюдения СТО и ОТО Эйнштейна в противоположности равняется скорости света, то есть m₀=1/c=h. Это было подробно показано нами в [9, с. 3-23] на основании вывода уравнения энергии Эйнштейна из уравнения окружности, которое в свою очередь соответствует преобразованиям Лоренца-Миковского, то есть СТО Эйнштейна.

Понятно, что мы подразумеваем, что в Мироздании ch=1. Нечто подобное равенству сh=1 было введено также в квантовую механику [10, с. 341] и получило название постоянной тонкой структуры (отличие только в нормировке и в принятой системе величин СИ):

(5)

С учётом теории Дирака при заряде [8, с. 350] получаем . Иными словами, механический момент и магнитный момент однозначно связаны через скорость света (или постоянную Планка). Собственно, иное противоречило бы наличию связи противоположностей, и тогда электромагнитная волна никак бы не зависела от пространственно-временного искривления по СТО и ОТО Эйнштейна. Именно это не понимают современные физики, так как нет независимых компонент в силу наличия законов сохранения количества при преобразованиях.

Однако магнитная составляющая также однозначно связана с электрической составляющей, что определено усовершенствованными уравнениями Максвелла [11, с. 10-24]. В противном случае мы имели бы независимость электрических сил от магнитных сил или неоднозначность образования, что также противоречит наличию законов физики. Поэтому и существует однозначная связь силы Лоренца и силы Кулона в соответствии с СТО и ОТО Эйнштейна, что также было выведено до нас. Отсюда любое движение связано с образованием не только магнитных, но и электрических сил. Практически зависимость от движения также было получено до нас, когда Дирак, исходя из уравнения энергии Эйнштейна, вывел свою систему уравнений [12, с. 295], где движение выражено через волновые функции, дающие вероятность. Нам оставалось лишь заменить, вероятностные волновые функции на реальные электромагнитные функции на основе усовершенствованных уравнений Максвелла [11, с. 10-24], что и дало связь механического импульса движения с электромагнитными составляющими.

Соответственно энергия движения должна делиться между этими составляющими, и такое деление энергии движения, пересчитанное в тепловое движение в виде kT, было предложено в формуле Рэлея-Джинса [13, с. 25]. Это определяет наличие коэффициента равного двойке в формуле (4) и фактически также было введено в квантовую механику до нас. Физикам оставалось лишь сделать правильные выводы из того, что уже было подтверждено на практике, но так как они не исходили из наличия необходимости существования противоположностей в каждом объекте Мироздания, то они пошли по пути чудес.

Снова отметим, что любой объект Мироздания имеет замкнутую и разомкнутую составляющую (это и есть корпускулярно-волновой дуализм любого объекта). В противном случае он просто не может существовать, так как тогда были бы возможны полностью замкнутые объекты (это ноль) или разомкнутые объекты (это отсутствие отличий в виде однородности). Если бы движение давало бы только замкнутую магнитную составляющую, то это уже изначально давало бы парадокс отсутствия взаимодействия. И вот тут требуется наличие противоположностей, когда замкнутый процесс в одной противоположности представляется разомкнутым в другой противоположности для взаимодействия. Далее в квантовой механике делается замена центробежной силы с учётом механического момента по формуле [6, с. 59]:

(6)

Как мы показали в [1, с. 12-32], данный вывод может быть получен на основании формулы Луи де Бройля, которая также выводится из аргумента волновой функции с учётом связи длины и времени через скорость света, что, собственно, ввёл Минковский [14, с. 226] в виде:

(7)

И если считать, что имеем круговое движение в аргументе функции (а это тоже не наша выдумка и используется при определении магнитного момента при сверхпроводимости [15, с. 492] и соответствует тому, что замкнутое движение в одной противоположности – это прямолинейное движение в другой противоположности), то получим соответствие c (6) в виде:

(8)

Другими словами, для формулы Луи де Бройля при описании соответствия механического момента импульса величине кратной осуществлён переход от прямолинейного движения со скоростью v к замкнутому движению с выполнением того же самого закона. Собственно, это связано с тем, что длина волны Луи де Бройля отражает по нашей теории излучение и поглощение электромагнитных волн в равном количестве. Отсюда мы имеем . Само это излучение (поглощение) формируется за счёт вращения объекта с радиусом r в противоположности из-за наличия изменения направления по окружности, то есть энергия предыдущего направления излучается, а энергия следующего направления поглощается. Равенство излучения и поглощения определяется отсутствием распада объекта. Отметим, что если бы не было преобразования замкнутого движения в одной противоположности в прямолинейное движение в другой противоположности, то не было бы отличий между противоположностями. Поэтому здесь необходимо учитывать разницу на 2π, то есть меняется и размерность (уровень иерархии при обратно-пропорциональной связи между противоположностями) в силу того, что иное, при условии закона объединения (синтеза) в одной противоположности и эквивалентного распада в другой противоположности не обеспечит наличие закона сохранения энергии между противоположностями. Изменение на 2π ‒ это тоже не наша выдумка и связано с иерархическим построением Мироздания в противоположностях, и мы это покажем несколько ниже. Далее в квантовой механике осуществляется переход в противоположность с заменой центробежных сил на основе импульса на значение кратное постоянной Планка:

(9)

После подстановки, при n=1, получили радиус первой орбиты водородного атома:

(10)

Однако данный результат основан на наличии значений констант в системе измерения СГС без учёта параметров среды. В итоге получатся неоднозначность, так как по теории Дирака при выводе его системы уравнений из уравнения энергии Эйнштейна значение заряда q=e₀=±1. Ещё раз отметим, что под заряд в уравнении Эйнштейна нет энергии для силового воздействия. Отсюда попытка представить в кварках значения зарядов в виде ±1/3 и ±2/3, это чистая фантазия физиков, так как при разных зарядах имеется один и тот же спин равный ½, что исключает однозначную связь электрических и магнитных сил. И если исходить из нашей теории [3, с. 114], с учётом того, что , то получим:

(11)

Другими словами, при использовании системы измерения Мироздания, где есть только количество и закономерности, радиус первой боровской орбиты оказывается меньше, чем постоянная Планка, и это ‒ парадокс, если считать, что в нашей системе наблюдения минимальный размер не может быть менее постоянной Планка h, так как по формуле Луи де Бройля (8) М=r₀p=h. Иными словами, в формулу (9) мы должны подставлять значение радиуса не с учётом длины волны, а значение радиуса, при котором волна в одной противоположности выражает корпускулярные свойства в виде длины в другой противоположности. Это эквивалентно переходу от кинетической энергии в виде волны к потенциальной энергии пространственно-временного искривления. В этом случае с учётом нашей теории [3, с. 114] при m₀=1/c=h получим . Отметим, что в классической электродинамике [16, с. 276] радиус электрона вычисляется по формуле:

(12)

С учётом нашей теории , и эта величина соответствует логике, по которой минимальный дискретный объект должен быть соизмерим с постоянной Планка. Меньше такого изменения ничего быть не может, иначе мы бы имели вариант «ультрафиолетовой катастрофы», связанной с бесконечной энергией. Иными словами, фактически по формуле (9) мы получили, что движение в одной противоположности, выраженное через момент импульса (что характеризует кинетическую волновую энергию), в другой противоположности даёт корпускулярный объект типа электрона с минимальными размерами в виде постоянной Планка (h). Понятно, что меньше корпускулярной частицы в виде электрона (позитрона) ничего быть не может, так как мы бы имели распад на более мелкие частицы, а реально уже электрон и позитрон преобразуются в противоположность через аннигиляцию. В противном случае нет обоснований для перехода от волновых свойств к корпускулярным свойствам, и наоборот, как это наблюдается на практике при аннигиляции электрона и позитрона. Надо отметить, что в равенстве (9) учитывается, что электрические силы выражены через взаимодействие двух противоположных частиц, что при обмене эквивалентно удвоению силы, и поэтому, чтобы получить равенство магнитных и электрических сил в формулу (9) подставляется значение механического момента полностью, а не половина, которая отражает магнитные силы. Таким образом, мы получаем связь электрических и магнитных сил через значение h=1/c, что характеризует их как противоположности. С учетом обратно-пропорциональной связи между противоположностями их произведение должно равняться единице вида ch=1. Таким образом, мы видим, что теория Бора является подгонкой под результат, но соответственно здесь важен вопрос, почему было получено значение постоянной Ридберга. Постоянная Ридберга с учётом постоянной тонкой структуры имеет величину:

(13)

Соответственно учтём, что , отсюда получаем:

(14)

По нашей теории (если учесть, что m₀c=hc=1) постоянная Ридберга будет определяться в виде:

(15)

Иными словами, система измерения в Мироздании, основанная на количестве и закономерностях, не совпадает с системами измерения придуманными людьми (СИ и СГС). Как мы отмечали в [1, с. 12-32], значение связано с системой измерения СГС и фактически именно это значение определяет в этой системе измерения разницу между первой боровской орбитой и радиусом электрона. Значение , как мы отмечали выше, связано с переходом в противоположность от корпускулярных свойств механического движения с вращением к волновым свойствам. Это аналогично переходу от значения ћ к 2πћ. Переход в противоположность обычно выражается в изменении, например, при дифференцировании или интегрировании экспоненциальной функции. Это, собственно, приводит к смене уровня иерархии в Мироздании, так как в противном случае мы имели бы возможность замкнутых процессов на одном уровне с возможностью создания вечного двигателя.

Отсюда, постоянная Ридберга определяет коэффициент, связанный с максимально возможным количеством объектов в Мироздании при переходе из одной противоположности в другую в виде величины N/2=c/(2h) через излучение. Полное значение N получится при учёте излучения и поглощения. Иными словами, в нашей теории постоянная Ридберга имеет логическое и физическое обоснование. При этом, чтобы получить взаимосвязь всех N объектов между собой необходимо соблюсти условие ch=1, иначе будут объекты не участвующие во взаимодействии. Этот же результат для постоянной Ридберга мы получаем в формуле (4). При этом механический момент фактически выступает как аналог потенциальных электрических сил при обратно-пропорциональной связи кинетической энергии с потенциальной через h=1/c.

Кроме того известно, что электрические силы и магнитные силы отражают противоположности, связанные через скорость света (Н=сЕ). В этом случае с учётом того, что в формуле (4) рассматривалось взаимодействие электрических сил от двух противоположных частиц, что дало коэффициент равный двойке, а минимальный объект при создании электрических сил имеет значение Е=h (это минимальное искривление дающее разницу для формирования воздействия силы), получаем Н/(2Е)=p_m /(hM)=c/(2h)=N/2. Иными словами, любое излучение, впрочем, как и поглощение, определяется постоянной Ридберга, как результат начального взаимодействия через обмен наиболее простых объектов Мироздания и далее результат зависит от количества объектов участвующих во взаимодействии.

Однако возникает вопрос: «Каким образом происходит преобразование электромагнитных колебаний в одной противоположности в корпускулярные объекты в другой противоположности и наоборот?»

Данный переход был получен на практике [17, с. 273], где гамма-фотон при соответствующей кинетической энергии сталкивается, например, с электроном, в результате чего образуется дополнительная пара электрона и позитрона. Соответственно аннигиляция электрона и позитрона даёт гамма-фотон. Однако в уравнения Дирака при описании свойств частицы входили в качестве начальных при массе покоя равных нулю не электромагнитные волны, а уравнения для электронных и мюонных нейтрино (антинейтрино), выраженные через волновые функции Луи де Бройля. Поэтому надо было показать, как из взаимодействия электронных и мюонных нейтрино (антинейтрино) получаются электромагнитные волны, дающие гамма-фотоны. Это было нами сделано в [18, с. 40-56], а в [19, с .32-58] показано, как на основе наличия и взаимодействия электронных и мюонных нейтрино (антинейтрино) формируются любые объекты Мироздания. При этом на основе усовершенствованных уравнений Максвелла, которые заменили уравнения Дирака с неизвестными волновыми функциями (дающими вероятность нахождения частицы), был показан метод расчёта движения электрона при воздействии внешних электрических и магнитных сил. Иными словами, мы должны описывать любой объект Мироздания на основе его корпускулярных и волновых свойств. Собственно, вначале по этому пути и пошла наука. В 1924 г. связь волновых свойств с корпускулярными свойствами показал Луи де Бройль через его известную формулу (8) и она была подтверждена экспериментально [20, с. 63] в опытах Дэвиссона и Джермера в 1927 г. Более того, преобразование электромагнитной волны в кинетическую энергию частицы, и наоборот, было показано в 1923 г. при исследовании рассеяния рентгеновских лучей свободными электронами – эффект Комптона, где в результате взаимодействия электромагнитной волны одной частоты с электроном, появлялась электромагнитная волна другой частоты. Здесь помимо закона сохранения энергии соблюдался ещё и закон сохранения импульса [21, с. 15-30]. Если исходить из взаимодействия только по классической электродинамике, то при рассеянии света свободными электронами его частота не изменяется (f_нач=f_кон). Идея электромагнитной теории массы пришла в голову и первооткрывателю электрона Дж. Дж. Томсону, однако он не смог разобраться в механизме взаимодействия противоположностей и на основании классических уравнений Максвелла создать математическую модель оказалось невозможно.

Понятно, что для взаимодействия необходимо было совместить волновые свойства с корпускулярными свойствами в одном уравнении. Поэтому в развитии идеи де Бройля о волновых свойствах вещества Э. Шредингер в 1926 г. получил своё знаменитое уравнение [22, с. 72] в виде:

(16)

Для комплексно-сопряжённого уравнения Шредингера имеем:

(17)

При этом волновая функция Ψ для (16) имела вид:

(18)

При подстановке (18) в (16) получалось известное классическое соотношение между энергией и импульсом частицы при отсутствии внешних сил:

(19)

При Е=hf и p=h/λ получаем формулу Луи де Бройля (8).

Отметим, что при подходе, предложенном Шредингером, рассматривалось начальное корпускулярное уравнение Гамильтона-Якоби [23, с. 29]:

(20)

Однако сама замена значения S (r, t) на экспоненциальную функцию была совершена произвольно, и не позволяла понять, как из волновых свойств получаются корпускулярные свойства. При этом получалось, что если в качестве волновой функции взять электромагнитную волну, то получался парадокс, связанный с тем, что электромагнитная волна имела движение со скоростью света. Поэтому в 1928 г. Дирак посредством «линеаризации» уравнения энергии Эйнштейна предложил свою систему уравнений [24, с. 295], где фактически корпускулярные свойства частицы получались за счёт взаимодействия уравнений Дирака через подстановку одних уравнений в другие. Иными словами, исходя из системы уравнений, фактически Дирак ввёл взаимодействие электронных и мюонных нейтрино (антинейтрино) через подстановку одних уравнений в другие, и это не понимают современные физики и пытаются опровергнуть такое взаимодействие. То есть получался замкнутый вид взаимодействия через излучение и поглощение в равных количествах, что решало проблему совместимости по скорости. При этом волновая функция исключалась из конечного уравнения в силу её присутствия во всех членах уравнения, и рассматривались только корпускулярные свойства.

Так же отметим, что физики не поняли саму суть необходимости излучения и поглощения для взаимодействия, и для них оставался вопрос, который не был решён, и он был связан с тем, что было непонятно, что собой представляют эти самые волновые функции Луи де Бройля. Кроме того, классические уравнения Максвелла (а не усовершенствованные уравнения Максвелла, предложенные нами) не позволяли их совместить с уравнениями Дирака. Помимо этого, Шрёдингер в уравнение (16) ввёл постоянную Планка ћ исходя из гипотезы Планка, который выдвинул её в 1900 г. Здесь энергия микроскопических объектов (атомов, молекул) может принимать не любые непрерывные, а только определённые дискретные значения [25, с. 15], а это было также несовместимо с видом классических уравнений Максвелла. Этот вывод у него следовал из того, что в случае непрерывных значений энергия электромагнитных колебаний могла доходить до бесконечности как в формуле Релея-Джинса, что в науке получило название «ультрафиолетовой катастрофы». Собственно наличие дискретных уровней следует в нашей теории из наличия существования законов физики для чего необходимо иметь как максимальное значение в виде скорости света, так и минимальное значение в виде постоянной Планка, а общее количество объектов равно c/h=N. Кроме наличия дискретности, Планк был вынужден ввести состояние равновесия распределения колебаний по значениям энергии, которое должно подчиняться закону Больцмана [26, с. 323]. Суть его в том, что количество энергетических состояний, как и общее значение энергии ограничено. В этом случае распределение Больцмана имеет вид:

(21)

где N_i – число частиц, находящихся в состоянии с энергией E_i, А ‒ коэффициент пропорциональности, который должен удовлетворять условию:

(22)

Здесь N ‒ полное число частиц в рассматриваемой системе. Отсюда получается формула окончательного распределения Больцмана:

(23)

Для учёта вероятности распределения Планк использовал формулу:

(24)

Если исходить из строгого исполнения физического экспоненциального закона, то данное распределение просто не может быть вероятностным, так как количество частиц строго ограничено, а экспоненциальный закон исключает изменение объектов в силу того, что изменения, выраженные через дифференцирование или интегрирование, не меняют вида функции (закон также однозначен). Отсюда Планк получил свою известную формулу по распределению средней энергии излучения частоты:

(25)

С точки зрения нашей теории, данная формула получается в динамике взаимодействия замкнутых друг на друга глобальных противоположностей с учётом распада объектов в одной противоположности и синтеза объектов в другой противоположности по экспоненциальному закону (по сути ‒ это закон радиоактивного превращения [27, с. 241]):

(26)

Соответственно мы получаем спектр излучения электромагнитных колебаний с наличием максимума на некоторой частоте. В этом случае поддерживается равновесный обмен между противоположностями с преобразованием кинетической энергии в потенциальную энергию, и наоборот. Отсюда, собственно, и следует идея, по которой масса покоя протона связана с движением элементарной частицы типа позитрона в противоположности. Это фактически узаконил Эйнштейн в ОТО, так как, если в СТО скорость относительна, то в ОТО скорость может относиться только к противоположной системе наблюдения и имеет абсолютное значение, и не может быть относительна, так как на основании неё определяется пространственно-временное искривление, что определяет силовое воздействие через обмен. Если бы пространственно-временное искривление зависело от выбора системы отсчёта, то тогда можно было бы подобрать систему отсчёта с исключением существующего взаимодействия в одной противоположности (системе наблюдения), что не наблюдается. Иными словами, протон уже представлялся бы совершенно другим объектом в зависимости от выбора системы отсчёта, так как взаимодействие было бы совершенно иное. Одновременно движение электрона в нашей системе наблюдения формирует массу антипротона в противоположности. Суть такой симметрии следует из наличия замкнутости глобальных противоположностей друг на друга с отсутствием входа и выхода из такой системы Мироздания, которое исключает чудеса возникновения из нуля и исчезновения в ноль. Здесь соответственно надо учитывать, что благодаря системе иерархии с учётом обратно пропорциональной связи между противоположностями не наблюдается противодействия по циклу один протон и электрон, так как для формирования протона используется взаимодействие через среду с учётом всех объектов Мироздания. С учётом перехода потенциальной энергии в кинетическую энергию, и наоборот, формула Эйнштейна может быть переписана следующим образом:

(27)

Здесь Е – общая энергия корпускулярно-волнового объекта; с – скорость света; М_н – эквивалент массы частицы, с учетом СТО Эйнштейна; М₀ – масса покоя элементарной частицы (электрона); Р₀ – импульс электрона в первой глобальной противоположности; V₀ – скорость в системе координат первой глобальной противоположности; М = Р₀/с – масса покоя частицы в пространственно-временной системе, связанной с первой глобальной противоположностью через скорость света; Р = М₀с – импульс частицы в этой системе координат второй глобальной противоположности. Отметим ещё раз, что суть перехода кинетической энергии в потенциальную энергию, и наоборот, фактически определено наличием СТО и ОТО Эйнштейна.

Тогда . При M₀=1/c имеем, что значение импульса Р=1, отражает общую формулу Мироздания вида ch=1 в замкнутом виде и поэтому фактически выражается через импульс в виде замкнутого обмена (вращения). Такая интерпретация связана с тем, что по эффекту Комптона есть наличие закона сохранения не только энергии, но и импульса. Значение массы покоя М при отсутствии распада также сочетается с замкнутым вращением, так как иначе закон сохранения импульса не получить, и мы имеем равенство: [28, с. 235]. С учётом M₀=1/c получим Соответственно мы имеем закон сохранения импульса . Иными словами, масса в одной противоположности переходит в скорость в другой противоположности, и наоборот, с учётом связи противоположностей через скорость света. Понятно, что при V₀=0 в уравнении энергии Эйнштейна (27) остаётся только импульс сM₀=сh=1, характеризующий элементарную частицу. Если бы не было такого преобразования, то не выполнялся бы закон сохранения импульса, так как при переходе в массу покоя он попросту бы исчезал. В этом случае кинетическая энергия электромагнитной волны никоим образом не могла бы перейти в значение скорости движения частицы и наоборот. А такого явления, как аннигиляция электрона и позитрона с преобразованием массы покоя в электромагнитную энергию, не было бы в силу того, что импульс для электромагнитных волн мог образоваться только из ничего. Отсюда в [1, с. 12-32] мы показали метод вычисления отношения массы протона к массе электрона на основе их отношения с выполнением условия термодинамического равновесия.

Таким образом, предлагаемая логика формирования Мироздания имеет практическое подтверждение при определении масс объектов. Заметим, что в физике это отношение масс протона и электрона не имеет никакого логического обоснования. А сам распад массы протона запретили на основе использования некоего барионного заряда [29, с. 275]. При этом возникает парадокс, связанный с тем, что при слиянии ядер происходит освобождение электромагнитной энергии и, согласно формуле Эйнштейна, эта энергия может быть взята только от массы протонов (напомним, что нейтрон также состоит из протона и электрона), находящихся в ядре. Проблему радиоактивного распада физики предложили решать на основе вероятностного подхода на основе квантовой механики с туннельным проникновением α-частиц через потенциальный барьер из неких ядерных сил. То есть опять пошли по вероятностному пути распада частиц. Более того, было предложено представлять сам протон и нейтрон в виде кварков и глюонов [30, с. 295]. То есть физики фактически «опровергли» идею Ломоносова М. В., на основании которой, из чего объект состоит, на то он и распадается. Напомним, что на мифические кварки и глюоны ни один объект не распадается. Кроме того, физики не смогли объяснить явление холодной эмиссии [31, с. 74]. Так как решать задачи научным образом, как это делаем мы на основе реальных физических законов, у физиков не получилось, они пошли по пути подгонки под результат. Здесь был использован вероятностный подход с наличием туннельного эффекта и применением соотношения неопределённостей Гейзенберга. В этом случае процессы в атоме стали описываться по аналогии с процессами в объёмном резонаторе. Здесь как бы существуют стенки в виде потенциальной энергии, а элементарные частицы описывают между этими стенками волновую функцию, дающую вероятность, и при определённых условиях при небольшой толщине этой потенциальной стенки частицы могут оказываться за ней даже при отсутствии соответствующей энергии (рис. 2). Иными словами, физики отказались от причинно-следственных связей, связанных с физическими законами, и решили имитировать процессы в атоме и ядре через подгонку под результат, используя соответствующие коэффициенты в уравнениях. При этом они в качестве аналогов брали результаты от физических законов, отрицая их наличие в данном процессе. Разберём всю цепочку подгоночных решений при сшивании в квантовой механике.

Как мы уже отмечали выше, чтобы решить проблему отсутствия излучения при движении электрона вокруг протона по классической электродинамике, был предложен вероятностный подход нахождения электрона в атомном ядре. Однако этого было недостаточно в силу того, что нет законов связи вероятности с наличием законов физики, например сил кулоновского притяжения и тогда был бы спонтанный выход электрона за пределы атома. Чтобы как-то оправдать закон удержания электрона в атоме была привлечена формула Луи де Бройля, с учётом опытов Дэвиссона и Джермера, которая говорила о наличии волновых свойств у частицы. Кроме того, Г. П. Томсон (1927) и независимо от него П. С. Тартаковский получили дифракционную картину при прохождении электронного пучка через металлическую фольгу (рис. 3).

Рис. 3. Дифракция электронов через очень тонкий слой серебра

Из этого эксперимента выходило, что на движение электрона оказывают влияние все отверстия в слое. Посчитали, что если бы электрон в каждый момент времени находился в определённой точке пространства и двигался по траектории, он проходил бы только через определённое отверстие и тогда дифракционной картины в принципе быть не могло. Так как нельзя было представить дело так, что какая-то часть электрона проходит через одно отверстие, а другая часть через другое в силу того, что электрон обнаруживается как единое целое, с присущей ему массой и зарядом был сделан вывод, что это несовместимо с представлением о траекториях. Иными словами, на основании этого эксперимента ввели вероятность и отказались от причинно-следственных связей, которые существуют во всех физических законах.

Ошибка физиков здесь в том, что, они не рассматривали взаимодействие элементарных частиц через электромагнитное излучение и поглощение, исходя из запрета, введённого Бором, без которых вообще невозможно представить взаимодействие частиц. Физики представляли частицу как объект одной противоположности (корпускулы), а волновые свойства отнесли к вероятности местонахождения частицы, то есть не учитывали корпускулярно-волновой дуализм как процесс в динамике взаимодействия противоположностей через обмен (излучение и поглощение). А раз есть взаимодействие, то есть и взаимное влияние, при котором надо учитывать и волновые и корпускулярные свойства. При этом они как бы «забыли» что волна Луи де Бройля соответствующей частоты приписывается частице и в состоянии покоя по формуле: f=m₀c²/h=c²=c/h=N. В этом случае волна Луи де Бройля должна состоять только из одной частоты (рис. 4), а это возможно, если волна в пространстве имеет параметры от минус бесконечности до плюс бесконечности, что эквивалентно бесконечной энергии.

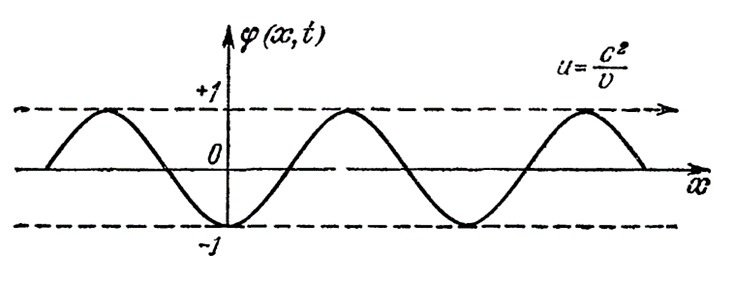
Рис. 4. Волна Луи де Бройля при движении элементарной частицы со скоростью v

Понятно, что для исключения данного варианта необходимо было ввести ограничения, при которых при вероятности нахождения частицы в любом месте (что не наблюдается) было ограничение через закономерности. Поэтому, чтобы оправдать наличие закономерностей при вероятности в 1927 г. В. Гейзенберг «открыл» своё соотношение [32, с. 27]:

(28)

При этом вероятностное местоположение частицы представлялось на основании волнового пакета волн Луи де Бройля, амплитуда которого отлична от нуля лишь в небольшой области пространства [33, с. 23]. Суть соотношения неопределённостей сводилась к тому, что распределение плотности вероятности по переменным принципиально не могут одновременно иметь вид δ-функций. Более того, чем ближе к δ-функции распределение вероятности по одной переменной, тем более размытым становится это распределение по другой переменной. Однако аналог данному соотношению (28) есть и в классической физике в виде E=hf=cp=mc². Отсюда h=pc/f=pcT=px. Соответственно данный закон будет выполняться и для приращений ∆р и ∆х, ∆Е и ∆t, в виде h=∆p∆x=∆pc∆x/с=∆Е∆t. Этот закон фактически означает необходимость обратно-пропорциональной связи противоположностей. Иными словами, ограничения по переменным получаются и без вероятности, а значения скорости света и постоянной Планка определяют возможное количество объектов.

При формировании волнового пакета волн Луи де Бройля рассматривался принцип суперпозиции, когда сумма (или интеграл) частных решений φ_i(x,t) (или их линейная комбинация) также должны быть решением волнового уравнения вида:

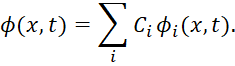(29)

Здесь С_i – некоторые постоянные коэффициенты, которые можно положить равными единице.

Далее предполагается, что волны Луи де Бройля являются линейными, и поэтому для них принцип суперпозиции оказывается справедливым. Следующее допущение касается того, что реальный волновой процесс не может быть чисто монохроматическим (k = const). Он всегда должен обладать определённой шириной, то есть состоит из набора волн, обладающих, например, близкими волновыми числами, а вместе с тем и частотами и вот с помощью такого набора волн строится так называемый волновой пакет (рис. 5).

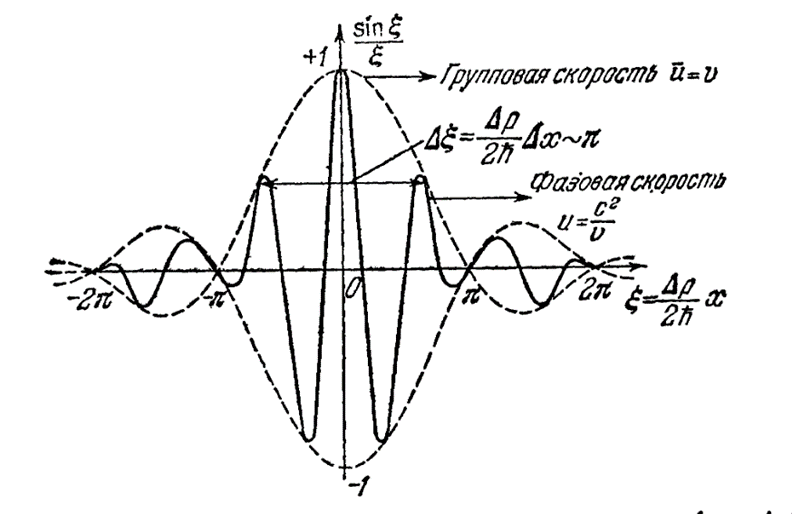
Рис. 5. Форма волнового пакета при t=0 для дебройлевских волн (∆k=∆p/ћ). Амплитуда sinξ/ξ указана штриховой линией, волна сплошной

Если с наличием суперпозиции можно согласиться при наличии волн Луи-де Бройля как волновых функций, определяющих вероятность и неопределённость (отсутствие законов), то существование волнового пакета из волн Луи де Бройля вызывает сомнение, так как волна Луи де Бройля однозначно связана со скоростью движения частицы. В этом случае каждой частоте волны Луи де Бройля соответствует своя скорость движения частицы, ведь волны Луи де Бройля независимы по принципу суперпозиции. Собственно, на этом и строится предположение о «расплывании» волнового пакета Луи де Бройля в атоме. В силу того, что скорость распространения зависит от длины волны Луи де Бройля, то получаем, что волновой пакет «местоположения» элементарной частицы-электрона (m₀~10^-27г) в атоме размерами расплывается со скоростью 10^‒17 с. Иными словами, нет никакого детерминированного движения электрона в атоме, а есть только волновая вероятность. Тогда почему вероятность, исключающая любые законы, должна быть волновым законом, физики не объясняют. Кроме того, отсутствие траекторий у микрочастиц противоречит опытным данным. Так, например, в камере Вильсона путь, по которому движется микрочастица, обнаруживается в виде узких следов (треков), образованных капельками тумана. И здесь явно видно, что имеет место чистая подгонка под результат в случае использовании волновых функций Луи де Бройля, дающих вероятность. Мало того, что вероятность противоречит всем законам физики, но при этом эти волны есть нечто неизвестное, свойства которых придуманы, так как принцип реального воздействия, тем более в виде закономерности волны может быть связан только с реальными объектами (у нас это электромагнитные волны).

Кроме того, судя по рисунку 5 можно заметить, что волновая функция волнового пакета Луи де Бройля имеет как положительные, так и отрицательные значения, а это означает, что если рассматривать функции Луи де Бройля как фактор неопределённости, то вероятность может быть отрицательной. Понятно, что физики также понимали, что это означает явный парадокс. Поэтому на рисунке 1 отразили значение энергии в виде:

(30)

в качестве добавочной постоянной составляющей к волновой функции, исключающей отрицательные значения:

(31)

На основании чего было принято такое решение для совершенно разных величин – неизвестно. Однако и это не решало проблемы, так как с учётом добавления постоянной составляющей к Ψ в виде энергии Е, для Е₂ вероятность слева должна быть выше вероятности справа по рисунку 1. С другой стороны, отказаться от волновой функции физики не могли, так как это вообще бы нарушало понятие совместимости волны с частицей по уравнению Шрёдингера (16). Поэтому они придумали несколько иную интерпретацию для волновой функции Ψ [34, с. 32] на основе уравнения непрерывности исходя из определения плотности заряда (ρ) и плотности тока (j) по формуле:

(32)

С этой целью умножили уравнения Шредингера (16) и (17) соответственно на волновые функции Ψ^*и Ψ и вычли одно равенство из другого:

(33)

Отметим, что это в математике умножение на дополнительные члены и вычитание не влияет на результат. В физике всё иначе, например, вычитание одного из другого уравнений Шредингера, которые характеризуют разные частицы, означает взаимодействие, а всякое взаимодействие ведёт к изменению результата, связанного с переходом в противоположность, так как иначе были бы возможны процессы без взаимодействия противоположностей. Это в математике 5-5=0, а в физике это означает чудо исчезновения объектов, что не наблюдается, даже при аннигиляции электрона и позитрона мы имеем двойную энергию. Такой подход давал бы замкнутость противоположности и никакого корпускулярно-волнового взаимодействия в принципе быть не могло. Кроме того, произведение в уравнении (33) вида Ψ^*Ψ уже изначально даёт значение равное единице даже без интегрирования по всему пространству, то есть константу без волновых процессов в силу вычитания равных аргументов. Это означает, что изменение константы в виде единицы изначально быть не может, тем более что это константа определяет значение заряда типа электрона или позитрона. В итоге из уравнения (33) было получено значение для плотности заряда в виде:

(34)

Здесь e ‒ заряд электрона. Тогда имеем:

(35)

Собственно данный вид был получен и в квантовой механике. Значение для плотности тока представили в виде уравнения:

(36)

При этом посчитали, что в этом случае полученные значения с сопряжёнными волновыми функциями Ψ и Ψ^* удовлетворяют уравнению (32) и, согласно Борну, произведение Ψ(r)Ψ^*(r) следует понимать как плотность вероятности нахождения частицы в точке пространства с радиус-вектором r. Однако предположение, что мы имеем соответствие с уравнением (32) уже изначально ложно, так как заряд элементарной частицы ‒ это константа и не может изменяться во времени, да и произведение волновых сопряженных функций также равно единице изначально (то есть тоже константа), отсюда выражение (33) вырождается в вид:

(37)

Иными словами, вновь имеем чистую подгонку под результат. Понятно, что есть ещё один парадокс, связанный с формулами (30) и (31), так как при n=0, получается вариант с отсутствием энергии и тогда элементарная частица перестаёт существовать и должна произойти аннигиляция с протоном. Действительно для волновой функции (31) при n=0 sin(nπx/l)=0 и значение энергии Е по формуле (30) также равно нулю. Так как в квантовой механике нет механизма, исключающего изменение протона до позитрона, и он состоит из кварков и глюонов, а его распад запрещён барионным зарядом, то нужна энергия, исключающая падение на протон. Напомним, что в нашей теории [1, с. 12-32] такой проблемы нет, так как фоновое электромагнитное излучение в так называемом вакууме из-за наличия констант электрической и магнитной проницаемости, связанных с термодинамическим равновесием между противоположностями есть всегда, и это определяет наличие протона и электрона. По условию термодинамического равновесия, чтобы электрон потерял кинетическую энергию и «упал» на протон, необходимо, чтобы и в противоположности не было бы кинетической энергии. Это возможно, если масса протона сравняется с массой электрона. В квантовой теории в уравнении Шрёдингера и системе уравнений Дирака состояние среды так называемого вакуума в виде констант электрической и магнитной проницаемости не присутствует, и поэтому объяснить наличие нулевой энергии без условия термодинамического равновесия невозможно.

Однако физики обладали хорошими знаниями в математике и поняли, что чтобы избежать отсутствия нулевой энергии необходимо обеспечить в аргументе волновой функции Ψ значение независимое от значения n. Это возможно сделать, но только в том случае, если значение волновой функции не имеет целочисленного значения на границе потенциального барьера в потенциальной яме. Чтобы обеспечить такую подгонку под результат в квантовой механике использовали квазиклассическое приближение. В этом случае для уравнения Шредингера была использована волновая функция:

(38)

Здесь учитывались следующие равенства:

(39)

Поскольку волновая функция Ψ в результате данного преобразования должна входить во все члены лишь множителем, то её в квантовой механике сокращают и получают уравнение:

(40)

Здесь при ћ=0 мы имеем совпадение с уравнением Гамильтона-Якоби, однако с точки зрения физики это бы означало, что минимальные объекты отсутствуют и тогда не должно было быть и законов физики. Если сравнить данное уравнение с классическим уравнением Гамильтона-Якоби для функции действия S в виде:

(41)

Тогда, с учётом взятия производной по времени, имеем:

(42)

В этом варианте видно, что последнее слагаемое пропорциональное постоянной Планка ћ, даст небольшие поправки к классическому уравнению при соблюдении условия:

(43)

Приближение, определяемое неравенством (43), носит название квазиклассического. Принимая во внимание, что p=grad S, последнее уравнение можно записать в виде:

(44)

В частности, для одномерного случая имеем:

(45)

Таким образом, квазиклассическое приближение оказывается достаточно точным в том случае, когда дебройлевская длина волны – величина постоянная или слабо изменяющаяся. Здесь принимается во внимание

(46)

Тогда условие (45) может быть записано в виде:

(47)

где F= ‒∂V/∂x – классическая сила, действующая на частицу.

Отсюда, в частности, следует, что квазиклассическое приближение становится неприменимым при малых значениях импульса частицы и в особенности в тех точках, где по классической теории частица должна остановиться (E=V, р=0). Такое положение имеет место, например, в случае, когда частица, находясь в потенциальной яме, в результате отражения от потенциального барьера начинает возвращаться обратно (точка поворота).

Иными словами, в квантовой механике также признаётся, что чем меньше энергия частицы, тем меньше шансов у частицы выйти за пределы потенциальной ямы. Но вот тут на основании формулы Луи де Бройля (8) и соотношения неопределённостей Гейзенберга в силу обратно-пропорциональной связи между импульсом и волной Луи де Бройля делается вывод, что при р→0, λ→∞, и поэтому волновые вероятностные свойства частицы будут проявляться особенно сильно. Это, собственно, служит оправданием прохода частицы через потенциальный барьер, что получило название туннельного эффекта. Однако, если исходить из такого подхода, то тогда частица при отсутствии движения обладает только волновыми свойствами, и не может иметь точного определения местоположения в принципе, а о формуле Луи де Бройля f=m₀c²/h надо вообще забыть, то есть такая частица не должна иметь взаимодействия через излучение и поглощение и такую частицу обнаружить в принципе невозможно. По сути, это должна быть волна, причём имеющая заряд (что является ещё одним алогизмом), что говорит о наличии постоянной составляющей. Каким образом это волновое образование, да ещё и с отрицательным зарядом будет преодолевать потенциальный барьер при нулевом импульсе остаётся полной загадкой. Более того, это противоречит представлению электрона в виде точечной вспышки на электронно-лучевой трубке.

Действительно, торможение при большой длине волны Луи де Бройля должно приводить к проникновению электрона за экран. Кроме того, этот вариант соответствует одномерной модели, что следует из формулы (47). В варианте движения электрона по дискретной орбите тангенциальная составляющая импульса электрона не равна нулю и постоянна, а значит и волна Луи де Бройля не изменяется и не стремится к бесконечности. Иными словами, переход на одномерную модель уже изначально не может правильно описывать процессы в атоме, так как противоречит наблюдаемым физическим процессам. Не учитывая указанные выше парадоксы, в основу волновой теории в квантовой механике ввели некую дополнительную квантовую потенциальную энергию в виде:

(48)

Понятно, что в квантовой теории эта дополнительная энергия также не имеет объяснения. С точки зрения нашей теории ‒ это энергия противодействия от противоположности. Это связано с тем, что если существует изменение аргумента S (r, t) во времени и пространстве, то это изменение не может происходить без соответствующих противодействующих изменений в противоположности. Иначе противоположности были бы независимы друг от друга и замкнуты сами на себя с отсутствием корпускулярно-волнового дуализма и наличием противоположностей. Следует отметить, что значение ћ характеризует воздействие с другого иерархического уровня противоположности, что исключает замкнутость процессов на одном уровне иерархии противоположностей и требует взаимодействия с учётом всех объектов Мироздания. При этом с учётом нашей теории при m₀=h, получаем: , то есть связь противоположностей через 4π. Отметим, что противодействие организуется отрицательному заряду электрона через положительный заряд протона, где кинетическая энергия подменяется потенциальной энергией.

В данном случае, чтобы перейти от отрицательного заряда к положительному заряду, надо осуществить трёхкратное изменение, так как имеются две глобальные противоположности с независимыми и зависимыми составляющими по нашей теории (отсюда четырёх мерность). Это даёт противоположные заряды, как объекты длины и времени, что также использовано до нас физиками при определении связи силы Кулона и Лоренца по СТО. Трёхкратное изменение обеспечит возведение коэффициента 4π в куб с получением значения (4π)³=1984. А это соизмеримо с разницей между массой электрона (m₀) и протона (1836m₀). Мы же имеем дополнительное подтверждение нашей теории, где замкнутые процессы в одной противоположности рассматриваются как прямолинейные в другой противоположности с преобразованием энергии. Это обеспечивается, за счёт того, что в соответствии с СТО и ОТО Эйнштейна, движение во времени по одной оси координат, рассматривается как замкнутое движение по двум другим осям координат.

Продолжим рассмотрение парадоксов в квантовой механике. Здесь оказалось, что в общем случае решить нелинейное уравнение (42) значительно сложнее, чем линейное уравнение Шредингера. Поэтому многочисленные попытки повести развитие квантовой теории по пути точного решения уравнения (42) успеха не имели. Надо отметить, что в этом случае мы сталкиваемся ещё с одним парадоксом, связанным с тем, что уравнение (42) нелинейное уравнение и значит принцип суперпозиции, который действителен для вероятностного подхода в уравнении Шредингера, в этом случае неприменим. Но как известно математика обладает разными методами подгонки под результат и поэтому Вентцелю, Крамерсу и Бриллюэну удалось, ограничиваясь членами порядка ћ, найти приближённое решение уравнения (42), которое оказалось пригодным для исследования ряда задач квантовой механики методом подгонки под результат. По сути, это есть метод «линеаризации», который, кстати, использовал Дирак при взятии квадратного корня в уравнении энергии Эйнштейна через систему линейных уравнений. Однако при этом для выражения нелинейных процессов взаимодействия он использовал подстановку одних уравнений в другие с применением разных волновых функций, через которые и осуществляется взаимодействие, и учитывал волновые функции по всем координатам, что даёт замкнутые процессы с отсутствием распада частицы. Метод решения со «сшиванием» волновых функций в зависимости от значений энергии, применимый лишь к одномерным задачам, получил название приближённого метода ВКБ. Здесь считается, что потенциальная энергия является гладкой функцией х (рис. 6).

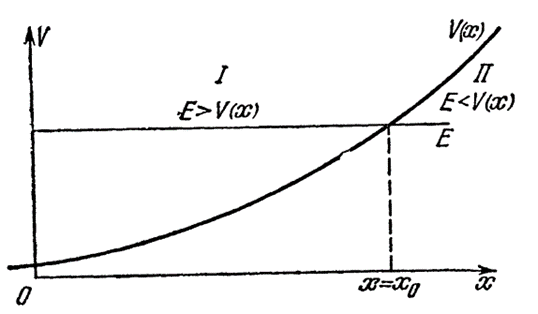
Рис. 6. К решению волнового уравнения по методу ВКБ

Пусть частицы обладают энергией Е, тогда весь промежуток изменения х мы можем разделить на две области. В первой области I (x<x₀) энергия Е больше потенциальной энергии: E>V, а во второй области II (x>x₀), наоборот, E<V. Исходное уравнение (42) в одномерном случае принимает вид:

(49)

Сначала найдём решение этого уравнения для первой области (E>V), когда величина р²>0 играет роль квадрата классического импульса. Решение ищем в виде ряда:

(50)

где величина S₀ не зависит от ћ, S₁ пропорциональна ћ, S₂ пропорциональна ћ² и т. д. Подставляя ряд (50) в уравнение (49) и пренебрегая величинами, пропорциональными ћ² и выше, получаем:

(51)

Приравнивая друг другу члены в левой и правых частях, не зависящие от ћ, а также пропорциональные ћ (при этом необходимо учитывать, что величина S₁ пропорциональна ћ), находим:

 (52)

В этом случае для S’⁰ мы получаем вариант, соответствующий уравнению (41) в виде:

(53)

А это чистое уравнение Гамильтона-Якоби для гармонического осциллятора с объектом массой m₀, на который действует упругая сила.

Иными словами, через аргумент S₀ волновой функции Ψ вида (38) рассматривается движение корпускулярной частицы в потенциальной яме по закону линейного гармонического осциллятора [35, с. 103] в одномерном варианте. Понятно, что мы имеем значение импульса p=0 при x=x₀ (Е=V) и р=2m₀E при x=0 по рисунку 6.

Парадокс такого одномерного подхода в том, что даже если сопоставлять связь противоположностей корпускулярного и волнового вида объекта через значения в аргументе и функции, то в одномерном варианте элементарная частица электрона должна двигаться через протон на основании (53) и такое движение не может обойтись без излучения из-за движения с ускорениями. Именно этот парадокс падения электрона на ядро через потерю энергию через излучение попытался исключить Бор через запрет на излучение при дискретных орбитах. При этом, при минимальной энергии по рис. 1 плотность вероятности нахождения электрона будет как раз в районе нахождения протона. Отметим также, что если бы волновая функция Ψ не соответствовало бы реальности некоторого действия по движению частицы, то что-либо получать из неё не было бы смысла. Нельзя описывать процессы, опираясь на чудеса. Соответственно в силу того, что значение dS₀ /dx=p имеем:

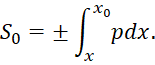(54)

Отметим, что в данном варианте уравнения (53) есть явное несоответствие с принятым изначальным уравнением (51), так как импульс р имеет однозначную связь с S₀. Второе уравнение вида:

(55)

определяет зависимость S₁ от импульса р через S₀. Однако по равенству (53) оно в значение импульса никакого вклада не несёт, так как в (51) по второму уравнению в (52) мы имеем взаимную компенсацию. Далее отметим, что отказ от двумерной модели орбитального движения привёл также и к смене результата; так для гармонического осциллятора в двумерном варианте мы имеем формулу [36, с. 492]:

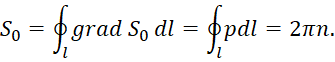(56)

Иными словами, значение S₀ для каждого дискретного уровня ‒ это константа и соответственно при n=0, S₀=0, мы вновь получаем отсутствия энергии у электрона согласно (30). Чтобы получить орбитальное движение электрона с наличием импульса в тангенциальном направлении по уравнению Гамильтона-Якоби (53) необходимо, чтобы V=0. Тогда волновая функция будет соответствовать уравнению Шредингера . При этом будет соблюдаться соответствие по скорости между корпускулярным и волновым движением для волны Луи де Бройля в случае орбитального движения. Однако переход даже на двумерное решение, без парадоксов одномерного решения, показывает, что на основе одного уравнения Шредингера задачу отсутствия потери энергии за счёт излучения (без учёта среды с константами электрической и магнитной проницаемости и замкнутой системы обмена на основании четырёхмерного пространства как в системе уравнений Дирака) не решить. Иными словами, должно быть восполнение энергии излучения. Восполнить энергию излучения в данной противоположности возможно за счёт аналогичного излучения в другой противоположности, так как распад в одной противоположности означает синтез в другой противоположности. В противном случае Мироздание из двух глобальных противоположностей ‒ это не константа с законом сохранения количества и тогда возможны чудеса без каких-либо законов физики. Иными словами, мы будем иметь баланс в излучении и поглощении на основе двух уравнений Шредингера при сокращении на волновые функции Ψ, характеризующие симметричные движения двух объектов в противоположностях (иначе не будет баланса) вида:

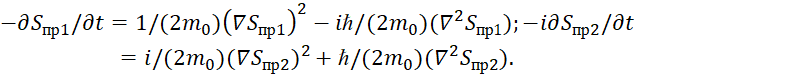(57)

Не надо думать, что физики не пришли к аналогичному виду. Так для описания собственного магнитного момента электрона необходимо было ввести по предположению физиков четвёртое квантовое число, которое должно характеризовать внутренние свойства электрона [37, с. 273]. Однако волновая функция Ψ частицы может зависеть только от трёх квантовых чисел, соответствующих квантованию трёх пространственных координат. Для описания спина и введения четвёртого квантового числа Паули вводит вместо одной волновой функции Ψ, две волновые функции Ψ₁ и Ψ₂. При этом он считал, что одна волновая функция будет описывать состояние с одним направлением спина, а другая с противоположным; само же волновое уравнение должно представлять собой систему двух уравнений:

(58)

Но и здесь очевиден парадокс, при которой возможна неоднозначность волновой функции, когда одной и той же частице должны соответствовать две волны Луи де Бройля. В нашем случае такого парадокса нет, так как здесь рассматривается взаимодействие противоположных частиц, что может быть представлено при корпускулярном движении в виде:

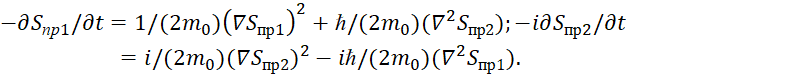(59)

Понятно, что в общем случае для учёта влияния всего Мироздания на данную частицу, член вида должен учитывать влияние противодействия от всех объектов Мироздания, что характеризуется как значение V. Отметим, что направление противодействия выражается не в направлении действия силы, а в перпендикулярном направлении, что исключает компенсацию с наличием нуля и это отражено через силу Лоренца и силу Кулона. Следует отметить, что, таким образом, наша теория позволяет обосновать операцию умножения потенциальной энергии на волновую функцию Ψ и использования постоянной ћ для смены уровня иерархии в уравнении Шредингера. Однако физики решили пренебречь парадоксами при одномерном решении, и, ограничиваясь членами порядка ћ, получили:

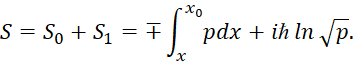(60)

Далее подставили (60) в (38) и нашли следующее выражение для волновой функции в области I (х<x₀) по рисунку 6:

(61)

где

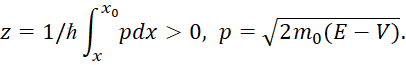(62)

Точно также для области II (x>x₀) в которой р²<0, получаем:

(63)

где

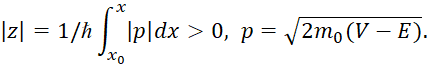(64)

В случае, если потенциальный барьер будет слева от особой точки х₀, то при определении z и |z| необходимо поменять местами пределы интегрирования так, чтобы нижний предел был меньше верхнего. Таким образом, величины z и |z| всегда будут положительными. При этом предполагается, что постоянные а, b, А и В, и фазы и не являются произвольными, поскольку они должны быть связаны определёнными соотношениями, вытекающими из условия сшивания решений вблизи точки х=х₀ при переходе из области I в область II. Однако оказалось, что решения (61) и (63) дают хорошее приближение лишь для областей, сравнительно удалённых от особой точки х₀, где величина р² относительно велика. Вблизи же особой точки величина (х→х₀) величина р²→0, и поэтому знаменатель в выражениях (61) и (63) обращается в ноль, а само решение становится расходящимся.

Иными словами, попытка получить решение задачи на границе особой точки при начальном одномерном варианте методом ВКБ не дало необходимого сшивания в силу того, что значение импульса превращается в ноль и здесь неопределённость нахождения частицы с точки зрения вероятностной квантовой механики должна равняться бесконечности по одномерной координате. Но для математики нет ничего не выполнимого, и решение по сшиванию продолжили. При этом предположили, что если выразить постоянные А и В, через a и b, то найденное приближение было бы вполне достаточным для многих задач, так как область |х-х₀|→0 является сравнительно узкой. Однако соотношение между этими коэффициентами может быть найдено только в результате сшивания функций, которое следует производить именно на границе областей, то есть в точке х=х₀, при этом под сшиванием понимается приравнивание на границе области х=х₀ волновых функций и их первых производных. Так как обеспечить сшивание функций в особой точке х=х₀ не представляется возможным, то пошли опять по принципу приближённых решений и заменили функции, стремящиеся к бесконечности на функции, стремящиеся к нулю в районе особой точки (вот только забыли объяснить: почему бесконечность развернули на нуль), при этом в остальных значениях х функции по виду должны совпадать. Вот где истинно произвольное применение математических методов – «что хочу, то и ворочу», лишь бы устраивал результат.

Продолжим. С этой целью приближённое выражение для Ψ необходимо представить в таком виде, что при больших р² имело место соотношение (61), а при х→х₀, когда:

(65)

Приближённое решение удовлетворяло бы уравнению:

(66)

где постоянная величина ɑ имеет вид:

(67)

Понятно, что таким образом мы изменили и исходное уравнение Шредингера, которое выражалось при х<х₀ в виде:

  (68)

где

(69)

Иными словами, заменили его линеаризованным уравнением, зависящим от значения х. Следует обратить внимание, что аргумент S в функции Ψ перестал соответствовать виду (60) и уравнению (40) и за исходное было принято уравнение (68). Соответственно в уравнении (66) убирается нормировка, связанная с импульсом, а вместе с этим исчезает и связь с волной Луи де Бройля. То есть такая замена приводит уже к несоответствию между корпускулярным и волновым движением частицы, и вряд ли её можно считать правомерной с точки зрения закона любого физического процесса. Кроме того, в особой точке х=х₀ уравнение (66) в области сшивания вместо бесконечности должно давать ноль (вопрос мы уже поставили выше). Так что сшивать при нуле нечего. Снова имеем дело с произвольной подгонкой под результат, и чтобы обеспечить такое сшивание вместо х ввели новую переменную с изменением размерности:

(70)

Тогда уравнение (66) принимает вид:

(71)

Соответственно в этом случае меняется и решения для волновых функций. В этом случае линейно независимыми решениями уравнения (71) являются так называемые функции Эйри и [38, с. 59], которые можно представить в виде следующих интегралов:

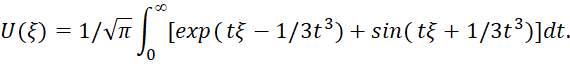(72)

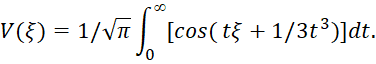(73)

Далее утверждается, что эти интегралы действительно удовлетворяют уравнению (71). С этой целью подставляют второй интеграл (73) в уравнение (71) и, изменяя порядок дифференцирования и интегрирования, получают:

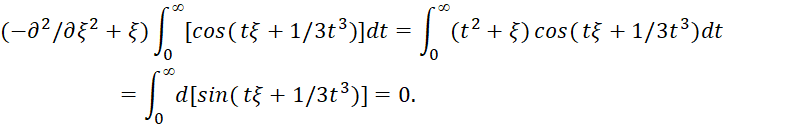(74)

Причём последний интеграл следует понимать как предельное значение:

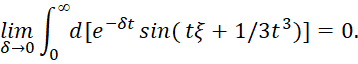(75)

Аналогично подстановка первого интеграла (72) в уравнение (71) показывает, что и в этом случае оно также удовлетворяется. Однако отметим, что в математике рассматривается независимость времени и длины, поэтому можно менять местами интегрирование и дифференцирование. В физике в соответствии со связью длины и времени по СТО и ОТО Эйнштейна этого делать нельзя, так как всякое действие связано с переходом в противоположность на соответствующий уровень иерархии. В противном случае был бы возможен вечный двигатель по замкнутому циклу. То есть в одномерном случае даже с учётом приближений мы сталкиваемся с нарушением законов физики. Но продолжим анализировать метод ВКБ. Асимптотическое выражение функций Эйри и при имеет в случае вид:

(76)

(77)

То есть функция является экспоненциально убывающей с ростом , а функция ‒ экспоненциально возрастающей. В случае же больших отрицательных значений функции и являются осциллирующими:

(78)

(79)

А вот дальше вычисляются значения z и |z| в равенствах (61) и (63) для функций Ψ при х→х₀-0 и х→х₀+0 путём замены значения импульса р на в виде:

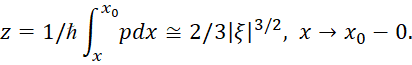(80)

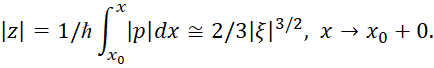(81)

После такой замены следует вывод, что поскольку решения (76-79) и решения (61, 63) должны совпадать в тех областях, где они одновременно справедливы, то приравнивая оба асимптотических решения, получают коэффициенты:

(82)

То есть сам принцип подгонки с заменой переменных в районе особой точки был ориентирован на то, чтобы выразить коэффициенты А и В через a и b, а значения и выразить через фазовое значение π/4. Однако, при общей симметрии между решениями (61) и (63) возникает асимметрия на ½ для коэффициента А, что не имеет объяснения. Кроме того, значение в районе особой точки должно как бы равняться нулю, что исключает представление в виде постоянных коэффициентов а и b. Далее, полагая в равенствах (61) и (63) b=0, а≠ 0 находят первую пару сшитых решений:

(83)

(84)

где экспоненциально убывающее решение (84) в области х>x₀ представляет собой аналитическое продолжение синусоидального решения (83) для области х<x₀. Чтобы определить аналитическое продолжение экспоненциального решения при х>х₀, полагают а=0, b≠0. Тогда для второй пары сшитых решений имеют:

(85)

(86)

Парадокс здесь в том, что это в математике можно убрать одно из решений, в физике, где присутствует наличие детерминированных законов, не может быть неопределённости (неоднозначности), и нельзя произвольно, что-либо «добавить» или «убрать». Кроме того, мы вновь сталкиваемся с наличием роста функций Ψ около особой точки при р→0 до бесконечности, а это также противоречит физике. Далее по полученным формулам осуществляется квантование частицы по энергетическим уровням при нахождении в потенциальной яме в приближении ВКБ. При этом предполагается вариант потенциальной ямы по рисунку 7.

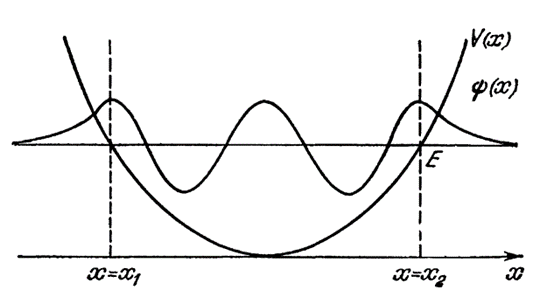
Рис. 7. Квантование потенциальной ямы по методу ВКБ

В данном случае процесс квантования по методу ВКБ будет заключаться в нахождении таких условий, при которых экспоненциально возрастающее решение с обеих сторон потенциального барьера (х<x₁ и х>х₂) обращалось бы в ноль. Тогда, согласно (83) волновая функция в области потенциальной ямы, прилегающей к границе барьера, имеет вид (х→х₂):

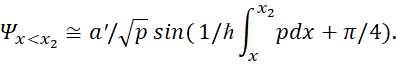(87)

Точно так же для области потенциальной ямы, граничащей с другим барьером х=х₁ , можем написать:

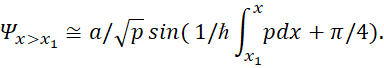(88)

Оба решения должны быть тождественны между собой в любой точке x₁<x<x₂ потенциальной ямы, лежащей на достаточно большом расстоянии от границ потенциальных барьеров. Произведя в одной из точек х сшивание обоих решений (87) и (88), то есть приравнивая в этой точке волновые функции и их производные, имеют:

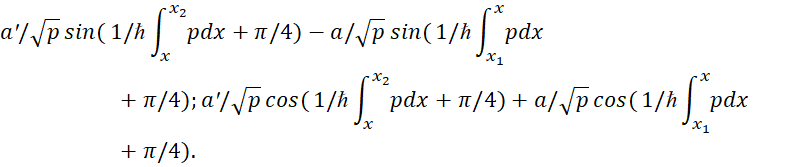(89)

Чтобы эта система однородных уравнений имела ненулевое решение, необходимо выполнить обращения в ноль её определителя. Тогда получают соотношение:

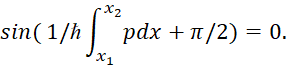(90)

Так как не может быть отрицательной величиной в силу того, что , находят:

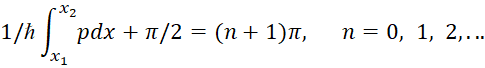(91)

Таким образом, правила квантования, полученные с помощью приближённого метода ВКБ, то есть с точностью до членов порядка ћ, принимают вид:

(92)

Понятно, что при этой подгонке под результат мы имеем всё те же парадоксы. На рис. 7 отражена не функция Ψ, а некая функция φ с наличием добавочной константы в виде энергии Е и без учёта роста в бесконечность в особых точках в зависимости от импульса р. Само же наличие нулевой энергии связано с тем, что в особых точках допускается значение волновой функции Ψ не равной нулю из-за члена π/4 по формулам (87) и (88), как это видно из рисунка 7. Но одномерное решение задачи изначально даёт парадокс с наличием р→0, а это означает что неопределённость растёт до бесконечности и по сути электроны должны свободно перемещаться между атомами игнорируя какие-либо потенциальные барьеры. Следует обратить внимание, что в теории Бора с наличием двумерного варианта при движении электрона на дискретной орбите с наличием р→0 парадоксов нет, так как всегда присутствует тангенциальная составляющая, и здесь с учётом шага квантования ћ имеем формулу:

(93)

Однако здесь имеется проблема падения электрона на ядро при n=0, что связано с тем, что не учитывается равновесный термодинамический обмен между противоположностями с наличием самих противоположностей. Вариант же ВКБ фактически запрещает исчезновение атома, состоящего из электрона и протона из-за наличия «вечной» энергии при n=0, но здесь возникли свои парадоксы, которые мы показали выше. Кроме того, в реальности масса протона уменьшается до массы позитрона с последующей аннигиляцией с электроном, что происходит в нейтронных звёздах.

Отметим, что это ещё не вся подгонка под результат, осуществляемая в методе ВКБ. Далее ищется значение нормировочного коэффициента а и соответственно не учитывается его связь со значением , и что в особой точке эта величина равна нулю. В этом случае при нахождении нормировочного коэффициента в квазиклассической волновой функции ограничиваются интегрированием по интервалу х₁<x<x₂ (потенциальная яма), поскольку вне его волновая функция экспоненциально убывает. Тогда имеют:

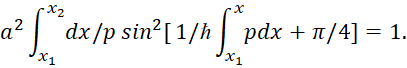(94)

Считается, что синус представляет собой быстро осциллирующую функцию, и поэтому его квадрат, с достаточной степенью точности, можно заменить средним значением, равным ½. Фактически это означает распределение вероятности, полученной от возведения в квадрат в виде значения ½, то есть физически волновой вид вероятности исключается. В этом случае равенство (94) приводится к виду:

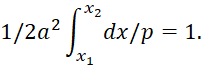(95)

Далее вновь возвращаются к волновому виду, и учитывается, что период колебаний τ=2π/ω равен

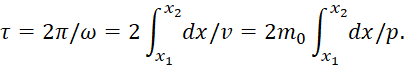(96)

где v=p/m₀ – скорость частицы.

Отсюда для нормировочного коэффициента получают выражение:

(97)

В этом случае собственная функция в приближении ВКБ через подгонку под результат может быть записана в виде:

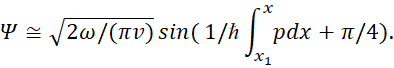(98)

Если исходить из связи импульса и длины волны по формуле Луи де Бройля λ=сТ=с/f=h/р, с учётом нашей теории при m₀=1/c (это даёт f=сv), то получим:

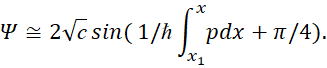(99)

Иными словами, убрали за счёт коэффициента a переход в бесконечность в особой точке при р→0, однако как быть с необходимостью зависимости волновой функции от энергии по рисунку 1 при сшивании? Здесь по (99) функция в месте сшивания от энергии не зависит, то есть мы имеем одинаковый уровень функции при разных значениях энергии и импульса. Кроме того, нормировочный коэффициент оказывается обратно-пропорционален импульсу, который соответствует волновому виду при одномерном варианте и это противоречит усреднению, проведённому в (94) с получением (95) в виде коэффициента 1/2. Понятно, что в этом случае туннельный эффект, связанный с прохождением электрона через потенциальный барьер по полученной волновой функции не зависит от энергии электрона, что противоречит экспериментам.

Таким образом, отказавшись от дискретных орбит движения электрона вокруг протона, которые использовались Бором с отсутствием излучения, квантовая механика за счёт вероятности местонахождения частицы методом подгонок смогла, как бы найти наличие нулевой энергии и оправдать прохождение частицы через потенциальный барьер. Однако при этом такое доказательство дало множество других парадоксов, что было нами показано выше. В результате следует вывод о том, что подгонки под результат, выполненные по методу ВКБ не соответствует физике наблюдаемых процессов. Понятно, что студенты, проходящие обучение по курсу вероятностной квантовой механики, не в состоянии разобраться в таком обилии противоречий, так как не знают иного способа решений, которое было приведено нами в статьях [1, с. 12-32; 2, с. 6-17; 9, с. 3-23; 11, с. 10-24; 18, с. 40-56; 19, с. 32-58; 21, с. 15-30]. Соответственно они вынуждены не анализировать, а верить, что означает, что как специалисты они не будут способны дальше развивать науку, при опоре на очевидную фантастику. Именно поэтому мы так подробно разбираем парадоксы квантовой механики и физики в своих материалах, и продолжим эту работу в дальнейшем.