Топологический метод формирования системы контрольных уравнений в энергораспределении

Подход к формированию системы контрольных уравнений с использованием топологического метода основан на анализе структуры измерений и их расположения в схеме сети. Важно исключить неизмеренные переменные из системы уравнений состояния энергораспределения, чтобы обеспечить полноту и точность контрольных уравнений. Для этого каждый неизмеренный поток энергии в уравнении состояния должен быть выражен через измеренные и расчетные величины. Когда все переменные в уравнении становятся измеренными или могут быть вычислены через измеренные данные, данное уравнение превращается в контрольное уравнение.

В работе [1, с. 53] предложен следующий подход к топологическому формированию системы контрольных уравнений. Сначала строится трехцветный граф, где вершины первого цвета соответствуют уравнениям, вершины второго цвета - измеряемым переменным, а вершины третьего цвета – неизмеряемым переменным. Если переменная (измеряемая или неизмеряемая) входит в уравнение, это отображается на графе добавлением ребра между уравнением и переменной. Затем на основе графа составляется паросочетание, где каждой вершине уравнения ставится в соответствие только одна вершина неизмеряемой переменной. Паросочетание, в котором используются все вершины уравнения или неизмеряемой переменной, называется максимальным [2, c. 72].

Результаты определения максимального паросочетания могут быть следующими:

1. Все уравнения соответствуют неизмеряемым переменным, и остаются неизмеряемые переменные. Эти переменные невозможно вычислить, так как они являются ненаблюдаемыми. В этом случае системы контрольных уравнений нет.
2. Все уравнения соответствуют всем неизмеряемым переменным, что обеспечивает наблюдаемость, но системы контрольных уравнений также нет.
3. Все неизмеряемые переменные соответствуют уравнениям, а уравнения остаются. Все переменные являются наблюдаемыми. Количество оставшихся уравнений определяет количество контрольных уравнений.

Процесс формирования структуры системы контрольных уравнений эненргораспределения приведён ниже (рис. 1).

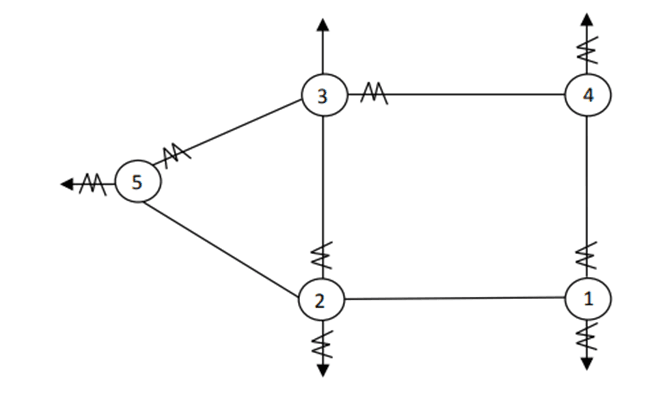
Рис. 1. Пятиузловой фрагмент сети

Трехцветный граф, структурированный для двухмерной системы измерения приведён ниже (рис. 2). Вершины, соответствующие уравнениям состояния: (w1, w2, w3, w4, w5).

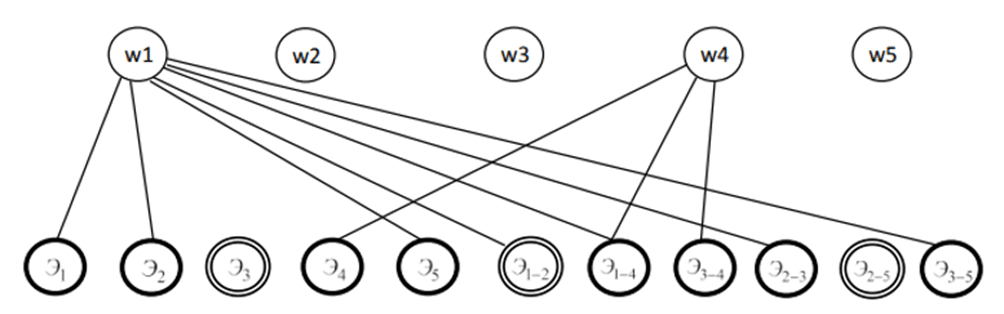
Рис. 2. Трехцветный граф для фрагмента сети (рис. 1)

Вершины, соответствующие измеренным переменным: (Э1, Э2, Э4, Э5, Э1−4, Э3−4, Э2−3, Э3−5). Вершины, соответствующие неизмеренным переменным: (Э3, Э1−2, Э2−5). Максимальное парасочетание: (w1 − Э1, Э2, Э5, Э2−3, Э1−4, Э3−5), (w4−Э4, Э1−4, Э3−4). Таким образом, при данной топологии сети, подобное количество и расстановка измерений обеспечивает наблюдаемость ЭР, а также наличие двух КУ.

Выявление измерений с грубыми ошибками на основе метода КУ состоит в процедуре сравнения невязок k –го КУ wk с допустимым отклонением dk:

(1)

Небаланс (невязка) k-го КУ рассчитывается с использованием значений данных измерений Эi:

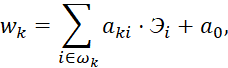(2)

где – коэффициенты при переменных линеаризованного контрольного уравнения; – свободный член контрольного уравнения. В случае, когда ни одно измерение не содержит ошибок, небаланс КУ равен нулю. Допустимое отклонение для k-го КУ рассчитывается по формуле:

(3)

в которой – общее среднеквадратичное отклонение (СКО) КУ, равное сумме СКО всех измерений ЭЭ, входящих в k -е КУ:

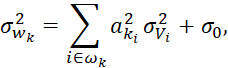(4)

где − постоянная величина, с помощью которой учитывается погрешность линеаризации. Величина γ определяет вероятность того, что при полученном значении допустимого порога dk в составе КУ нет плохих данных. Следовательно, величина допустимого отклонения dk определяется значениями дисперсий измерений, входящих в k-е КУ. Абсолютная погрешность измерения ЭЭ составляет:

(5)

где – относительная погрешность ИКЭЭ, вычисляемая описанным ранее методом. Абсолютная погрешность больше дисперсий измерений в γ раз. В формуле (4) значения коэффициентов определяются по следующему алгоритму: если согласно измерению, ЭЭ поступает на объект, то коэффициент равен «+1», в обратном случае, когда происходит отпуск ЭЭ с объекта, величина равна «-1». Величина допустимого отклонения КУ будет определяться по формуле:

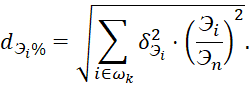(6)

Формула (6) аналогична выражению для расчета допустимого небаланса ЭЭ (6), поскольку величина поступающей на энергообъект ЭЭ незначительно отличается от величины отпущенной ЭЭ, Эо ≈ Эп.

Таким образом, предложенный метод достоверизации измерений электроэнергии на основе балансового подхода представляет собой сравнение фактических и допустимых небалансов с целью выявления грубых ошибок. Данный подход аналогичен методу использования системы контроля управления (СКУ), где проводится сравнение невязки уравнения с заданным порогом. Допустимые значения порога и небаланса определяются на основе предельно допустимых погрешностей приборов учета, а фактические значения небаланса и невязки в расчете основаны на измерениях, включенных в данное уравнение. Этот метод позволяет эффективно контролировать и корректировать точность измерений электроэнергии, обеспечивая более надежный учет и управление энергетическими ресурсами.