Доказательство необходимости наличия живых существ в биологии необходимо с целью понимания использования способов и методов по продлению нашей жизни и её качества. Вот уже на протяжении многих столетий учёные пытаются разгадать эту загадку. Необходимо отметить, что Больцман в 1886 г. попытался с помощью энтропии объяснить, что такое жизнь. По мнению Больцмана, жизнь ‒ это явление, способное уменьшать свою энтропию. «Всеобщая борьба за существование ‒ это борьба против энтропии». Согласно Больцману и его последователям, все процессы во Вселенной изменяются в направлении хаоса. Вселенная идет к тепловой смерти. Этот мрачный прогноз долго господствовал в науке. Понятно, что изречение Больцмана не даёт объяснение возникновению живых существ, так как не ясен сам принцип необходимости или отсутствия изменения энтропии в ту или иную сторону. Энтропия по формуле Больцмана имеет количественную характеристику, а как объяснить уменьшение энтропии? Понятно, что для уменьшения энтропии должны быть закономерности, которые давали бы противодействие, через которые как раз и характеризуются живые существа. Однако сравнение по возрастанию или уменьшению можно вести только при сопоставлении количественных характеристик, но как это сделать? Вот тут как раз и требуется опора на законы теории мироздания [1]. Как мы отмечали при выводе теории мироздания из одной аксиомы об отсутствии чудес, любой объект Мироздания описывается через две глобальные противоположности. Причём если в одной противоположности некий процесс описывается через сложение (синтез), то в другой противоположности он должен представляться в виде вычитания (распада), так как в противном случае нет разницы и отличий между противоположностями. С учётом закона сохранения количества (в противном случае законы физики будут отсутствовать и должны быть чудеса) общая формула мироздания имеет вид:
А + В =С-D= const (1)
Иными словами, синтез в одной противоположности должен сопровождаться распадом в другой противоположности, и наоборот, при неизменности и вечном существовании мироздания. Иное означает чудо возникновения из ничего и противоречит наличию любых законов физики, что не наблюдается. Здесь константа мироздания не может быть ни нулём, ни равняться бесконечности, так как ноль – это отсутствие мироздания, а бесконечность исключает наличие законов физики с учётом действия и противодействия (в этом случае нет констант мироздания и возможна, например, «ультрафиолетовая катастрофа» с исключением СТО и ОТО Эйнштейна). Однако по математике равенство (1) можно получить только при константе равной нулю, а это означает, что, чтобы соответствовать наличию противоположностей в мироздании помимо описания в виде количества, должно быть описание в виде качества (закономерностей) в виде:
cos2(x)+sin2(x)=ch2(w) – sh2(w) =1= const,
exp(ix)exp(-ix)=exp(w)exp(-w) =1. (2)
Здесь атрибут i=(-1)1/2 характеризует принадлежность к противоположности, который при возврате в противоположность оказывает противодействие. Доказательство необходимости такого подхода с математическим представлением подробно описано нами в [2, с. 42-61]. Из формулы (2) также следует, что невозможно отделить наличие любого объекта, выраженного количественно, без соответствия некоторой закономерности. И это как раз и определяет связь количества с качеством, что было отмечено в качестве постулата в диалектическом материализме. Иными словами, как только мы пытаемся отделить количественную характеристику любого объекта от его закономерности (качества), то мы однозначно нарушаем формулы (1) и (2) с исключением существования самого мироздания и приходим к чудесам. Именно эту ошибку допускали учёные, когда подразумевали воздействие случайного внешнего процесса на некоторое количество объектов при формировании живых существ, что будет показано несколько ниже. Однако, если количество определяет наличие объекта как единого целого в виде корпускулы, при условии отсутствия распада, то закономерность невозможно рассматривать без воздействий через обмен с другими объектами, так как иное означало бы полную замкнутость объекта. То есть, влияние закономерности выражается через кинетическую энергию в виде волновых свойств, которая меняет характеристики объектов. Соответственно, при отсутствии распада объекта, закономерность объекта, определяющая обмен, однозначно соответствует количественной характеристике этого объекта в динамике взаимодействия. Одновременно, наличие противоположностей с сохранением количества и представление процессов в зависимости от места наблюдения, подразумевает симметрию, и кинетическая энергия (волновая электромагнитная энергия) в одной противоположности представляется потенциальной энергией (корпускулярная энергия) в другой противоположности. Это взаимодействие с переходом от волновых свойств к корпускулярным мы показали в [3, с. 32-58]. Соответственно представить количественные и качественные характеристики объектов вне представления кинетической (электромагнитной) энергии и потенциальной (корпускулярной) энергии невозможно, так как нет выполнения СТО и ОТО Эйнштейна. Иными словами, воздействие закономерности в виде кинетической энергии в одной противоположности имеет корпускулярный (количественный) вид в другой противоположности в силу того, что состояний энергии только два в уравнении энергии Эйнштейна для описания любого объекта. Отсюда, как энтропия (случайный процесс), так и целенаправленное воздействие, имеет описание через количественные характеристики, то есть через энергию противоположностей, так как ничего иного и нет. Одновременно формулы (2) исключают рост энтропии до бесконечности, что было в формуле Больцмана и давало тепловую смерть Вселенной. Формулы в (2) равняются константе и характеризуют слева и справа от знаков равенства противоположности с наличием симметрии и сменой корпускулярных и волновых свойств. Отсюда противодействие одной противоположности на другую соответствует энтропии, так как это приводит к разрушению предыдущего состояния. Одновременно само воздействие каждой противоположности можно рассматривать как целенаправленные действия, которые препятствуют разрушению. Иными словами, энтропия в одной противоположности выглядит как закономерность (информация) в другой противоположности. В замкнутой системе мироздания, выраженной через константу иное и невозможно, и соответственно в дальнейшем мы определим, почему использование формул (2) не приводит к полностью детерминированной системе связи всех процессов в мироздании.
Вначале, попытаемся проанализировать количественные и качественные характеристики по формулам (2) в виде энергетических составляющих, и сопоставить их с известными другими законами, например, с количеством информации и энтропией в абстрактной двоичной системе булевой алгебры. Почему взято такое сопоставление? Оно следует из того, что ещё Больцман связал энтропию (случайный процесс) с температурой и теплом, то есть количественными значениями в физике (это также отражается через энергию), а из определения академика В. М. Глушкова [4] получается, что «информация ‒ это мера неоднородности распределения материи и энергии в пространстве и времени; мера изменений, которыми сопровождаются все протекающие в мире процессы». Такое определение информации (если убрать из текста понятие материи, которое не имеет даже формулы описания и оставить только энергию, как количественную характеристику) является (как подчёркнуто автором) мерой целенаправленных изменений (неоднородности на основе действия закономерности, что и приводит к изменениям), которыми сопровождаются все проистекающие в мире процессы. Это как раз приводит к уменьшению энтропии по Больцману.
Основываясь на действиях живых существ как информации в виде программных алгоритмов, академик Н. М. Амосов пытался создать кибернетического робота подобного живому существу, но за счёт случайных процессов по выбору алгоритма управления. Однако он потерпел неудачу в силу того, что случайные процессы от одной противоположности не несут никакой целенаправленной информации для другой противоположности в силу того, что в этом случае мы имеем зависимость от аргумента в функциях только от одной противоположности – случайных изменений. Это фактически означает, что мироздание управляется только одной закономерностью (причём любой закономерностью) без противодействия, а это означает наличие чудес. То есть в этом случае мы имеем воздействие от одного общего аргумента в функциях в (2), который не является объектом мироздания, состоящим из противоположностей и который подчиняется закону сохранения количества в силу того, что этот аргумент закономерность. Понятно, что такая свобода выбора закономерности аргумента означает возможность отсутствия динамики изменений в мироздании в силу, например, выбора только одного количественного значения аргумента, что эквивалентно однородности и наличию вечного существования в одной противоположности, что исключает необходимость и самих противоположностей с точки зрения аргумента. Таким образом, чтобы исключить отрицание необходимости противоположностей, нужно обеспечить представление аргументов функций в (2) слева и справа от знака равенства аналогично представлению объектов в виде противоположностей (корпускулярно-волновой вид) с разбиением на зависимые (корпускулярные) составляющие и независимые (волновые) составляющие. Каким образом обеспечивается в этом случае влияние аргументов друг на друга, в сочетании со свободой выбора, мы рассмотрим несколько ниже. Соответственно здесь возникает цель в определении характера и количественных взаимодействий этих составляющих по отношению друг к другу при формировании целенаправленных действий, что характеризует живых существ. Определение правильных количественных соотношений между противоположностями при наличии мироздания как константы требуется и потому, что формула энтропии Больцмана, даёт бесконечность в пределе увеличения энтропии, а это парадокс, который исключает законы физики.
Иными словами, чтобы прийти к выводу о необходимости живых существ по физике взаимодействия надо понять как целенаправленные действия в виде закономерностей (информации) в одной противоположности связаны со случайными процессами (энтропией, хаосом) в другой противоположности. При этом, если исходить из изречения Больцмана по определению живых существ, информация должна быть противоположностью к хаосу.
При определении сущности энтропии и информации не будем «изобретать велосипед», а будем опираться на то, что уже сделано до нас с исправлением очевидных ошибок и парадоксов.
В физике понятие энтропии, истолковывают так же, как количественную меру неопределённости о сообщении до его приёма, то есть как-то количество информации, которое должно быть в среднем получено для опознавания любого сообщения множества Х [5, с. 619]. Соответственно мера изменений в качестве сообщения всегда выражается через количество по отношению к шуму (энтропии). Поэтому проведём эту оценку меры изменений, исходя из анализа физических процессов. Любопытный читатель непременно задаст вопрос: «А почему из анализа физических процессов?» Ведь даже само понятие информации (не по определению В. М. Глушкова) – это сведения, независимо от формы их представления. Иными словами, информация может являться некоторой абстракцией. И вот тут, если следовать математике с её бесконечными изменениями величин, количество информации может быть бесконечно, например, 2H=N→∞ при H→∞. Но это в математике мы можем сталкиваться с неопределённостями типа 0∞, 1/0=∞ и так далее, а в реалиях жизни бесконечные процессы относятся только к замкнутым величинам типа изменений по окружности. Однако хаос через физические величины выразил в своей формуле энтропии ещё Больцман, исходя из наличия неких состояний или событий (Ω), что будет показано несколько ниже, а при замкнутости мироздания, энтропия в одной противоположности должна быть эквивалентна информации (закономерности) в другой противоположности (иначе нет отличий между противоположностями), что также будет нами показано. Кроме того, для существования физических реальных процессов требуется наличие константы в скорость света ‒ с, и минимального шага дискретизации в виде постоянной Планка ‒ h, что было нами показано в [1; 2, с. 42-61]. Иначе была бы возможна «ультрафиолетовая катастрофа», и на действие тут же следовало противодействие из-за мгновенного ответа (скорость света в этом случае бесконечна, постоянная Планка равна нулю), что исключает вообще любое движение. При этом напомним, что если бы скорость света не равнялась константе, и не было бы подчинения при этом СТО и ОТО Эйнштейна, то мы бы имели геометрию Эвклида, вместо геометрии Лобачевского, и тогда замкнутость по координатам длины для объектов без преобразований длины на время, и наоборот, не получить. Таким образом, при дискретности минимального изменения количества в виде постоянной Планка (h) и максимальной скорости в виде скорости света (с), количество информации и соответственно энтропия не могут быть бесконечными величинами, так как количество объектов и их комбинаций соответственно будут иметь ограничения. То есть, замкнутое мироздание на две противоположности имеет формулу ch=1. Собственно аналогом такой зависимости в физике явилась величина постоянной тонкой структуры αпст=2πq2/(hc) =2π/137. При этом заряд q по теории «дырок» Дирака должен равняться ±1 в силу того, что заряд в формулу энергии Эйнштейна (54) не входит. Соответственно максимальное количество объектов определяется в виде числа Nм=c/h, и эта величина связана с постоянной Ридберга. А это исключает возможность количественного представления информации с ростом до бесконечности. Собственно данный вывод подтверждается и наличием формулы Планка, что также будет рассмотрено ниже. Действительно, всё, что мы видим, в том числе и окружающая среда выражается в виде объектов от двух глобальных противоположностей, а эти противоположности имеют количественное ограничение. В противном случае возникают чудеса незамкнутых состояний с возникновением из ничего. Соответственно, как фактор противоположности к энтропии, которая определяется как некое количество, мы должны иметь определение информации, тоже в виде количества. Иначе сравнение просто невозможно. Отметим, что представление информации без физического носителя в виде количественной характеристики не имеет никакого интереса, так как в жизни не может ни оказывать воздействия, ни получать его и изменяться, так как ‒ это ноль. Поэтому, мы связываем количество информации с конкретными физическими носителями (в частном случае с количеством энергии по формулировке В. М. Глушкова), так как даже мысли, которые формируются у нас в мозге, имеют конкретное энергетическое воплощение и не являются неким нулём. Например, пропускную способность канала по передаче информации (а это характеризует закономерность целенаправленных действий от живых существ) определяют по формуле [6, с. 623]:
(3)
где: С ‒ пропускная способность канала, бит/с; F ‒ верхняя граничная частота спектра, Гц; S ‒ полная мощность сигнала в полосе частот F, Вт; N0 ‒ спектральная плотность шума в полосе частот F, Вт/Гц. Это означает, что на практике для оценки информации используются изменения реальных физических величин в виде энергии и спектра.
Кроме того, в соответствии с формулой Хартли количество информации равновероятных событий определяется по формуле:
(4)
Здесь H – количество информации; N – количество возможных событий.
Сам процесс получения информации рассматривается как выбор одного сообщения из наперёд заданного множества равновероятных сообщений. Формула определения количества информации (учитывая возможную неодинаковую вероятность событий) названа в честь её открывателя ‒ Шеннона. Если исходить из теории информации, то имеем алфавит, состоящий из N символов с частотной характеристикой P1, P2, . . . PN, где Pi − вероятность появления i-го символа (или вероятность отдельных событий). Все вероятности неотрицательны и их общая сумма равна 1. Тогда средний информационный вес символа (количество информации, содержащееся в символе) такого алфавита выражается формулой Шеннона:
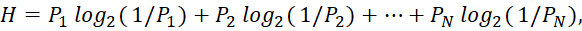(5)
Как будет показано ниже при определении энтропии по Больцману, аналогичный вид формулы имеет и энтропия с учётом физического параметра температуры, исходя из числа способов, которым может осуществиться соответствующее состояние системы. Это совпадение формул с учётом смены переменных соответствует тому, что энтропия в одной противоположности представляется информацией в другой противоположности исходя из замкнутости системы мироздания. Вспомним результаты вычислений энтропии в статистической радиотехнике [7, с. 623] для двух возможных значений случайной величины х: х1=0 и х2=1 (по сути рассматривается замкнутая система). Причём априорные вероятности передачи соответственно равны:
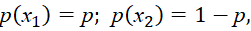(6)
Отсюда находим энтропию по формуле (рис. 1):
(7)
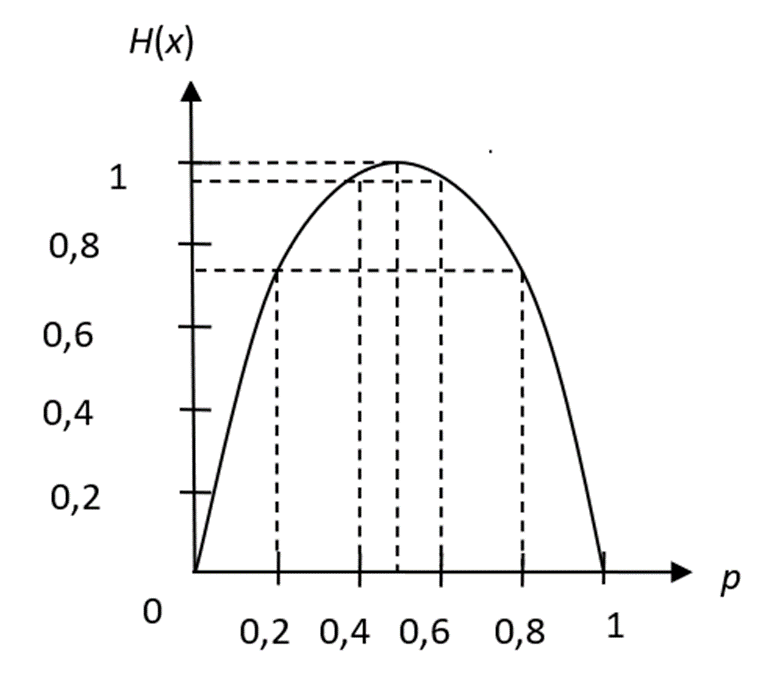
Рис. 1. Энтропия двоичного алфавита как функция вероятности одного из символов
Если энтропия для двух состояний вычисляется по формуле (7), то информация от противоположности будет выглядеть по формуле из [8, с. 624] (рис. 2):
(8)
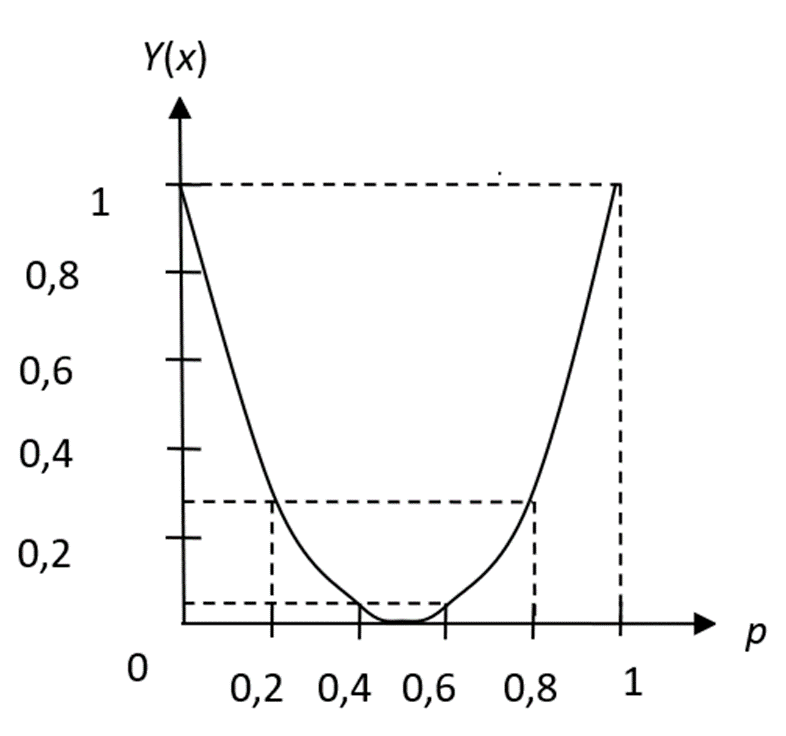
Рис. 2. Зависимость передаваемой информации в двоичном симметричном канале от вероятности ошибки
Соответственно при сложении получим единицу по формуле:
H+Y=1, (9)
где Н – энтропия; Y – информация. Этот вывод количественно был обоснован Бриллюэном. Понятно, что энтропия и информация являются противоположностями, и фактически отображают замкнутую систему. То, что с точки зрения одной противоположности выступает как случайный процесс, с точки зрения другой противоположности означает осмысленный детерминированный информативный процесс.
Соответственно, при Н и Y, которые характеризуют замкнутые друг на друга противоположности, можно расписать по аналогии с учётом представления любого глобального объекта в виде взаимодействия из других объектов:
(10)
Так как физические процессы связаны с выполнением закона сохранения энергии и импульса для любого объекта (и именно эти параметры рассматриваются во взаимодействии любых объектов), то, чтобы связать физические процессы с энтропией и информацией, полученными при двоичной системе, надо иметь на основе, например, закона сохранения импульса - закон эквивалентный формуле (5). Причём в импульс входит как потенциальная энергия в виде массы, так и кинетическая энергия в виде скорости. Как известно, изменение энергии не может быть вне изменения импульса, так как эти величины связаны через скорость света, более того при эффекте Комптона (более подробно об этом в [9, с. 15-30]) пришли к необходимости закона сохранения импульса. Поэтому изменение количества информации представим через изменение импульса Р=mv, в который входят две противоположные величины: масса и скорость, в отличие от формулы энергии в виде Eп=mc2 или Ек=hf. Понятно, что изменения связаны с импульсом, а значит и с изменением в информации и энтропии, так как отсутствие движения означает наличие константы и не несёт никакой информации. Представление массы и скорости как противоположностей мы описали выше в [10], где масса покоя электрона в одной противоположности имеет обратно пропорциональную связь со скоростью света в другой противоположности m0=1/c. Изменение импульса в физике анализируется на основе известного уравнения Мещерского с учётом сохранения импульса объектов.
Отсюда, рассмотрим тело переменной массы М(t). Пусть за промежуток времени dt к телу присоединяется малая масса dm1, имевшая до присоединения скорость v1, и отделяется малая масса dm2, скорость которой после отделения v2. В качестве интересующей нас системы будем рассматривать все три упомянутых объекта. В соответствии с законом сохранения импульса, импульс в начале и в конце рассматриваемого процесса одинаков:
(11)
где d(Мv) ‒ изменение импульса основного тела, как за счёт изменения массы, так и изменения скорости. Учитываем, что:
(12)
Получаем:
(13)
Видно, что изменение dМ основного тела массы связано с изменением dm1 и dm2, то есть:
(14)
Отсюда следуют записи:
(15)
Однако это относится к варианту взаимодействия трёх объектов в одной противоположности (системе наблюдения). В частном случае замкнутого взаимодействия двух противоположностей имеем изменение импульса для двух объектов в виде:
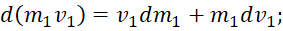
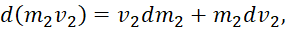(16)
В соответствии с нашей теорией изменение кинетической энергии в одной противоположности равно изменению потенциальной энергии в другой противоположности. Иное бы означало отсутствие отличий между противоположностями, и соответствует переходу от уравнения Мещерского к уравнению Циолковского в виде:
(17)
С учётом того, что учитывается закон сохранения количества между противоположностями, в этом случае М=m2, а v2=0. Такое условие связано с тем, что противоположности замкнуты друг на друга, и не могут отличаться ни по приращениям, ни по количеству. Исчезновение какого-либо количества объектов в одной противоположности означает автоматическое появление их в другой противоположности. При этом должен быть равный переход объектов в прямом и в обратном направлении, так как разница в количестве означало бы наличие объектов только одной противоположности, которые замкнуты сами на себя и тогда их невозможно было бы обнаружить в Мироздании. Это бы означало появление чего-либо из ничего и такое же исчезновение в ничто, а это ‒ чудо. Замкнутые процессы по изменению энергии давно известны в физике. Например, уравнение для идеального газа при изотермическом процессе [11, с. 282]:
(18)
Здесь pд ‒ давление; V ‒ объём. При нашем подходе, объём можно интерпретировать как пространственно-временное искривление (собственно любой объём должен подчиняться СТО и ОТО Эйнштейна), дающее массу, а давление как скорость. Но следует заметить, что физические процессы рассматривались в рамках одной противоположности, что (как это будет видно в дальнейшем) не позволяло связать скорость и массу, чтобы объяснить физику уравнения Шеннона.
При замкнутости противоположностей друг на друга в рамках отдельного объекта по нашей теории (в противном случае объект бы распался), имеем:
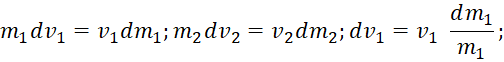
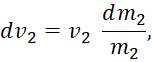(19)
Соответственно, система из двух объектов будет иметь описание в виде:
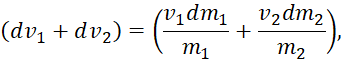(20)
Так как по (dv1+dv2) рассматриваются изменения, связанные с переходом в противоположность, то эти изменения формируют в противоположности величину отличную от прежнего представления в виде скорости. То есть, вектор скорости превращается в некую скалярную величину, по нашей теории ‒ это вектор скорости с проекцией на время, а время – это скалярная величина, причём движение по любой из координат пространства даёт сумму.
Отсюда при интегрировании обеих частей уравнения по соответствующим переменным получим:
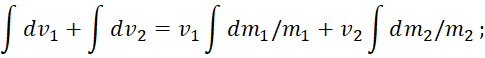
(21)
Так как значения V1 и V2 при проекции на время это не v1 и v2 в силу того, что мы ввели изменение в виде интегрирования и это означает переход на другой уровень иерархии (в математике интерпретируется как добавление некоторой константы). Практически изменение скорости по нашей теории переходит в значение массы, то есть V=1/M, так как по СТО и ОТО Эйнштейна время переходит в другой противоположности в длину, в противном случае нет необходимости во взаимодействии противоположностей. Сравнивая (21) с (5), мы видим, что для совпадения по закону изменения, нам необходимо показать представление скорости и массы как противоположностей, связанных обратно пропорциональной связью. Это можно сделать, если учесть, что противоположности, какими являются скорость и масса в соответствии с уравнениями (19), могут быть разделены и проинтегрированы в виде:
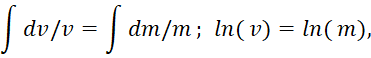(22)
В уравнениях (22) имеем представление количества в двух противоположностях в одинаковом виде, разница только в обозначениях по символам. Иными словами, равенство (22) характеризует равное количественное преобразование в противоположностях при замкнутой системе для каждого объекта и отсутствии распада. При этом, если вести наблюдение из каждой противоположности, то значения v и m будут характеризовать либо значение массы, либо значение скорости. Но величина, отражающая скорость в одной противоположности не может быть скоростью в другой противоположности, иначе отличий между противоположностями нет. В соответствии с этим, и учитывая обратно пропорциональную связь между противоположностями, при отсутствии распада объектов, у нас масса в одной противоположности переходит в скорость в другой противоположности. Это мы показали в [2, с. 42-61; 12, с. 5-26], и в случае отсутствия распада объекта должны записать для противоположных величин равенство:
(23)
Здесь 
, а m отражает скорость в противоположности. Это означает, что в замкнутой системе двух противоположностей (объекты без распада также являются замкнутыми системами), с учётом сохранения количества, масса в противоположности однозначно переходит в скорость, и, наоборот, с выполнением обратно пропорциональной связи между противоположностями. Тогда, если это учесть, с условием закона сохранения количества, так как объект не распадается, и при замкнутости на две противоположности, то можно записать:
(24)
Здесь величина V0 отражает вклад в движение (изменение) от двух объектов. Иными словами, мы получаем эквивалент формул Шеннона (5) и (7) через вносимые объектами изменения. Иного в принципе быть и не могло, так как в обоих случаях рассматривается замкнутая система на две противоположности. Однако, при сравнении с (5), в правой части уравнений мы имеем разницу в значении основания логарифмов. Разница в значении основания логарифма также не является принципиальной, так как известна формула пересчёта:
(25)
При этом натуральная единица информации в 1,443 раза больше двоичной (log2e≈1,443). Разница в основании логарифмов связана с тем, что в системе булевой алгебры с двоичным исчислением отсутствует переход количества в новое качество с иерархией построения мироздания с экспоненциальным представлением объектов. Действительно экспоненциальное представление через (еах) при изменениях меняет уровень иерархии, но не приводит к исчезновению объекта. Надо отметить, что такая же разница в вычислении энтропии в основании логарифма присутствует и в формуле энтропии Больцмана. Иными словами число Эйлера (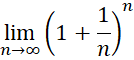
) определяет состояние информации с учётом взаимодействия не только двух объектов, а всех объектов мироздания при условии сохранения объектов. Иное бы означало, что есть объекты, которые не участвуют во взаимодействии, а это ноль, так как их нельзя обнаружить. Действительно в нашем случае масса и скорость объекта выступают как противоположности, и в этом случае для соблюдения закона сохранения количества, при изменениях одна противоположность выступает аргументом изменения (воздействия), а другая - функцией с учётом обратно-пропорциональной связи в виде: 
(аналог в двоичной системе для информации 
). Соответственно при переходе к логарифмическому отображению с учётом аддитивного сложения имеем эквивалент записи H*=M=ln(1/v)=lnN* (аналог в двоичной системе H=log2(N)). Отсюда, с учётом всех значений v, общее значение которых ограничено в силу ограниченного числа объектов мироздания, получается формула; 
.
К виду (7) можно прийти, если рассматривать систему из двух глобальных противоположных объектов, характеризующих всё мироздание. При этом в замкнутой системе с учётом нормировки на скорость света нужно осуществить переход к величинам меньшим единицы в виде:
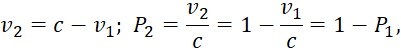(26)
Отсюда имеем:
(27)
Таким образом, через формулу (27) мы имеем представление объекта в мироздании через две противоположности. Полное соответствие с формулой (7) с переходом к двоичной системе мы получим при очередной нормировке величин в виде:
(28)
Собственно разница с (5) лишь в том, что мы заменили вероятность, на значения детерминированных процессов по изменению в мироздании за счёт влияния противоположностей друг на друга. То есть, при ограниченном количестве объектов во вселенной и замкнутости двух глобальных противоположностей друг на друга при представлении мироздания как константы, мы при соответствующей нормировке, также имеем единичное значение по формуле (9). Причём мы исключаем вероятность как аналог чудес, а хаос – это результат целенаправленных действий от другой противоположности для обеспечения сохранения мироздания как константы. Теперь нам осталось связать вероятности, выраженные по формуле (7), с уравнением по пропускной способности информации вида (3), которое выражено через энергетические характеристики шума и сигнала. Исходя из этого, запишем:
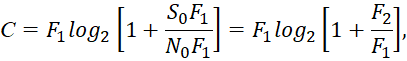(29)
Вспомним, что волна Луи де Бройля (а это подтверждено экспериментом) связана со скоростью движения. Как мы показали в [13], данный вывод может быть получен на основании формулы Луи де Бройля, которая также выводится из аргумента волновой функции с учётом связи длины и времени через скорость света, что, собственно, ввёл Г. Минковский [14] r=ct=c/f в виде:
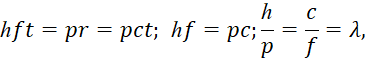(30)
В итоге мы получим с/fд=1/(hfд)=λд=1/v. Это означает, что частота и скорость движения эквивалентны в противоположностях. Понятно, что размерность здесь не соблюдается, но мы имеем дело с количественными приращениями, и Мироздание ничего не знает о системах СИ и СГС, придуманных людьми, так как оперирует только количеством и закономерностями. Константа h обратно-пропорционально связана со скоростью света и отражает лишь разницу в виде коэффициента пропорциональности. Таким образом, по нашей теории получается, что частота и скорость связаны как противоположности через скорость света. Отсюда формулу (29) можно переписать в виде:
(31)
Для общего случая замкнутости между противоположностями, с учётом уравнения (26) при v2=c-v1, получим:
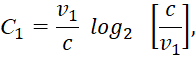(32)
Приняв 
, имеем:
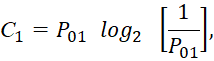(33)
Иными словами, этот полученный результат соответствует результату, полученному нами выше по формуле (28) и формуле Шеннона. Таким образом, формула пропускной способности в статистической радиотехнике вытекает как частный случай из формулы (5) при учёте только одной величины со значением P01.
Так как максимальная скорость изменения равна скорости света, то и максимальная мера изменений ‒ количество информации (это определение академика В. М. Глушкова) ‒ не может превышать этого значения. Изменение информации связано с носителями этой информации, то есть объектами Мироздания. Ещё раз отметим, что отсутствие носителей информации означает ноль информации. Не существует способа получения информации, если нет объектов её выражения. В соответствии с нашей теорией, объекты Мироздания выражаются через пространственно-временное искривление как в одной, так и в другой противоположности, с той лишь разницей, что кинетическая энергия в одной противоположности выражается через потенциальную энергию в другой противоположности. Соответственно мера количественных изменений по формуле (26) представлена через относительные значения скоростей объектов, а это связано напрямую с пространственно-временным искривлением (неоднородностью) по СТО и ОТО Эйнштейна.
Значения физических величин ограничены скоростью света и постоянной Планка. Причём с целью исключения полной независимости объектов друг от друга (а это бы означало, что они друг для друга не существуют) по нашей теории сh=1. Общее количество состояний с/h=Nм, и это число связано с постоянной Ридберга, что мы показали в [12, с. 5-26]. Отсюда, полученное соответствие формул для информации и энтропии доказывает, что представление в двоичной системе о бесконечности информации является неверным. Понятно, что ныне принятая нормировка по системе СИ или СГС не соответствует нашей трактовке, но не будем забывать, что Мироздание ничего «не знает» о выдуманных людьми системах. О парадоксах, получаемых из опоры на эти системы измерения, мы писали ранее в [15, с. 54-61]. Один из них ‒ это получение радиуса Шварцшильда с нарушением принципа термодинамического равновесия и получением «чёрных дыр». Таким образом, максимальное количество информации, как меры изменения при обмене между противоположностями, определяется максимальной скоростью обмена (или нормированной на неё величиной) по замкнутому циклу, и оно связано со значением скорости света.
Ещё раз напомним, что попытки связать энтропию с физикой процессов были сделаны до нас также в термодинамике, где рассматривается частный случай понятия энтропии [16, с. 332]. Она определяется из условия, что вероятность макросостояния пропорциональна его статистическому весу Ω, то есть числу микроскопических способов, которым может быть осуществлено данное макросостояние. Поэтому в качестве характеристики вероятности состояния можно было бы взять само это число, то есть Ω. Однако такая характеристика не обладала бы свойством аддитивной величины. Чтобы убедится в этом, достаточно разбить данную систему на две практически не взаимодействующие подсистемы. Пусть эти подсистемы находятся в состояниях со статическими весами Ω1 и Ω2. Число способов, которым может осуществиться соответствующее состояние системы, равно произведению чисел способов, которыми могут быть осуществлены состояниями каждой из подсистем в отдельности, то есть:
Ω=Ω1Ω2, (34)
Отсюда следует, что Ω не является аддитивной величиной. Взяв логарифм от соотношения (34), получим:
lnΩ=lnΩ1+lnΩ2, (35)
Из (35) получаем, что ln(Ω) ‒ аддитивная величина, и эта величина вычисляется так же, как и информация по формуле (4). При этом видим аналогию представления с (5) и имеем обоснование наличия суммы членов. Далее, в качестве характеристики вероятности состояния принимается величина S, пропорциональная логарифму статического веса. Формула для энтропии в этом случае выглядит в следующем виде:
S=klnΩ, (36)
Здесь k ‒ постоянная Больцмана; она является коэффициентом пропорциональности, который обеспечивает равенство:
dS=dq/T, (37)
где dS ‒ приращение энтропии при сообщении системе извне количества тепла dq при температуре системы T. В этом случае считается, что коэффициент пропорциональности в (37) равен единице. Впервые понятие энтропии было введено Клаузиусом в 1865 г. как функции термодинамического состояния системы. Эта функция имеет вид S = q/T (q – теплота, T ‒ температура). Классики не связывали энтропию в одной противоположности с информацией в другой противоположности. Анализ этой функции показал, что физический смысл энтропии проявляется, как часть внутренней энергии системы, которая не может быть превращена в работу. Иными словами, невозможно получить стопроцентное преобразование энергии в одной противоположности из-за влияния другой противоположности. Клаузиус эмпирически получил эту функцию, экспериментируя с газами. Л. Больцман (1872) методами статистической физики вывел теоретическое выражение энтропии по (36). Энтропия Больцманом была выведена для идеального газа и трактуется как мера беспорядка, то есть мера хаоса системы. Для идеального газа энтропии Больцмана и Клаузиуса тождественны, поэтому и эмпирическая функция Клаузиуса стала объясняться как мера вероятности состояния молекулярной системы. Формула Больцмана стала настолько знаменитой, что начертана в качестве эпитафии на его могиле.
Если представить постоянную Больцмана (k) неким безразмерным коэффициентом пропорциональности, то формула (36) является частным случаем формулы (33) потому, что в ней число возможных событий определяется в виде:
(38)
А это означает, что молекулы газа, обеспечивают одинаковую вероятность событий, которая и определяется постоянной Больцмана. Мы видим, что отличие от формулы двоичного исчисления (4) только в основании числа, от которого берётся степень. При этом формулу (37) с учётом того, что тепловая энергия вычисляется по формуле:
q=kT, (39)
можно представить как:
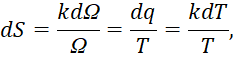(40)
Отсюда при интегрировании и равенстве констант интегрирования (иное означает чудо возникновения из ничего) получим, что:
Ω=T (41)
Отсюда вероятность состояния определяется физическим параметром, который характеризует температуру, и мы имеем формулу:
S=k lnТ, (42)
Так как температура напрямую связана с импульсом, то отсюда следует, что и полученные нами зависимости для импульса должны соблюдаться и для температуры. Если постоянную Больцмана (k) в (36) убрать в силу того, что она связана с системой измерения, придуманной людьми, что приводит к парадоксам с наличием «чёрных дыр», то получим:
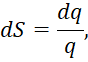(43)
В этом случае:
Ω=q, (44)
Так как сами молекулы в статическом состоянии покоя не имеют отличий, и не несут никакой информации в силу полной идентичности, то отличие определяется воздействием, связанным с их энергией, что и даёт энтропию в замкнутом объёме. Любые изменения всегда связаны с движением. Поэтому статическое расположение молекул в состоянии покоя не может дать ни понятие информации, ни понятия энтропии. Всё определяется динамикой изменения процессов в противоположностях. Соответственно, мы видим, что отличие вычисления энтропии по Больцману отличается от вычисления информации только тем, что при вычислении информации вместо постоянной Больцмана (k) и величины Т, необходимо ввести значения k=T* и Т*=1/Т. Одновременно мы видим, что при замене значения Ω на T в формуле (42), имеем бесконечное возрастание энтропии при бесконечном возрастании температуры, ‒ а это соответствует наличию «ультрафиолетовой катастрофы». Но температура напрямую связана со скоростью движения молекул. При этом известно, что скорость частиц ограничивается скоростью света с в соответствии с СТО и ОТО Эйнштейна, и поэтому температура не может возрастать до бесконечности. Таким образом, чтобы связать энтропию и информацию как противоположных величин и для исключения парадоксов, формулу Больцмана (36) нужно скорректировать с учётом реальных физических процессов, обратно пропорциональной связи между противоположностями, закона сохранения количества и связи скорости частиц с температурой или тепловой энергией. Этот шаг можно сделать исходя из равенства:
(45)
Фактически формула (45) характеризует эквивалент связи частоты электромагнитной кинетической энергии с температурой. При этом скорость v, здесь определяет пространственно-временное искривление по СТО и ОТО Эйнштейна, связанное с потенциальной энергией. Однако, так как кинетическая и потенциальная энергия в противоположностях меняются местами, то учитывая, что по нашей теории сh=cm0=1, а частота волн Луи де Бройля по формуле (30) fдб=сvдб, то мы можем получить прямую связь температуры и скорости в виде:
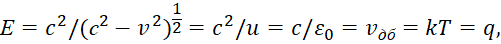(46)
Понятно, что, так как наличие постоянной Больцмана (k) связано с выбором системы измерения, придуманной людьми, то можно получить полное соответствие между скоростью vдб и температурой T при использовании нормировки. Однако значение температуры даже, исходя из распределения по частоте (скорости движения) при непрерывных (а не дискретных) значениях, даёт наличие «ультрафиолетовой катастрофы». Чтобы избежать «ультрафиолетовой катастрофы» в 1900 г. Планк предположил, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых пропорциональна частоте излучения E=ℏω. Далее Планк предположил, что если излучение испускается порциями, то его энергия Еn должна быть кратной этой величине E=nℏω, (n=0, 1, 2, ...).
Однако теория излучения квантами противоречит классической электродинамике, так как электрон, вращаясь вокруг протона должен непрерывно излучать в силу ускоренного движения. Как в этом случае квантовать порции электромагнитного излучения во времени? Чтобы не было излучения в некоторые моменты времени (что даёт порции электромагнитного излучения) надо иметь дискретность в формировании пространства и времени и соответственно процесс обмена не должен быть моментальным и должен иметь ограничение в скорость света, что показано в нашей теории. То есть пространство и время – это тоже объекты в мироздании, и они не могут быть представлены иначе, чем через дискретность (различие), что и даёт необходимость квантования. Не сумев решить проблему восполнения энергии при таком излучении (при отсутствии механизма восполнения энергии электрон бы неминуемо упал бы на протон), а также, не поняв роль констант мироздания, Бор исключил законы электродинамики по излучению на дискретных орбитах. И это привело к вероятностному подходу в квантовой механике с механизмом телепортации. В [17, с. 16-34] мы показали, каким образом осуществляется восполнение энергии без нарушения законов классической электродинамики за счёт силы Кулона и силы Лоренца с учётом констант электрической (ε0) и магнитной (μ0) проницаемости. Это стало возможным благодаря тому, что существует общий пространственно-временной и электромагнитный континуум, что связано с взаимным преобразованием между двумя глобальными противоположностями при замкнутой системе исходя из [3, с. 32-58]. При этом понятно, что явление дискретизации с постоянной Планка связано с исключением однородности. Именно это и даёт дискретные орбиты с излучением в виде квантов с переходом с одной орбиты на другую. Отметим, что Планк использовал закон Больцмана [18, с. 323; 19, с. 29] в виде распределения энергии частиц по вероятностным состояниям, так как энергия электромагнитного поля поглощается частицами, и если нет электромагнитной энергии для поглощения, то и нет частиц с данной энергией:
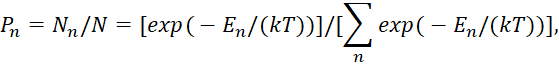(47)
Этот вероятностный закон распределения соответствует замкнутой системе, что потом будет видно по формуле (49). И как мы показали в [12] случайный процесс при замкнутой системе связан только с наличием действия и противодействия глобальных противоположностей друг на друга при соблюдении закона сохранения количества. Отметим, что вероятность здесь понимается чисто гипотетически, так как в формуле (47) присутствуют конкретные значения энергии и закон распределения также однозначен, а значит, вероятности должны отсутствовать. Если учесть формулу (45), то значения Е и kT имеют обратно пропорциональную связь, то есть выступают как противоположности, откуда можем записать:
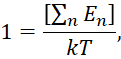(48)
Иными словами, у нас распределение энергии по частотам не может быть произвольным, а зависит от значения энергии в противоположности. Как мы уже показали ранее, формула обратно пропорциональной связи соответствует формуле связи энтропии и информации (9). В этом случае, если энергию одной противоположности рассматриваем как энтропию, то энергия другой противоположности связывается с наличием информации.
Далее учтём, что сумма в знаменателе формулы (47) представляет собой сумму членов бесконечной геометрической прогрессии с первым членом равным единице, и знаменателем прогрессии равным exp(-x), где x=ℏω/(kT). Соответственно получаем:
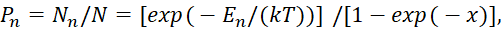(49)
Иными словами, вклад по частотам, а значит и по скоростям не равноценен. Тогда справедлива запись вида:
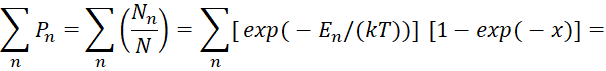
(50)
Это означает, что количество состояний системы мироздания ограничено и может быть нормировано к единице. Отсюда можно найти среднее значение энергии, с соответствующей частотой по формуле:
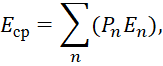(51)
В итоге, с учётом [20, с. 216], можно получить формулу для средней энергии излучения в виде:
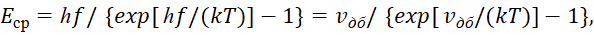(52)
Исходя из формулы (52) следует, что при динамике взаимодействия противоположностей, энергия энтропии, которая связана с температурой, не может возрастать до бесконечности в силу наличия минимального дискретного элемента в виде постоянной Планка. Более того, в системе мироздания существует равновесное состояние между замкнутыми друг на друга противоположностями, которое определяется максимумом энергетического спектра [19, с. 29] и на основании чего с учётом констант электрической и магнитной проницаемости мы вычислили значения отношения массы протона к массе электрона [13, с. 12-32]. Отсюда для получения однозначности к вычислению, как энтропии, так и информации, с учётом того, что для исключения парадоксов температура не может иметь ни непрерывных значений, ни неограниченного роста при сопоставлении с (32) и при соответствующей нормировке, нужно использовать общую формулу для энтропии вида:
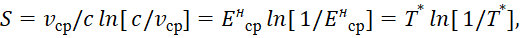(53)
Здесь значение vср является величиной обратно пропорциональной к величине температуры (Т) как значение vдб в формуле (52). При этом значение энтропии зависит от значения энергии, которая при учёте нашей теории становится безразмерной величиной. Соответственно исключается парадокс бесконечного роста энтропии, так как предел скорости ограничен значением в скорость света. Единообразие функции представления информации и энтропии с разницей на константу говорит о том, что разумные (а они всегда представляются разумными с точки зрения того, кто их осуществляет) направленные действия в одной противоположности рассматриваются как вносимый беспорядок в другой противоположности. Подчеркнём, что не воздействовать через закономерности противоположности друг на друга не могут, так как иначе они бы вообще не имели бы связи между собой и таких характеристик как количество и качество в соответствии с формулами (2). Термодинамическое равновесие по формуле Планка определяет равновесное состояние противоположностей при обмене за счёт распада и синтеза, и это означает, что существует оптимум между информацией и энтропией, что исключает наличие информации без энтропии, и наоборот.
Однако, как мы отмечали выше, в замкнутой системе между противоположностями в мироздании, если исходить из наличия воздействия только от одной противоположности с присутствием заданной закономерности возникает вопрос о детерминированности (фатальности) всех происходящих событий. Действительно, в физических законах нет неоднозначности, и всегда воздействие даёт противодействие. Тогда откуда берётся возможность выбора у живых существ?
Чтобы понять это, необходимо вспомнить всю последовательность формирования законов мироздания из логики.
Здесь, как показано выше, закон сохранения количества подразумевает симметрию процессов в противоположностях, где сложение в одной противоположности выглядит как вычитание в другой противоположности, и наоборот. Отсюда также следует, что скорость света и постоянная Планка в противоположностях также меняются местами, и мы имеем обратно-пропорциональную связь между противоположностями, то есть с = 1/h. Собственно необходимость смены представления связана и с тем, что отсутствие разницы представления объектов в противоположностях означает, что отличий между противоположностями нет. Обратно-пропорциональная связь между противоположностями с различным представлением в них объекта обуславливает и иерархическое построение противоположностей в Мироздании, что исключает замкнутость объектов на одном уровне иерархии с образованием вечного двигателя помимо самого Мироздания. Одновременно, так как минимальная величина в одной противоположности благодаря обратно-пропорциональной связи является максимальной в другой противоположности, обеспечивается возможность усиления воздействия (влияния). В противном случае сохранение представления объекта в виде минимальной величины в обеих противоположностях исключало бы воздействие минимальных объектов на максимальные объекты, и усиление было бы невозможно. Далее следует, что закон сохранения количества со сменой сложения на вычитание в противоположностях подразумевает квадратичную форму записи, так как равенство вида (1) можно получить только в случае нулевых значений, а это отсутствие Мироздания; отсюда необходима запись в виде (2).
Доказательство необходимости такого подхода подробно описано нами в [2, с. 42-61]. Из формулы (2) также следует, что невозможно отделить наличие любого объекта, выраженного количественно без соответствия некоторой закономерности. И это как раз и определяет связь количества с качеством. Однако, повторим, что если количество определяет наличие объекта как единого целого при условии отсутствия распада, то закономерность невозможно рассматривать без воздействий, так как иное означало бы полную замкнутость. Если рассматривать объект как неживое существо, то его влияние имеет строго определённую зависимость, которая определяется средой, окружающей этот объект, что и выражено в физических законах. При этом живое существо обладает степенью свободы в выборе закономерности своего влияния. Иными словами, окружающая среда для данного объекта даёт возможность в выборе. Но как это происходит с точки зрения законов мироздания при наличии однозначных физических законов?
Здесь мы должны отметить, что математически это следует из формулы (2), где квадратичная форма для объекта выполняется при движении по возможным двум направлениям exp(ix) и exp(‒ix) в одной противоположности, в другой противоположности выбранному направлению будет соответствовать процесс либо синтеза exp(w), либо распада exp(‒w). Физически это связано с преобразованием при движении длины по любой координате вовремя, и наоборот по СТО и ОТО Эйнштейна. Это даёт неопределённость, так как важно само движение с преобразованием вовремя, и не важно, по какой координате. Надо отметить, что с неоднозначностью в выборе решения столкнулся ещё Дирак [21], так как в релятивистской теории, энергия свободной частицы связана с её импульсом и массой покоя соотношением, допускающим два равноправных решения (неоднозначность):
(54)
Поэтому при «линеаризации» в виде системы уравнений Дирака [3, с. 32-58]:
| (Е-m0c2)Ψ1-c(Px-iPy)Ψ4-cPzΨ3=0, (Е-m0c2)Ψ2-c(Px+iPy)Ψ3+cPzΨ4=0, (Е+m0c2)Ψ3-c(Px-iPy)Ψ2-cPzΨ1=0, (Е+m0c2)Ψ4-c(Px+iPy)Ψ1+cPzΨ2=0. | (55) |
значение количества энергии может быть как положительное, так и отрицательное.
Понятно, что в нашей теории это связано не с отрицательной и положительной энергией, а с процессом в динамике взаимодействия с поглощением и излучением, так как в системе уравнений Дирака исходными для взаимодействия являются волновые функции Ψ:
Ψ(t,r)=exp[-i(Ett-Pxx-Pyy-Ezz)]=exp[-i(Еt-Рr)], (56)
связанные с процессом излучения и поглощения в дифференциальной системе уравнений Дирака вида:
(iћ + (iћ ћ ) + iћ =0,(iћ  + (iћ ћ ) - iћ =0,(iћ  + (iћ ћ ) + iћ =0,(iћ  + (iћ ћ ) - iћ =0. | (57) |
Отсюда значение Е представляет величину количественных изменений во времени (как положительных, так и отрицательных) для обеспечения закона сохранения количества в одном случае выбора при распаде, а в другом случае при синтезе.
Понятно, что выполнение нижнего уравнения (2) с возможностью выбора воздействия каждой из противоположностей возможно только при наличии обратно-пропорциональной связи между ними, где максимальная величина в одной противоположности будет минимальной величиной в другой противоположности. Это связано с тем, что в противном случае воздействовать для изменения друг друга противоположности не смогут, так как для управления необходимо неравенство в представлении, иначе, градиента изменения, то есть неоднородности, просто не будет. Отсюда имеем в формуле (2) правило для аргументов:
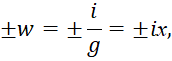(58)
Тогда линейно изменяющиеся процессы в аргументе функций в одной противоположности будут нелинейными в другой противоположности. Это означает, что отсутствие силового воздействия в одной противоположности однозначно даёт её присутствие в другой противоположности. Кроме того, аргументы функций также являются корпускулярно-волновыми объектами, принадлежащими Мирозданию, так как ни один объект Мироздания не может принадлежать только одной противоположности (иначе он замкнут сам на себя, и его невозможно обнаружить, и это ноль, который ни с чем не взаимодействует). Отсюда скалярному представлению в одной противоположности в виде единой величины соответствует векторное представление в другой противоположности в виде двух противоположных величин, что обеспечивается за счёт мнимой единицы (атрибута принадлежности с учётом противодействия), как это видно по формуле (2). По сути, это означает невозможность отображения в одном и том же виде объекта в противоположностях без различий. Следовательно, мы вынуждены представить значения аргументов в (58) в виде:
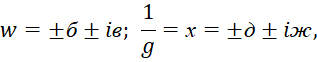(59)
На основе геометрических преобразований и формул Эйлера (именно на основе их получается общая формула мироздания, которой подчиняются все объекты) и с учётом ch(в) = cos(iв), ish(в) = sin(iв), например, получаем уравнения вида:
| (60) |
Это соответствует функции Луи де Бройля и функциям в (2), характеризующим объекты мироздания в замкнутом цикле обмена. Собственно, иное представление объектов означало бы их независимость от замкнутой системы мироздания, и отсюда, был бы разрыв с наличием чудес. При этом начальный объект в виде единого целого и характеризующийся в одной противоположности аргументом w, в противоположности не представляется единым целым и разбивается на противоположности б+iв (при этом амплитудные значения новых объектов также изменяются в соответствии со значениями гиперболических синусов и косинусов), иначе одинаковое представление вообще исключает наличие любых противоположностей. Отсюда следует, что в соответствии с иерархическим построением Мироздания, по которому каждый объект Мироздания обязан разбиваться на противоположности для взаимодействия, значения б и в, д и ж также можно разбить на противоположности с соответствующими геометрическими преобразованиями и т. д. Таким образом, с учётом иерархии Мироздания, обратно пропорциональной связи между противоположностями, и свободой выбора за счёт квадратичного равенства, процессы внутри Мироздания имеют многообразие и свободу выбора в рамках соблюдения закона сохранения количества. Собственно, и принцип Гюйгенса-Френеля с огибанием волной препятствия также не был бы возможен, так как противодействие выполнялось бы по направлению действия из-за отсутствия выбора. Именно поэтому сила Кулона имеет противодействие в виде силы Лоренца по ортогональному направлению, и они переходят друг в друга при смене системы наблюдения из противоположностей.
Таким образом, сама суть наличия выбора у живых существ связана с тем, что каждая из противоположностей обладает количеством в виде объектов (зависимая составляющая, на что оказывается влияние) и качеством (независимая составляющая закономерность). Если предположить, что существует только детерминированный закон между противоположностями (однозначная связь), то тогда следует исключить наличие влияния в виде закономерности одной из противоположностей, а это есть исключение и самих противоположностей, то есть, нет противодействия в силу того, что все процессы определяются одной общей закономерностью в аргументе. И этот аргумент не имеет зависимой части, то есть принадлежит одной противоположности, но тогда возможны чудеса. То есть, это означает, что аргумент как объект не принадлежит замкнутой системе Мироздания и может быть любой закономерностью и здесь не может быть физических законов, что не наблюдается. Для исключения парадокса исключения физических законов аргументы в формулах (2), слева и справа от знака равенства, также должны иметь зависимые и независимые составляющие, что даёт свободу выбора с учётом неоднозначности квадратичной формы (2). Отсюда вывод, что, все объекты входят в Мироздание и своими корпускулярно-волновыми частями принадлежат противоположностям, они не могут представляться иначе помимо зависимых и независимых составляющих в Мироздании и соответственно разница между живыми и неживыми существами определяется степенью свободы выбора, так как любой объект имеет характеристику в виде количества и качества.
Отсюда общий вывод, что наличие живых существ ‒ это результат наличия глобальных противоположностей, которые за счёт закономерностей (это качество) осуществляют воздействие на количество от противоположности.
Иными словами, глобальные противоположности выступают по отношению друг к другу зависимыми и независимыми частями, и отсутствие такой интерпретации вообще исключает необходимость самих противоположностей.
Понятно, что условия множественности выбора меняются для объектов в зависимости от места, занимаемого в иерархии Мироздания при обратно-пропорциональной связи между противоположностями. Здесь действие (влияние) одной противоположности разрушаются действиями другой противоположности, то есть информация (закономерность) в одной противоположности означает энтропию (хаос, шум) в другой противоположности и здесь также имеет место равновесное состояние, так как иное противоречит замкнутости Мироздания и представления такого представления в виде константы.
Каким образом это происходит, мы показали выше через связь физики и кибернетики. С учётом того, что количество возможных объектов, а, следовательно, и уровней иерархии в каждой из противоположностей ограничено из-за величины Nм, то суть развития по спирали или деградации каждого объекта определяется его действиями. То есть живое существо, как один из Nм объектов мироздания, само определяет занимаемую закономерность, благодаря своим действиям и желаниям. Иное исключает наличие независимой составляющей у живых объектов и противоречит возможности выбора, а значит и наличию противоположностей в нём как корпускулярно-волнового объекта. Если учесть практическую часть теории Дарвина, то мы видим отличия видов существ, и самым развитым из этих видов в этом мире является человек. Однако мы видим скачкообразное изменение видов, а это противоречит теории Жан Батиста де Ламарка, который считал, что вновь приобретаемые признаки с изменением вида формируются ещё при жизни за счёт влияния «живой силы». Теория Жан Батиста де Ламарка требует не скачкообразного изменения видов, а их плавного перехода от одного вида к другому, что не наблюдается. При этом влияние на генный аппарат должно быть сделано при жизни с передачей потомству. Одновременно теория Дарвина с учётом влияния случайных процессов на генный аппарат видов также имеет парадоксы. Случайный процесс привёл бы к распаду генного аппарата раньше, чем смогла бы возникнуть необходимая лучшая мутация. Наличие многообразия видов отрицает случайный характер путём мутации генного аппарата. Таким образом, остаётся один единственный вариант, когда наши действия в одной противоположности формируют корпускулярные изменения в другой противоположности. Иными словами, скачкообразные процессы по качеству в каждой из противоположностей формируются действиями из другой противоположности и связаны с иерархией в мироздании. Собственно, именно на этом основана связь корпускулярных свойств одной противоположности за счёт обмена через волновые свойства от другой противоположности. Отсюда «наше я» само формирует своё место в противоположности в системе эволюции видов за счёт своих действий, что нами интерпретируется как судьба. Подтверждение такого подхода с фатальностью событий в нашей теории мы видим из того, что закономерность изменений в одной противоположности, на основе закономерности в другой противоположности, вытекает из известного опыта с дифракционной картиной. Действительно, дифракционная картина по рисунку 3 при двух щелях была бы невозможна, если допустить, вариант случайного прохождения электронов через эти две щели и был бы вариант пиков напротив каждой из щелей как при одной щели.
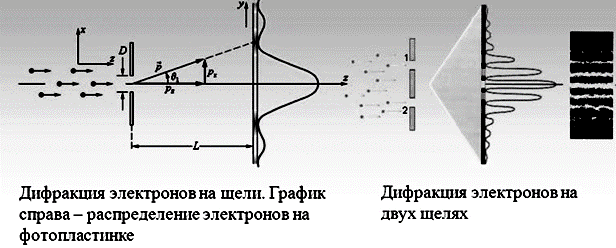
Рис. 3. Дифракция электронов на щелях
Чтобы исключить воздействие электронов друг на друга, советские физики Л. М. Биберман, Н. Г. Сушкин и В. А. Фабрикант осуществили в 1949 г. опыт, в котором интенсивность электронного пучка была настолько слабой, что электроны проходили через прибор заведомо поодиночке. Промежуток времени между двумя прохождениями электронов через кристалл примерно в 30000 раз превосходил время, затрачиваемое электроном на прохождение всего прибора. При достаточной экспозиции была получена дифракционная картина, ничем не отличающаяся от той, какая наблюдается при обычной интенсивности пучка. При этом получаем интерференционную картину, соответствующую закономерности, связанной с волной Луи де Бройля. Так как исключена зависимость, связанная с взаимным влиянием электронов друг на друга, а траектория электрона всегда строго определена со вспышкой только в одном месте, то возникает вопрос: «Каким образом последующий электрон, после вспышки на экране предыдущего электрона, определяет место своей вспышки для получения общей интерференционной картины по волновой закономерности Луи де Бройля?» Это возможно только в случае, если существует общая закономерность влияния на электроны, которая определяет общее распределение электронов и зависит не от времени, а от выбора предыдущими электронами положений вспышек на экране. То есть, действия предыдущих электронов сформировали в противоположности корпускулярный вид, который уже в нашей противоположности представляет закономерность, которая и определяет соответствующее положение на экране последующих электронов. Иными словами, сформированные закономерности наших желаний в одной противоположности (а это связано с нашими действиями), дают корпускулярное представление в другой противоположности. По рисунку 3 это отражено в виде дифракционной картины справа.
Отсюда, так как ни один из Nм – объектов Мироздания не может исчезнуть (не будет соблюдаться закон сохранения количества), то следует предположить, что наше «я» как объект Мироздания при смерти переходит в противоположность, но на тот уровень иерархии, который мы себе обеспечиваем своими действиями при жизни. Иными словами, формируемые нами закономерности определяют наш будущий вид как в дифракционной картинке за всё время нашей жизни (отпущенного времени). Одновременно, повторим, что, если бы происходило исчезновение нашего «я», то это означало, что мы как объект возникли из нуля, что противоречит законам физики. Кроме того, если предположить вечное существование нашего «я» в одной противоположности без перехода в другую противоположность, то это означает, что оно является не объектом внутри мироздания, а самим мирозданием и соответственно в этом случае должно быть константой без изменений, чего также не наблюдается. Одновременно, так как в Мироздании для сохранения количества соблюдается закон противодействия на действие (иначе были бы возможны чудеса) с разнесением во времени (по крайней мере, на скорость света), то это означает, что сотворил, то и получишь, не в этой, так в следующей жизни в противоположности. Собственно отсутствие противодействия вновь нас возвращает к варианту наличия одной противоположности, а значит к чудесам.
Поясним, что при переходе в противоположность наше «я» не попадает на тот же уровень, а либо поднимается вверх по иерархии, или опускается вниз по иерархии, что даёт скачок. Это мы показали в [12, с. 5-26]. И связано с это тем, что иначе был бы возможен вечный двигатель, то есть замкнутость на одном уровне иерархии без необходимости других уровней. Принцип обитания нашего «я» в теле довольно сложен, так как мы представляем собой целую системную иерархию живых существ, воздействие на которые осуществляется благодаря обратно-пропорциональной связи, что даёт усиление. И как показывает практика, чтобы жить, надо преодолевать свою лень, как в физическом, так и умственном плане, то есть самим воздействовать и формировать закономерности. Иными словами, наше «я» представляет собой волновое отражение в виде воздействий (закономерностей) в одной противоположности, что в другой противоположности переходит в некий корпускулярный вид [3, с. 32-58]. Отсюда события, которые происходят с изменением нашего организма в корпускулярном виде, сказываются на возможности волнового воздействия, и в противоположности влияют на корпускулярный вид нашего «я». В совокупности с нашим воздействием это приводит к новому формированию нас как вида. Понятно, что здесь мы представили весьма упрощённое понимание исходя из невозможности исчезновения объектов из Мироздания.
При этом, благодаря сформированным новым законам философии на основе логики при отсутствии чудес в Мироздании, мы смогли обосновать необходимость свободы выбора с наличием живых существ и закона сохранения количества, чего диалектический материализм дать не смог.
Таким образом, наша теория позволяет объяснить не только многие парадоксы в физике и показать их решение, но и впервые смогла представить формирование живых существ на основе взаимодействия противоположностей, обосновала и вывела законы их существования.
Выводы:
- Нам удалось объединить понятия энтропии и информации на основании законов физики и привести их к единому виду. Это связано с тем, что направленные действия в одной противоположности характеризуются изменениями (а это и даёт информацию). Одновременно в другой противоположности это изменение рассматривается как случайный процесс (энтропия). Так как изменения протекают в замкнутой системе на две глобальные противоположности и есть ограничения в скорости изменения (скорость света) и по величине минимального объекта (постоянная Планка), то мы имеем ограничения в количестве информации и значению энтропии. И это потребовало усовершенствования формулы Больцмана (42) с учётом замкнутости мироздания и разницы представления процессов в противоположностях.
- Законы возникновения живых существ определяются:
- наличием корпускулярно-волнового дуализма с представлением электромагнитных составляющих в одной противоположности в виде пространственно-временного искривления в другой противоположности. В этом случае кинетическая энергия направленного движения в одной противоположности имеет вид потенциальной энергии в другой противоположности. Это определяет представление массы в одной противоположности как скорости в другой противоположности, и, наоборот, с выполнением закона по формуле аналогичной формуле (18), но с учётом взаимодействия между противоположностями;
- условием взаимодействия глобальных противоположностей через обмен, которые не могут не вносить изменения друг в друга, иначе они будут независимы, и являться друг для друга нулём;
- способностью воздействовать на основе обратно пропорциональной связи между противоположностями благодаря тому, что максимальное значение в одной противоположности является минимальным в другой противоположности, и это позволяет выстроить иерархию в управлении с усилением воздействия и обосновывает само иерархичное построение Мироздания. Кроме того, обратно-пропорциональная связь между противоположностями определяет необходимость такой же связи между массой и скоростью по формуле (23), что даёт возможность физического представления информации и энтропии с абстрактным представлением по Шеннону. Необходимо отметить, что наличие формулы (23) следует и из представления формулы энергии Эйнштейна как замкнутой системы подчиняющейся уравнению окружности, что было нами показано в [10, с. 41-53];
- иерархией построения Мироздания, когда любой объект Мироздания, отражающий единое целое в одной противоположности, в другой противоположности делится на противоположные части и т. д. В противном случае он будет принадлежать одной из противоположностей, а значит, не участвует во взаимодействиях, и тогда в мироздании его обнаружить невозможно;
- свободой выбора направления воздействия (плюс или минус), что связано с квадратичной формой связи противоположностей по формуле (2) с условием закона сохранения количества (аналогия по формуле Эйнштейна (54)). При этом векторное значение с проекциями по координатам длины переходят в одну общую проекцию по времени, которая является скалярной величиной в соответствии с СТО и ОТО Эйнштейна. Соответственно, в результате двустороннего обмена между противоположностями, скалярная величина даёт в противоположности вектор независимый по направлению, но соответствующий по количеству;
- соответствием каждому количеству соответствующего качества (закономерности), что требуется для выполнения замкнутости мироздания по формуле (2). Иными словами, закон диалектического материализма с переходом количества в новое качество приобретает математическое воплощение по формуле (2);
- наличием замкнутой системы между противоположностями и существованием максимальной скорости взаимодействия (скорость света) и минимального значения величины объекта (постоянная Планка). Это позволяет решить задачу совершенствования (или деградации) живых существ, за счёт перехода в противоположность со сменой уровня иерархии. Смена уровня иерархии и даёт скачкообразные изменения от вида к виду. Причём, желания и действия в одной противоположности формируют соответствующее корпускулярное представление в другой противоположности, в зависимости от содеянного. Это связано и с тем, что время в одной противоположности переходит в длину в другой противоположности. Иное исключало бы возможность противодействия на действие, так как не было бы сохранения (информации) на что надо получить противодействие. Экспериментально это подтверждается дифракционной картиной по рисунку 3;
- отсутствием бесконечной энтропии (разрушения) каждой из противоположностей, так как это бы означало полное управление одной противоположностью другой, при отсутствии обратного воздействия, а значит изменения. Именно этот недостаток был положен в формулу Больцмана (42) и распространён на теорию Дарвина со случайным возникновением живых существ;
- решением проблемы скачкообразного перехода от вида к виду эволюционным путём за счёт обмена между противоположностями, с формированием новой корпускулярной основы в противоположности на основе действий и желаний от электромагнитного исполнения в первоначальной противоположности. В этом случае переход в противоположность при формировании корпускулярного представления (в виде потенциальной энергии) за счёт направленных действий от другой противоположности (кинетическая энергия), даёт иерархию построения генного аппарата в этой противоположности.
Причём скачкообразное изменение говорит о том, что свобода выбора ограничивается воздействием от другой противоположности, то есть в формировании генного аппарата участвуют обе противоположности, а не одна из них. Иными словами, существует причинно-следственная связь, по которой предыдущие события влияют на последующий выбор. Поэтому попытки построить робота (систему кибернетического управления) подобного живому существу обречены на провал. Для этого надо пройти всю цепочку эволюции ‒ причины возникновения данного вида.
Таким образом, при доказательстве необходимости возникновения живых существ мы использовали уже известные законы философии, физики, математики и кибернетики, но с учётом дополнений из теории мироздания, которые позволяют исправить ошибки и парадоксы, которые не позволяли связать все законы в единое целое и понять необходимость присутствия живых существ в мироздании.
.png&w=640&q=75)
