В публикациях [1, с. 12-32; 2, с. 5-26] мы подробно показали, какие подгонки под результат были допущены при определении первой боровской орбиты по теории Бора и при вычислении спектра водородоподобного атома. Главной ошибкой Бора был отказ от излучения электронов при движении на дискретных орбитах вокруг протона, что противоречило законам электродинамики. Именно отсутствие излучения, как и поглощения, электромагнитной энергии атомом означает его полную замкнутость на себя, и в этом случае его обнаружить в нашем Мироздании невозможно. Кроме того, в этом случае должна наблюдаться полная нейтральность атома, так как любая разность потенциалов между ядром и электронами означает наличие сил притяжения и отталкивания, а это связано с ускорениями, дающими излучение и поглощение, что опять противоречит отсутствию излучения и поглощения на дискретных орбитах. Чтобы уйти от наличия ускорений с исключением излучения, был предложен принцип неопределённости Гейзенберга с отсутствием определённости по значениям потенциальной и кинетической энергии. Иными словами, если нет определённости в значении энергий, то нет и ускорений. Это также послужило внедрению в квантовую механику туннельного эффекта прохождения через потенциальный барьер. Соответственно в [1, с. 12-32; 2, с. 5-26] мы выявили причину совпадения практических результатов с данными подгонками под результат.
Как уже отмечалось в [1, с. 12-32; 2, с. 5-26] данные подгонки являются результатом отсутствия понимания логики возникновения физических законов от простого состояния к сложному состоянию. Физический закон воспринимался в качестве постулата, и не рассматривалась причина его появления. Отсюда, чтобы получить совпадение теории с практикой стали использоваться способы «сшивания решений» с наличием неких постулатов. В классической электродинамике такой метод «сшивания решений» относится к рассмотрению процессов на границе раздела сред. Какие парадоксы при этом возникают и как они решаются мы описали в [2, с. 5-26]. Недостаток метода «сшивания решений» в том, что результат зависит от того, какие начальные условия (иной раз необоснованные) принимаются за основу, что и даёт подгонку под результат. Однако есть противоречия, которые невозможно решить на основе даже таких подгоночных подходов. Например, искривление прохождения света в так называемом гравитационном поле (результат представления пространства и времени через ОТО Эйнштейна) нельзя описать на основе принципа замедления движения света, так как это противоречит СТО Эйнштейна. Действительно, если бы свет имел замедление в так называемом гравитационном поле (среде распространения), то он повторял бы свойства частиц. Для корпускулярных частиц суть замедления связана с торможением. Однако свет при выходе из более плотной оптической среды продолжает движение со скоростью света, а частица ‒ нет. Это говорит о том, что замедление скорости света связано не с торможением, а со взаимодействием с элементами оптически плотной среды через поглощение и излучение, что и интерпретируется как торможение. Результатом подтверждения этого является принцип Гюйгенса-Френеля с наличием вторичных источников возбуждения в так называемом вакууме. Более того, интерференция света с учётом принципа суперпозиции приводила бы к исчезновению электромагнитного поля при сложении в противофазе, и дальнейшее распространение света было бы невозможно. Действительно, компенсация электромагнитных составляющих в противофазе даёт ноль, и если исключить преобразование электромагнитных составляющих в нечто иное (в нашем случае в составляющие пространства и времени), то распространения дальше в последующем не будет. Но этого не наблюдается, что также говорит о наличии взаимодействия света со средой с поглощением и излучением, отсюда и требование к наличию вторичных (сторонних или фиктивных) источников излучения по принципу Гюйгенса-Френеля. Иными словами, так называемое гравитационное поле представляет собой корпускулярно-волновой объект, который характеризуется корпускулярными свойствами через значения электрической (ε0) и магнитной (μ0) проницаемостей, а волновые электромагнитные свойства определяются вторичными источниками поглощения и излучения. Иными словами, мы имеем общий пространственно-временной и электромагнитный континуум, где любой объект Мироздания должен обладать электромагнитными и пространственно-временными свойствами. Взаимодействие через излучение и поглощение приводит к изменению направления движения света, а исчезновение электромагнитного поля и появление его вновь связано с преобразованием кинетической энергии в потенциальную энергию, и, наоборот (без преобразования нет и причин для изменений). Это говорит о том, что при решении задач необходимо учитывать принципы физического взаимодействия любого объекта со средой, что и было показано нами в [1, с. 12-32; 2, с. 5-26] с исключением парадоксов.
Как было отмечено выше, в квантовой механике к методу «сшивания решений» добавился и вероятностный подход. Здесь для обоснования запрета на излучение придумали движение электрона не по орбите, а в виде орбиталей (оболочек), получаемых вероятностным образом в виде волновых функций по принципу неопределённостей Гейзенберга (рис. 1).
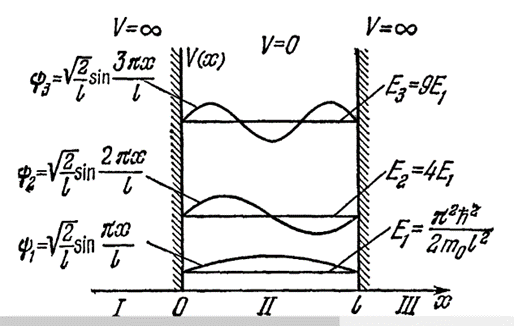
Рис. 1. Частица в потенциальной яме с бесконечно высокими стенками
Соответственно приводим ссылку из [3, с. 114]: «Хотя представление об орбитах, как и вообще представление о траекториях микрочастиц, является неправомерным, момент, обусловленный движением электронов в атоме, называют орбитальным». Читатель, с нормальным логическим мышлением, сразу обратит внимание на парадокс, при котором волновой вид определяется закономерностью детерминированного физического закона, а он явно противоречит вероятности, которая исключает любую закономерность, а значит и физический закон. В действительности вероятность ввели для того, чтобы убрать физический закон, связанный с излучением при детерминированном движении электрона по орбите вокруг протона, но представили при этом волновую функцию в качестве основы для вероятности, что говорит уже о наличии физического закона, а он требует интерпретации и связи с другими законами. При наличии закона любое волновое движение не может обойтись без изменения направления с наличием ускорений и замедлений в соответствии с наличием волнового вида (отсутствие детерминированной закономерности – это «белый шум»), а это опять должно давать излучение и поглощение. Иными словами, от чего ушли, к тому и пришли. Но, чтобы оправдать некоторые свойства типа холодной эмиссии, на основе вероятности, при «сшивании решений», придумали телепортацию через потенциальный барьер и назвали его туннельным эффектом [4, с. 89] (рис. 2).
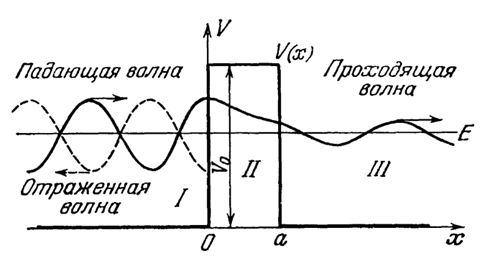
Рис. 2. Прохождение частицы сквозь потенциальный барьер прямоугольной формы
А это означает, что опровергли разом необходимость СТО Эйнштейна и необходимость наличия любых физических законов. При этом значение волновой функции должно иметь на границе раздела сред максимальное значение, что противоречит минимуму функции по рисунку 1, из которого также видно, что для волновых функций со значением с величиной Е1 и Е3 наибольшая вероятность будет в том самом месте, где должен находиться протон. При этом понятно, что с классической точки зрения туннельный эффект представляется абсурдным, так как частица «находящаяся в туннеле» должна была бы обладать отрицательной кинетической энергией (в туннеле Е<V). Однако этот парадокс не смутил учёных, они заявили, что туннельный эффект – явление специфически квантовое, не имеющее аналога в классической физике. Они посчитали, что в квантовой механике деление полной энергии на кинетическую энергию и потенциальную энергию не имеет смысла, так как противоречит даже принципу неопределённости Гейзенберга [5, с. 69]. То есть наличие таких чудес «узаконили» на основании соотношения неопределённостей Гейзенберга в силу неопределённости значения импульса, а значит и невозможности определить точные значения кинетической и потенциальной энергии. Иными словами, раз значение импульса определить точно невозможно, значит, и говорить о наличии излучения или поглощения невозможно, ‒ нет величин оценки. По сути дела, это есть отказ от необходимости разграничения на противоположности в каждом объекте Мироздания. Далее обман с подгонкой под результат в физике и квантовой механике идёт по возрастающему процессу, так как отсутствие закономерностей означает наличие любых чудес.
Однако многие учёные утверждают, что благодаря такому подходу удалось получить совпадение теоретических результатов с практическими результатами, и мол, поэтому это подтверждает «истину» таких введений вероятности в законы физики. То есть было как бы теоретически и практически доказано, что классический подход в физике исключает наличие совпадения результатов практики и теории аж на два порядка. Поэтому нам необходимо раскрыть, каким образом получались результаты, совпадающие с практикой даже при вероятностном подходе, и с чем связано расхождение с классикой.
Доказательство практической необходимости наличия туннельного эффекта в квантовой механике связывают с холодной эмиссией, поэтому разберём, что же послужило причиной такого понимания. Вначале остановимся на таком явлении как фотоэффект [6, с. 34]. Отметим, что фотоэффектом называется испускание электронов веществом под действием света. Это явление было открыто Г. Герцем в 1887 г. В 1898 г. Леонард и Томсон провели усовершенствованный опыт (рис. 3).
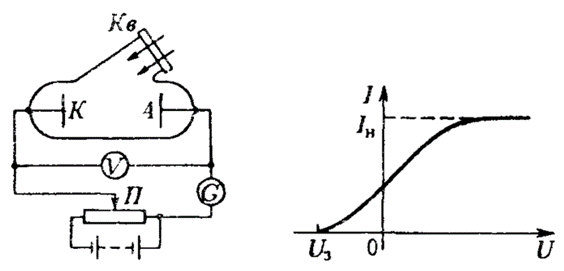
Рис. 3. Опыт по фотоэффекту
Пологий ход кривой на рисунке 3 указывает на то, что электроны вылетают из катода с различными по величине скоростями. Доля электрона, отвечающая силе тока при U = 0, обладает скоростями, достаточными для того, чтобы долететь до анода «самостоятельно», без помощи ускоряющего поля. Для обращения силы тока в нуль нужно приложить задерживающее напряжение Uз. При таком напряжении ни одному из электронов, даже обладающему при вылете из катода наибольшим значением скорости vm, не удается преодолеть задерживающее поле и достигнуть анода. Поэтому можно написать, что:
![]() (1)
(1)
где m0 – масса электрона. Таким образом, измерив, задерживающее напряжение Uз, можно определить максимальное значение скорости фотоэлектронов. Собственно, сам эффект подобен явлению Зеебека [7, с. 215] с той лишь разницей, что в этом случае вместо второго разнородного материала выступает вакуум.
К 1905 г. было выяснено, что максимальная скорость фотоэлектронов не зависит от интенсивности света, а зависит только от его частоты ‒ увеличение частоты приводит к возрастанию скорости. Установленные экспериментально зависимости не укладываются в рамки классических представлений. Например, скорость фотоэлектронов по классическим понятиям должна возрастать с амплитудой, а, следовательно, и с интенсивностью электромагнитной волны. Собственно вывод, о том, что есть противоречие с классикой и интенсивность не может влиять на скорость, является надуманной, так как если приложить к веществу напряжённость постоянного электрического поля, то мы будем наблюдать ток, что видно по холодной эмиссии. Суть независимости от напряжённости связана именно с переменным электромагнитным полем при отсутствии нагрева, так как положительные значения волны компенсируют отрицательные значения, а вот частота обеспечивает резонанс электронов на соответствующих уровнях, что и даёт выход фотоэлектронов. То есть противоречий с классикой нет, если учитывать резонансные явления перехода электронов с одной орбиты на другую.
В 1905 г. Эйнштейн показал, что все закономерности фотоэффекта легко объясняются, если предположить, что свет поглощается такими же порциями hf (квантами), какими он, по предположению Планка, испускается. По мысли Эйнштейна, энергия, полученная электроном, доставляется ему в виде кванта hf, который усваивается им целиком. Часть этой энергии, равная работе выхода W, затрачивается на то, чтобы электрон мог покинуть вещество. Если электрон освобождается светом не у самой поверхности, а на некоторой глубине, то часть энергии, равная Е0*, может быть потеряна вследствие случайных столкновений в веществе. Остаток энергии образует кинетическую энергию Ек электрона, покинувшего вещество. Энергия Ек будет максимальна, если Е*0=0. В этом случае должно выполняться соотношение:
![]() (2)
(2)
Это соотношение называется формулой Эйнштейна. Из формулы (2) следует условие, что для возникновения фотоэффекта необходимо выполнение условия:
![]() (3)
(3)
Частота f0 называется красной границей фотоэффекта. Заметим, что лишь малая часть квантов передаёт свою энергию фотоэлектронам. Энергия остальных квантов затрачивается на нагревание вещества, поглощающего свет. Собственно здесь нет противоречий с классической физикой, если рассматривать простейшую модель металла как свободный электронный газ, движущийся в потенциальной яме по рисунку 1 внутри которой потенциальная энергия V = 0, а вне, то есть в вакууме, V = V0 > 0.
Понятно, что здесь необходимо также обосновать значение потенциальной энергии для потенциальной ямы в которой находится так называемый электронный газ, что будет рассмотрено несколько ниже. Однако, по версии учёных, в классической теории модель «электронного газа», применяемая в теории газов, встретила большие затруднения при построении теории теплоёмкости. Суть здесь в том, что при версии «электронного газа», согласно известной теореме классической статистической механики о равномерном распределении энергии по степеням свободы, средняя кинетическая энергия электрона равна:
![]() (4)
(4)
где kб – постоянная Больцмана.
Отсюда видно, что доля каждого свободного электрона в общей теплоёмкости такая же, как и свободного атома:
![]() (5)
(5)
Это противоречит экспериментальным фактам, согласно которым теплоёмкость одноатомного металла определяется лишь теплоёмкостью атомов решётки, то есть свободные электроны в первом приближении никакого вклада в теплоёмкость металла не вносят. Собственно расхождение с классикой для свободного электронного газа связано с тем, что электроны нижних слоёв в атоме не имеют свободного движения, как это можно было рассматривать при «электронном газе», а значит, не могут иметь соответствующую скорость, зависящую от температуры. Это противоречие было разрешено Зоммерфельдом, который показал, что к электронам в металле необходимо применить не классическую статистику «электронного газа» с функцией распределения:
![]() (6)
(6)
а статистику Ферми-Дирака с функцией распределения:
![]() (7)
(7)
Иными словами, благодаря значению А функция распределения для свободных электронов ограничивается. Принцип получения данной функции распределения основывается на следующих предположениях [8, с. 178]. При абсолютном нуле в каждом из состояний, энергия которых не превышает ЕF(0), находится один электрон; в состояниях с Е > ЕF(0) электроны отсутствуют. Следовательно, функция распределения электронов по состояниям с различной энергией имеет при абсолютном нуле вид, показанный на рисунке 4.

Рис. 4. Распределение электронов в веществе при температуре абсолютного нуля [9, с. 147]
Однако, наличие температуры Т = 0 возможно только с точки зрения наличия электромагнитного вакуума [9, с. 147], так как в рамках теории Шредингера можно объяснить лишь вынужденные переходы, происходящие в результате взаимодействия электронов атома с внешней электромагнитной волной. Спонтанные же переходы, из возбуждённых энергетических состояний в более низкие состояния, как это признаётся в квантовой механике, остаются в этом случае фактически необъяснёнными, поскольку отсутствует внешнее воздействие, которое могло бы привести к этим переходам. Действительно, если атом не излучает, то, следовательно, электрон не может потерять энергию. То есть атомы в случае наличия электронов на дискретных орбитах (в квантовой механике это оболочки в виде орбиталей) не могут излучать, в силу постулатов Бора и отсутствия определённости в кинетической и потенциальной энергии атомов. Вакуум, как «пустота» по современной классике, в случае отсутствия в нём частиц, также не может формировать классические электромагнитные волны, так как нет противоположностей в виде зарядов. Соответственно здесь кроется парадокс, при котором атом по вероятностной квантовой механике не может излучать на дискретных орбитах нахождения электронов, одновременно нет в вакууме (как пустоты), и способов получения электромагнитной волны из ничего. И естественно, чтобы выйти из этого парадокса придумали виртуальные фотоны, которые образуются и исчезают в так называемом электромагнитном вакууме (пустоте) по принципу неопределённости Гейзенберга. То есть учёные утвердили чудо возникновения из ничего и исчезновения в ноль.
Иными словами, если закон сохранения количества нарушается в промежутки времени сопоставимые с выполнением соотношения неопределённостей Гейзенберга, то это, мол, не означает нарушение законов физики. Понятно, что наша теория [10] позволила разрешить это противоречие, но для этого потребовалось развить как философию, так и физику с математикой. При этом вакуум не является пустотой, а представляет собой взаимодействие объектов из двух противоположностей, отражённых через время и длину, что интерпретируется как наличие зарядов в соответствии с трактовкой Фейнмана при определении им связи силы Лоренца с силой Кулона. Это даёт электромагнитный континуум [11, с. 5-28] в сочетании с пространственно-временным континуумом с наличием взаимосвязи между элементами времени и длины (представлены зарядами с подчинением СТО Эйнштейна) через обмен электромагнитными составляющими. При этом находит объяснение принцип Гюйгенса-Френеля при огибании волной препятствия и искривлении прохождения света в так называемом гравитационном поле (пространственно-временное искривление по СТО и ОТО Эйнштейна). Соответственно в нашем случае всегда есть взаимодействие атомов вещества с так называемым вакуумом в виде пространства и времени через обмен электромагнитными составляющими с получением состояния термодинамического равновесия в соответствии с формулой Планка.
Таким образом, в отличие от вероятностной квантовой механики, у нас температура, связанная с условием термодинамического равновесия по формуле Планка между противоположностями длины и времени, так называемого вакуума, есть всегда. Соответственно здесь не требуется чудом возникающая в атоме нулевая энергия Е0 = 1/2hf, по соотношению неопределённостей Гейзенберга. И это связано с необходимостью и непрерывностью процесса обмена в динамике всех объектов Мироздания, какими также являются пространство и время. В противном случае будут объекты, полностью замкнутые на себя и такие объекты ни с чем не взаимодействуют, а значит, не могут быть обнаружены. Понятно, что наличие таких констант как электрическая и магнитная проницаемость, характеризующие пространство и время при пустоте (вакууме) в уравнениях Максвелла просто бы не могли существовать. Поэтому рисунок 4 с наличием температуры равной нулю представляет собой некоторую абстракцию.
С учётом сказанного найдём функцию распределения электронов в веществе при температуре, отличной от нуля. В квантовой механике следуя Кителю [12, с. 789] рассматриваются неупругие столкновения равновесного электронного газа с атомом примеси (фактически столкновения с передачей или отдачей энергии), внедрённым в кристаллическую решётку металла. В этом случае допускается, что атом примеси может находиться лишь в двух состояниях, энергию которых полагают равным 0 и ε. Понятно, что состояние с энергией равной 0 является некоторой абстракцией даже по вероятностной квантовой механике, где Е0 = 1/2hf. Из множества процессов столкновений рассматривается тот, в результате которого электрон переходит из состояния k с энергией Е в состояние k*с энергией Е+ε. Атом примеси переходит при этом с уровня с энергией ε на уровень с энергией, равной нулю. Вероятность перехода k(Е)→k*(Е+ε) пропорциональна:
- вероятности fр(ε) того, что состояние k (Е) занято электроном;
- вероятности [1‒fр(E+ε)] того, что состояние k* (Е+ε) свободно;
- вероятности р(ε) того, что атом примеси находится в состоянии с энергией ε.
Таким образом:
![]() (8)
(8)
здесь знак ![]() означает пропорциональность. Вероятность обратного процесса пропорциональна выражению:
означает пропорциональность. Вероятность обратного процесса пропорциональна выражению:
![]() (9)
(9)
где р(0) – вероятность того, что атом примеси находится в состоянии с энергией равной нулю. Еще раз подчеркнём, что такого состояния с энергией равной нулю нет и в квантовой механике, нулевая энергия атома равна Е0 = 1/2hf. В противном случае в вероятностной квантовой механике электрон упал бы на ядро. Иными словами, мы имеем некоторый начальный нулевой уровень отсчёта.
Далее предполагается принцип детального равновесия, согласно которому в состоянии статистического равновесия число переходов системы из состояния 1 в состояние 2 равно числу обратных переходов из состояния 2 в состояние 1. Отсюда в равновесном состоянии вероятности переходов k→k* и k*→k должны быть одинаковыми. Следовательно,
![]() (10)
(10)
отсюда имеем:
![]() (11)
(11)
здесь учитывается, что вероятности нахождения примеси на уровнях 0 и ε подчиняются закону распределения Больцмана. Функциональное уравнение (11) должно выполняться при любой температуре Т. Это произойдёт, если положить:
![]() (12)
(12)
где μп – величина, не зависящая от Е. Фактически, с помощью величины μп сделали нормировку.
Как мы показывали в [2, с. 5-26], между глобальными противоположностями существует термодинамическое равновесие, связанное с распадом в одной противоположности и синтезом в другой противоположности в виде уравнения: ![]() что соответствует формуле Планка
что соответствует формуле Планка ![]() . Введение величины μп соответственно изменяет уровень в функции распределения Больцмана. В результате получим:
. Введение величины μп соответственно изменяет уровень в функции распределения Больцмана. В результате получим:
![]() (13)
(13)
Понятно, что произведение выражений (12) и (13) при любой температуре равно ![]() . То есть определяется энергетическим уровнем перехода, но при этом из-за значения μп рассматриваем равновесное распределение относительно иного уровня. Иными словами, как бы исключаем из обмена и взаимодействия некоторые нижележащие уровни для электронов. Решив уравнение (12) относительно fр(E), получим для функции распределения электронов по состояниям с различной энергией выражение:
. То есть определяется энергетическим уровнем перехода, но при этом из-за значения μп рассматриваем равновесное распределение относительно иного уровня. Иными словами, как бы исключаем из обмена и взаимодействия некоторые нижележащие уровни для электронов. Решив уравнение (12) относительно fр(E), получим для функции распределения электронов по состояниям с различной энергией выражение:
![]() (14)
(14)
Это выражение называется функцией распределения Ферми-Дирака. Параметр μп носит название химического потенциала. Одновременно имеющий размерность энергии параметр μп часто обозначается через ЕF и называется уровнем Ферми или энергией Ферми.
В соответствии со смыслом функции (14) величина fр(E) представляет собой среднее число электронов <nμ>, находящихся в состоянии с энергией Е. Поэтому формуле (14) можно придать вид:
![]() (15)
(15)
при этом параметр ЕF имеет положительные значения. Соответственно распределение электронов при уровне Ферми показано на рисунке 5.
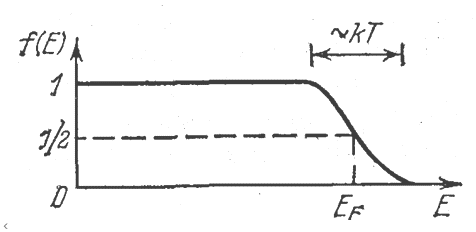
Рис. 5. Распределение электронов при уровне Ферми [13, с. 75]
Физический смысл уровня Ферми в квантовой механике выводится из следующих соображений [13, с. 75]. Предполагается наличие трёхмерной потенциальной ямы кубической формы с длиной стороны L, при этом составляющие импульса ри=ћk, будут связаны с целыми числами n1, n2, n3 характеризующими энергетический уровень соотношениями:
![]() (16)
(16)
далее учитывается, что на единичный интервал квантовых чисел (∆n1=∆n2=∆n3=1). Отсюда имеем:
![]() (17)
(17)
при этом на один уровень приходится лишь два электрона.
Поэтому, если в единице объёма находится ρ0 электронов, то максимальный импульс, которым может обладать электрон при абсолютном нуле температуры (Т=0) с учётом нахождения двух электронов на одном уровне, определяется из соотношения:
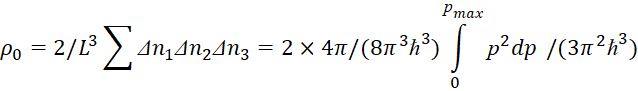 (18)
(18)
отсюда имеем:
![]() (19)
(19)
соответствующая максимальная кинетическая энергия электронов равна:
![]() (20)
(20)
Мы видим, что здесь расчёт максимальной кинетической энергии в атомах приравнивается к уровню Ферми при температуре равной нулю, что соответствует рисунку 4. При этом схема заполнения электронных уровней в металле изображена на рисунке 6.
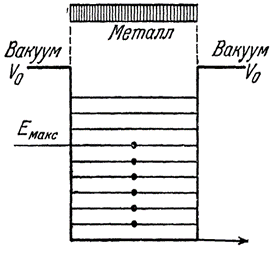
Рис. 6. Модель потенциальной ямы для металла. Емакс – верхняя граница заполненных уровней при Т = 0 (энергия Ферми)
Понятно, что здесь парадокс уже в том, что нет способа определения, каким образом и откуда берётся энергия для электронов в атоме для достижения уровня Ферми и выше уровня нулевой энергии по соотношению неопределённостей Гейзенберга. Если из вакуума, то есть пустоты, то это ‒ чудо, так как передача энергии от возникающих виртуальных фотонов должна сопровождаться таким же отъёмом энергии по закону сохранения количества энергии. В противном случае вакуум должен обладать резервуаром кинетической энергии, но тогда должна быть реальная материальная основа, а при пустоте её нет.
В нашей теории вакуум не пустота, и он состоит из объектов Мироздания, выраженных через пространственно-временное искривление со связью элементов через электромагнитные составляющие от электронных и мюонных нейтрино (антинейтрино), и в этом случае есть материальная основа для кинетической энергии по формуле Планка.
В принципе определение уровня энергии Ферми велось с использованием чисто классических основ физики. Поэтому оценим значение энергии Ферми, например, для серебра. Плотность серебра равна 10,5, атомный вес 107,9. Считая, что число свободных электронов равняется числу атомов серебра в единице объёма, имеем:
![]() (21)
(21)
здесь используется число Авогадро, то есть число атомов в одном грамм-атоме, равное 6,02х1023. Отсюда по формуле (20) находим, что:
![]() (22)
(22)
Теперь можно объяснить, почему электронный газ вносит очень малый вклад в теплоёмкость металлов. Средняя тепловая энергия, равная по порядку величины kT, составляет при комнатной температуре 1/40 эВ. Такая энергия может возбудить только электроны, находящиеся на самых верхних уровнях, примыкающих к уровню Ферми. Основная масса электронов, размещённых на более глубоких уровнях, останется в прежних состояниях, и поглощать энергию при нагревании не будет. Таким образом, в процессе нагревания металла участвует лишь незначительная часть электронов проводимости, чем и объясняется малая теплоёмкость электронного газа в металлах. Пользуясь известным определением среднего значения энергии электрона в металле при Т = 0 получим выражение:
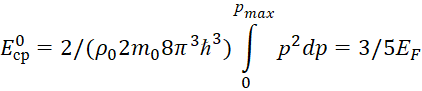 (23)
(23)
Поскольку для серебра работа выхода W = 3,7 эВ, то глубина потенциальной ямы в серебре оказывается равной V0 = 9 эВ. Исходя из описанной модели (рис. 6), мы видим, что для вырывания электрона из металла необходимо сообщить ему энергию, не меньшую, чем работа выхода:
![]() (24)
(24)
При этом электрон может покинуть металл, обладая кинетической энергией по формуле (2). Отсюда следует, что работа выхода W есть минимальная энергия, которую нужно затратить, чтобы энергия электрона стала больше высоты потенциального барьера. Однако, от чего зависит значение работы выхода W и за счёт чего образуется потенциальная яма? Вероятностная квантовая механика не может дать ответа на этот вопрос в силу того, что мы имеем вариант орбиталей (оболочек) электрона в атоме по рисунку 7.
Рис. 7. Орбитали для атомов
При этом в силу неопределённости значения импульса исключается излучение электронов на орбиталях. Действительно, как известно электрические силы от одного заряда замыкаются на другом заряде (рис. 8), то есть атом представляет собой статическую модель с отсутствием электрического поля вне оболочки.
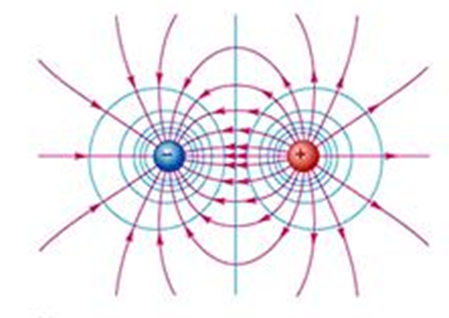
Рис. 8. Взаимодействие двух зарядов
Действительно, если бы атом имел бы вне оболочки положительный заряд (на рисунке 1 – это значение V→∞, а на рисунке 2 это уже значение V0), то было бы отталкивание атомов друг от друга за счёт положительного заряда. Если бы атом имел отрицательный заряд, то шло бы отталкивание атомов за счёт отрицательного заряда. Иными словами, математическая модель с наличием поля для потенциальной ямы, связанного с зарядами, абсурдна с самого начала, что означает, что силовые линии всегда замыкаются с одного заряда на другой. Ещё одним парадоксом в вероятностной квантовой механике является то, что динамика изменения местоположения электрона в вероятностной оболочке за счёт телепортации должна бы приводить к изменению силовых электрических линий в пространстве. А это не может происходить быстрее скорости света, и запаздывание, в соответствии с законами электродинамики, должно приводить к излучению.
Таким образом, вероятностная модель орбиталей электронов является абсурдной изначально. Отсюда мы вновь приходим к необходимости варианта нашей теории с обеспечением взаимодействия на основе электронных и мюонных нейтрино (антинейтрино) с преобразованием кинетической энергии в потенциальную энергию и, наоборот, в соответствии с усовершенствованными уравнениями Максвелла ‒ от простого к сложному [14, с. 32-58].
Однако, каким образом происходит удержание электронов в веществе, если сами атомы являются электрически нейтральными? Понятно, что в этом случае взаимодействие за счёт обмена между так называемыми противоположными зарядами в веществе должно быть выше, чем взаимодействие с внешними объектами. Соответственно ставится вопрос, а за счёт чего такой обмен внутри вещества выше? По нашей теории [10] пространственно-временное искривление, которое характеризует потенциальную энергию в одной противоположности, в другой противоположности представляется кинетической энергией в соответствии с СТО и ОТО Эйнштейна. Это означает, что в этом случае из-за пространственно-временного искривления большей величины, чем это есть в вакууме, есть избыток электронных и мюонных нейтрино (антинейтрино) при обмене между так называемыми противоположными зарядами, что позволяет удерживать электроны, находящиеся выше уровня Ферми. И вот именно эта дополнительная энергия обмена и представляет так называемую энергию (работу) выхода.
Собственно, на наличии пространственно-временного искривления на основе констант электрической и магнитной проницаемости, которые в нашей теории связаны с формулами СТО и ОТО Эйнштейна и строится теория гравитации. Если увеличивать кинетическую энергию электронного газа путём нагревания металла, то некоторая часть электронов может иметь энергию, превышающую потенциальную энергию обмена, благодаря чему возникает ток из металла. Это явление получило название термоэлектронной эмиссии. Однако возникновение тока электронов возможно и при низких температурах под влиянием постоянного внешнего электрического поля напряжённости Эн, приложенного к поверхности проводника по направлению к ней (рис. 9).
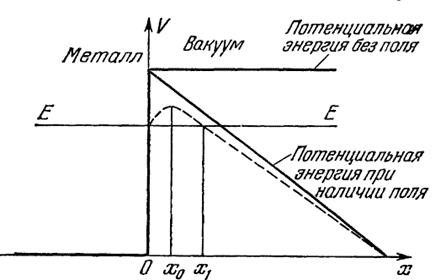
Рис. 9. Потенциальная энергия электрона в металле без поля и при наличии внешнего электрического поля. Штриховой линией показан ход потенциальной кривой с учётом сил электрического изображения
Выше мы отмечали, что некорректно говорить о наличии потенциальной ямы в виде электрического поля вне атома, однако, мы сейчас рассматриваем парадоксы, допущенные в классической и квантовой механике. Поэтому будем придерживаться подхода, сделанных в этих теориях и разъяснять противоречия, допущенные в них. В этом случае, в соответствии с рисунком 9, потенциальная электрона заряда (-е0) равна:
![]() (25)
(25)
Далее делается предположение, что помимо внешнего электрического поля на электрон действует так называемая сила электрического изображения. То есть здесь рассматривается вариант, когда электрон, обладая зарядом (-е0) создаёт в металле индуцированный заряд (+е0) (рис. 10).
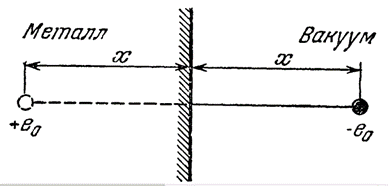
Рис. 10. Силы электрического изображения: на находящийся вне металла электрон действуют силы притяжения индуцированным зарядом
Полная сила, действующая на электрон в металле, при этом вычисляется по формуле:
![]() (26)
(26)
Иными словами, имеется противодействие выходу электрона из металла за счёт силы электрического изображения.
Понятно, что такой подход с наличием сил электрического изображения был бы правильным, если не было приложения к металлу внешнего электрического поля. Действительно, приложение к металлу внешнего электрического поля, а в данном случае эту роль представляют электрические заряды вне металла, будет приводить к возникновению в металле эллиптических орбит с наличием электрических диполей (рис. 11).
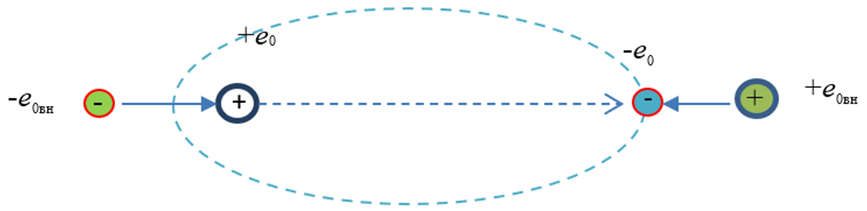
Рис. 11. Создание электрических диполей с эллиптическим движением по орбите электрона вокруг протона при наличии внешнего электрического поля Эн
Иными словами, при наличии внешнего электрического поля никаких сил электрического изображения быть не может, а прилагаемое к металлу внешнее электрическое поле внутри металла (при компенсации внешнего электрического поля), должно приводить к ослаблению обмена между положительными и отрицательными зарядами из-за эллиптических орбит, что способствует снижению работы выхода электронного газа в металле. При этом влияние внешнего электрического поля происходит на все электроны в атоме вещества (формируются диполи), а не только на электронный газ верхних оболочек.
Таким образом, в формуле (26) не учитывается ослабление величины работы выхода за счёт получения эллиптических орбит на всех слоях, так как время связи, с ослаблением самой связи, при обмене на больших расстояниях увеличивается пропорционально смещению х получаемому в эллипсе (по сравнению с круговыми орбитами), а на малых расстояниях уменьшается. Это связано с тем, что заряды являются константами и по нашей теории определяют количественную характеристику обмена электронными и мюонными нейтрино (антинейтрино) в соответствии с системой усовершенствованных уравнений Максвелла, замещающих систему уравнений Дирака в квантовой механике [14, с. 32-58]. Так как количество элементарных объектов (электронных и мюонных нейтрино и антинейтрино) при обмене ограничено (иначе заряд не константа), то соответственно усиленный обмен с внешними зарядами электрического поля может происходить только за счёт ослабления обмена с внутренними противоположными зарядами в атомах металла. Это должно приводить к дополнительной зависимости работы выхода от напряжённости внешнего электрического поля в виде зависимости W(Эн).
Для варианта, рассмотренного для классического подхода в квантовой механике, внешнее электрическое поле не влияет на работу выхода, то есть, по сути, имеем вариант исключения представления зарядов как констант, что связано с бесконечным числом элементарных объектов для обмена между противоположными зарядами, чего не наблюдается. При этом для классического подхода в квантовой механике эффективная потенциальная энергия, учитывающая силы электрического изображения, была вычислена по формуле:
![]() (27)
(27)
соответственно здесь считается, что величина Vэфф имеет максимум в точке х0 (рис. 9):
![]() (28)
(28)
отсюда:
![]() (29)
(29)
причём максимальное значение Vэфф меньше V0, так как:
![]() (30)
(30)
В итоге, на основе взаимодействия только электронного газа за счёт сил так называемого электрического изображения была вычислена величина напряжённости электрического поля по формулам:
![]()
![]() (31)
(31)
Однако на опыте достаточно сильный ток появляется уже при поле Эн~4х105 В/см (Милликен). Отсюда посчитали, что в рамках классической теории на основе сил электрического изображения невозможно объяснить с количественной стороны явление холодной эмиссии. Соответственно далее пошли по пути чудес через прохождение электрона сквозь потенциальный барьер [15, с. 71] на основе метода сшивания решений.
Как мы увидим далее, благодаря коэффициенту прозрачности D, при прохождении через потенциальный барьер, фактически была введена зависимость работы выхода от напряжённости внешнего электрического поля. При этом ни о каких силах «электрического изображения» при выводе коэффициента прозрачности речи не шло. О парадоксах связанных со сшиванием решений мы уже говорили в [2, с. 5-26]. Ниже мы также продолжим вскрывать парадоксы при использовании туннельного эффекта.
Рассмотрим потенциальный барьер прямоугольной формы высоты V0, и ширины, а (рис. 2). Барьер такой формы интересен в том отношении, что для него задача о туннельном эффекте (как считается в квантовой механике) допускает точное и вместе с тем простое решение. Кроме того, на его примере можно исследовать так называемое над барьерное отражение, когда энергия частицы Е больше высоты барьера (Е>V0).
Пусть частица, энергия которой меньше высоты барьера (Е<V0), движется в условном положительном направлении оси х. Тогда решения уравнения Шредингера [16] для каждой из трёх областей имеют вид:
![]()
![]() (32)
(32)
![]()
здесь:
![]() (33)
(33)
При этом коэффициент перед падающей волной eikx за счёт выбора нормировки положен равным единице. При этом величина В1eikx характеризует отражённую волну, а справа от барьера (x>a) присутствует только прошедшая волна А3eikx.
Здесь отметим, что попытка представления движения частицы по рисунку 2 в виде падающей, отражённой и прошедшей волны имеет абстрактный характер, так как из волновой функции должна получаться величина вероятности нахождения частицы в том или ином месте. Соответственно одномерная и даже трёхмерная модель движения частицы не вписывается в условие движения без ускорений, что означает необходимость излучения и поглощения электромагнитной кинетической энергии.
Таким образом, даже при наличии неопределённости Гейзенберга для импульса изменение положения частицы должно сопровождаться изменением электрического поля между противоположными зарядами с соответствующим излучением. Кроме того, по рисунку 2 отражённая волна меняет фазу на отрицательное значение относительно энергии Е. Если под волновой функцией Ψ понимать связь с вероятностью, то по логике мы должны иметь вариант, когда сумма от вероятностей отражённой и проходящих волн, должна равняться вероятности падающей волны. Собственно такой подход диктуется из характеристики величины туннельного эффекта через введение коэффициента прозрачности барьера, под которым понимается модуль отношения плотности потока частиц, прошедших через барьер к плотности потока падающих частиц:
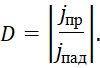 (34)
(34)
если теперь ввести коэффициент отражения, то имеем:
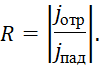 (35)
(35)
из сравнения формул (34) и (35) следует, что сумма коэффициента прозрачности и коэффициента отражения равна единице:
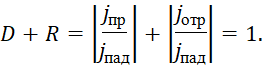 (36)
(36)
при этом для определения потока частиц используется формула:
![]() (37)
(37)
здесь Ψ* ‒ комплексно-сопряжённая функция к Ψ.
Понятно, что сама формула (37) также имеет парадоксы, что было нами показано в [2, с. 5-26] в силу того, что перемножение комплексно-сопряжённых величин волновых функций Ψ(r)×Ψ*(r)=e‒ikr×eikr=e0=1 (это также получено и в квантовой механике). И здесь видно, что нет никакой зависимости константы от вероятности. То есть мы имеем плотность тока на основе движения заряженной частицы в двух направлениях в границах потенциальной ямы. Поэтому утверждение Борна, что под произведением Ψ(r)Ψ*(r) следует понимать плотность вероятности нахождения частицы в точке пространства с радиус-вектором r, означает абсурд.
Однако продолжим исследование решения на основе вероятностной квантовой механики. Для определения неизвестных коэффициентов в решении (32) используют условие непрерывности волновой функции и её первой производной на границах барьера.
При х=0 имеем:
![]()
![]() (38)
(38)
При х=а имеем:
![]()
![]() (39)
(39)
из последних двух уравнений находим:
![]()
![]() (40)
(40)
подставим А2 и В2 в уравнения (38) и исключая В1, получаем:
![]() (41)
(41)
коэффициент прохождения D можно вычислить по общей формуле (34), используя коэффициент (41):
![]()
![]() (42)
(42)
для достаточно широкого барьера, ![]() , из точного выражения (42), приближённо находим:
, из точного выражения (42), приближённо находим:
![]() (43)
(43)
при соответствующем значениях Е и V0 можем получить значение D0 порядка единицы.
Подставляя в (43) значение из (33), можно коэффициент D записать в виде ():
![]() (44)
(44)
данный результат можно представить в виде:
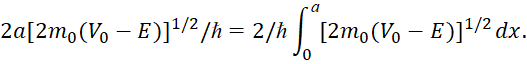 (45)
(45)
последний вариант записи позволяет иметь зависимость V0 и E от х.
Из формулы (44) видно, что чем больше ширина потенциального барьера a, тем меньше величина D. Однако в этом случае снова имеем алогизм, связанный с тем, что плотность проходящего тока падает в интервале от х=0 до х=а, но при этом нет других преобразований или изменения направления плотности тока. Иными словами, получаем что заряды, характеризующие плотность тока, должны в потенциальном барьере исчезать, что противоречит первому правилу Кирхгофа (правило токов Кирхгофа), которое гласит, что алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи, равна нулю. То есть зависимость плотности тока при телепортации в потенциальном поле барьера по формуле (37) ‒ это чистая абстракция.
Соответственно теперь перейдём к преодолению потенциального барьера по рисунку 9. Отличие здесь от прямоугольного барьера в том, что помимо энергии Е вводится ещё зависимость от значения напряжённости электрического поля Эн. В этом случае коэффициент прозрачности равен:
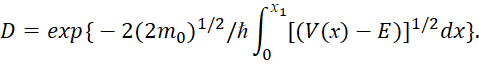 (46)
(46)
интеграл в экспоненте должен быть взят по всей ширине барьера от точки х=0 до точки х=х1, которая определяется из условия:
![]() (47)
(47)
Иными словами, из формулы (47) следует, что значение ширины барьера х1 выбирается из условия равенства работы выхода W и величины е0Эн, в то время как по классике с привлечением силы так называемого «электрического изображения» (приведённой в формуле (29)), эта величина полностью зависит от значения Эн. Это означает, что если расчёт по формуле (47) с целью определения напряжённости электрического поля Эн связан с преодолением величины работы выхода W, то расчёт по формуле (29) опирается на вычисление Эн, связанного с преодолением величины силы кулоновского притяжения e02/(4x02) на основе сил «электрического изображения».
Однако подход по классике формулы (29) был бы приемлем, если бы дело касалось электронов на орбитах, а не в виде электронного газа, когда значение kT уже обеспечивает преодоление этих сил и остаётся лишь преодолеть значение работы выхода. С учётом (47), когда уже значение х1 выбрано таким образом, что напряжённость электрического поля соответствует работе выхода, мы получаем:
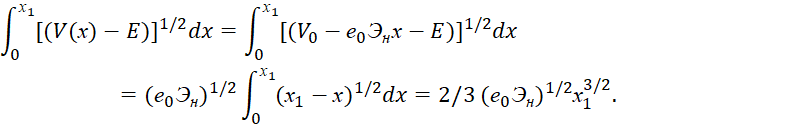 (48)
(48)
окончательно для коэффициента прозрачности D получаем выражение:
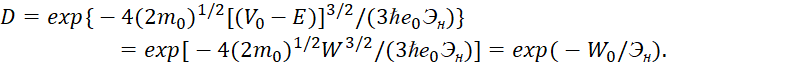 (49)
(49)
здесь W0 – зависит от работы выхода W из металла свободных электронов (электронного газа).
Свободные электроны, преодолевшие барьер работы выхода, составляют ток холодной эмиссии пропорционально вычисленному коэффициенту прозрачности D согласно формуле:
![]() (50)
(50)
отсюда следует, что холодная эмиссия должна наблюдаться при напряжённости электрического поля Эн~105 В/см, что хорошо согласуется с экспериментальными данными.
Полученный результат по формуле (50) можно считать чисто классическим, так как в коэффициенте прозрачности рассматривается вариант только на основе напряжённости электрического поля и работы выхода, и нет никакого преодоления потенциального барьера с телепортацией. Здесь значение х1 можно рассматривать как необходимое расстояние прохождения пути электроном для приобретения энергии, равной работе выхода за счёт ускорения электрона под воздействием напряжённости электрического поля.
Повторим, что ошибка учёных при рассмотрении классического подхода в квантовой механике касалась того, что вместо преодоления электрическим полем величины работы выхода, рассматривалась величина преодоления сил притяжения противоположных зарядов, что и дало разницу на два порядка. Экспоненциальная зависимость тока также определяется экспоненциальной зависимостью распределения электронов по уровням энергии, только вместо значения kT берётся зависимость от напряжённости электрического поля, которая в течение расстояния х1 обеспечивает разгон электронов электронного газа до величины, обеспечивающей преодоление работы выхода W. Иными словами, здесь уместно рассматривать сумму тепловой энергии kT с энергией электрического поля, обеспечивающей разгон электронов электронного газа до величины, обеспечивающей преодоление величины работы выхода.
Таким образом, если исходить из рисунка 5, то мы имеем как бы смещение уровня ЕF в сторону больших значений до уровня V0 за счёт энергии напряжённости электрического поля, пересчитанного в значение работы выхода W. Именно это и было сделано при вычислении коэффициента прозрачности, за счёт так называемого туннельного эффекта.
Отсюда следует вывод, что никаких парадоксов в классическом подходе нет. В вероятностном квантовом подходе с туннельным эффектом используется классический метод выхода электронов из металла на основе передачи кинетической энергии электронам от напряжённости электрического поля на промежутке длины х1 и равенством энергии выхода. Ошибка была связана с использованием сил «электрического изображения» в классическом методе, что дало разницу в представлении сил, действующих на электрон и соответственно разницу в результатах на два порядка.

.png&w=640&q=75)