Введение
Реверберационная камера (РК) была впервые введена Х. А. Мендесом в 1968 г. [5, с. 20-23]. Вот уже более 40 лет RC широко используется для широкого спектра радиочастотных приложений, таких как характеристика антенн и датчиков, измерения электромагнитных помех и восприимчивости (EMS) [4], характеристика поперечного сечения экранирования и поглощения (ACS) материалов [4], реализация среды многолучевого канала и беспроводные испытания будущих устройств 5G/6G [9, с. 49129-49143].
Для начала, РК можно представить, как прямоугольный резонатор с проводящими стенками. Когда в РК вводится энергия с помощью, например, передающей антенны, тогда будут возбуждаться собственные частоты, которые образуют трехмерные картины стоячих волн. Основными компонентами реверберационной камеры являются хорошо проводящая, большая экранированная металлическая конструкция с полостью, тюнер/мешалка, передающая и приемная антенны. Электромагнитная (ЭМ) среда внутри реверберационной камеры меняется с помощью различных методов перемешивания, таких как движение тюнера (настроенное на моду или перемешивание по моде), частотное перемешивание, вибрация проводящей ткани, изменение ориентации, поляризация или положение используемых антенн или испытательного оборудования (ИО). Для изменения модальной структуры внутри РК для генерации статистически однородных, изотропных и однородных пространственных ЭМ-полей внутри РК используется один или комбинация вышеупомянутых методов перемешивания.
Исследовательская часть
Метод расчета
Собственная частота прямоугольного резонатора может быть вычислена с помощью (1) [4].
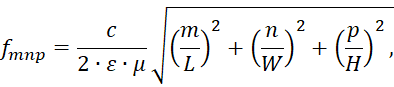 (1)
(1)
где m, n и p – целые числа, L, W и H – длина, ширина и высота металлической полости, c – скорость света, Ɛ – диэлектрическая проницаемость вакуума, µ - магнитная проницаемость вакуума.
На практике обычно LUF возникает на частоте, немного превышающей трехкратную частоту первого резонанса камеры. LUF также может быть выражен как; (I) частота, при которой внутри резонатора существует не менее 60–100 мод; (II) частота, при которой внутри резонатора присутствует не менее 1,5 моды/МГц (модальная плотность) [4; 6, с. 1-16]. Эти ограничения формируются для обеспечения достаточного количества собственных частот в РК для удовлетворения основных эксплуатационных требований статистически однородных полей.
«Недомодовый» резонатор – это случай, когда РК работает ниже LUF. Условие достаточного количества собственных частот или перемешивания возникает, когда РК работает на частотах выше LUF. Наличие большого количества режимов делает работу РК сверхмодовой. Обычно поле в «недомодованном» резонаторе считается таковым из-за наличия меньшего числа мод.
Обобщенная формула Вейля для расчета числа мод (N(f)) (2) или модальной плотности (m) (3) [7, с. 637-653] используется для грубой оценки LUF РК на основе его геометрических размеров.
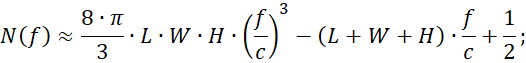 (2)
(2)
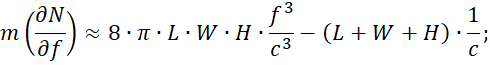 (3)
(3)
Коэффициент добротости (Q) представляет собой способность РК накапливать энергию по отношению к скорости его рассеивания. Q является важным параметром, характеризующим РК, поскольку он используется для различных приложений, таких как анализ загрузки камеры; усиление поля при измерении электромагнитной восприимчивости и другие.
На добротность камеры влияют четыре основные потери: (I) рассеивание мощности в стенах; (II) наличие поглощающего объекта в РК; (III) апертурная утечка; и (IV) рассеивание мощности в нагрузке приемной антенны [1; 2, с. 591-592; 3, с. 169-178]. Составной коэффициент качества (Q) для пустой камеры представляет собой комбинацию коэффициента добротности стенок и размещенных антенн, как показано в (4) [1; 2, с. 591-592; 8].
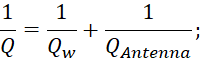 (4)
(4)
Существуют различные математические формулы для расчета теоретической добротности РК. В 1983 г. Liu и др. в работе [1] приводили выражение (5) для оценки добротности стенок камеры Q для прямоугольной полости. В (5) L, W, H – размеры камеры, V = LWH – объем камеры, S = 2 (WL + HL + HW) – площадь поверхности полости, δ = 1/√(πfσWµoµr) – глубина поверхности слоя, где σW – проводимость материалов стенок, k = ω/c. Позже, в 1996 г., Хилл [2, с. 591-592] предложил упрощенное выражение (7) с использованием разложения по плоской волне для РК произвольной формы с немагнитными стенками, т.е. µr = 0. Приведенное выражение [2, с. 591-592] проиллюстрировано в (6).
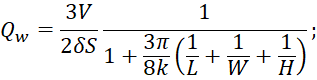 (5)
(5)
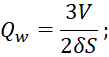 (6)
(6)
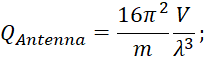 (7)
(7)
Besnier и др. [8] предложили простое выражении (7) для вычисления QAntenna. В (7) m представляет собой рассогласование антенн и равно 1 для случая согласованной антенны. Составную Q можно затем вычислить, используя (6) путем объединения QAntenna и QW.
Методика моделирования
Сравнение результатов будет производиться с помощью среды для ЭМ моделирования CST Studio Suite (рис. 1). Для решения данной задачи подходит «решатель» собственных мод, который используется для расчета частот и соответствующих моделей электромагнитного поля (собственных мод), когда возбуждение не применяется.
Собственные моды и их частоты являются решениями уравнения на собственные значения:
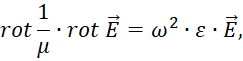 (8)
(8)
где ω – собственные значения и E – собственные векторы.
Моделирование производилось исходя из размеров РК с использованием тетраэдрической сетки (рис. 1).

Рис. 1. Модель РК в среде CST Studio Suite
Аналитическая часть
Собственные частоты
Собственная частота резонатора:
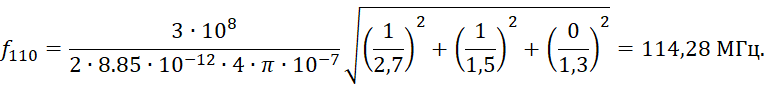 (9)
(9)
Нижняя рабочая частота реверберационной камеры, взятой для 3D моделирования – 400 МГц. Частота, при которой внутри резонатора существует не менее 100 мод (2), составляет 403 МГц (рис. 2). Частота, при которой внутри резонатора присутствует не менее 1,5 моды/МГц составила 558 МГц (рис. 3).
Таким образом, LUF лежит в диапазоне от 403–558 МГц.
Собственные колебания, найденные методом численного моделирования и используя выражение (1), изображены на рисунке 4.
Результаты моделирования и расчета практически полностью совпадают, что говорит о достоверности 3D модели.
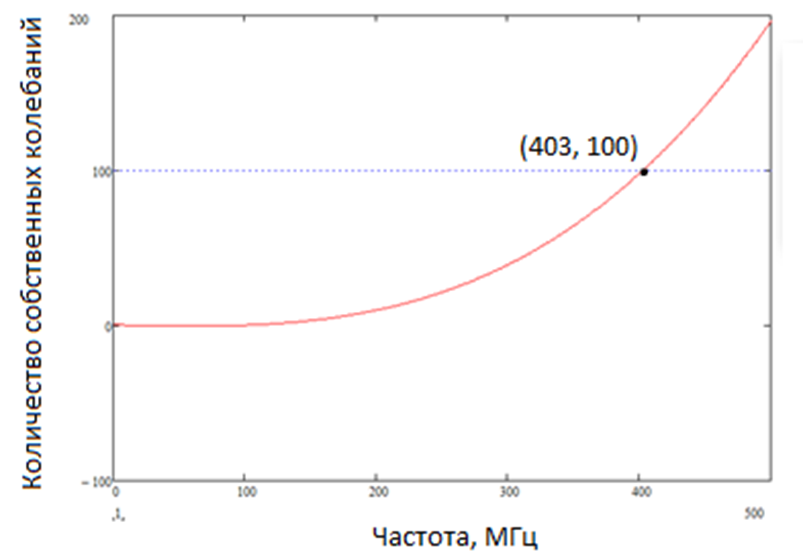
Рис. 2. График зависимости частоты от количества собственных колебаний
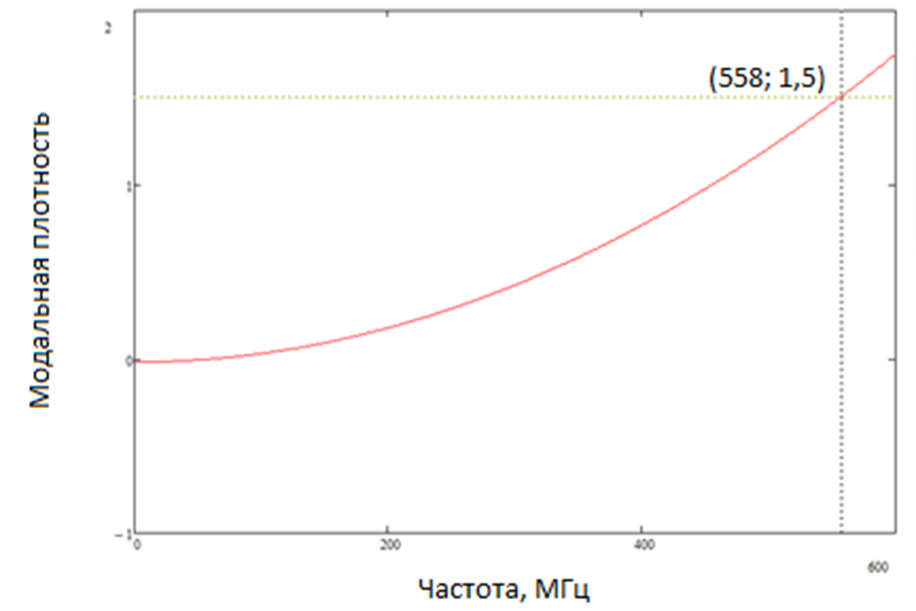
Рис. 3. График зависимости частоты от модальной плотности
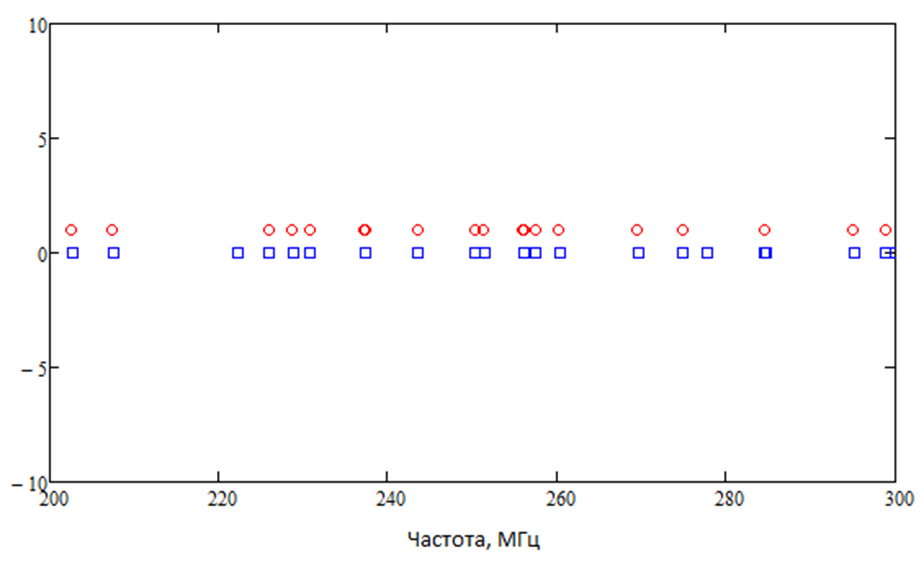
Рис. 4. График собственных колебаний реверберационной камеры в диапазоне частот 200–300 МГц (красным – собственные частоты, найденные численным моделированием; синим – собственные частоты, найденные выражением (1)).
Добротность РК
На рисунке 5 показано сравнение рассчитанных Qw с использованием и (5) и (6) при σW = 3,77e7 для алюминиевых стенок РК. При высокой частоте k становится больше, что упрощает (5) до (6), как видно из рисунка 5, где две кривые становятся идентичными по мере увеличения частоты. Результаты расчета составной добротности с включением коэффициента QAntenna (7) показаны на рисунке 6. На рисунке 5 видно, что низкочастотные различия между двумя кривые (рис. 6) уменьшаются за счет включения добротности антенны.
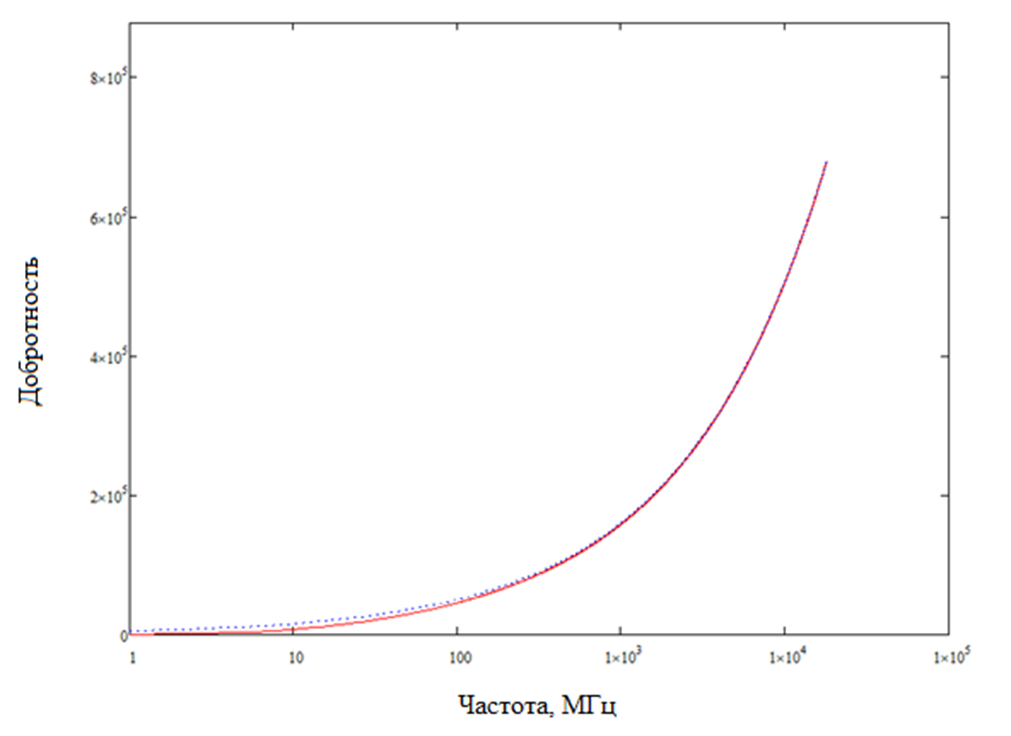
Рис. 5. Сравнение теоретической Q (синий – добротность, рассчитанная с помощью (5), красный – добротность, рассчитанная с помощью (6))
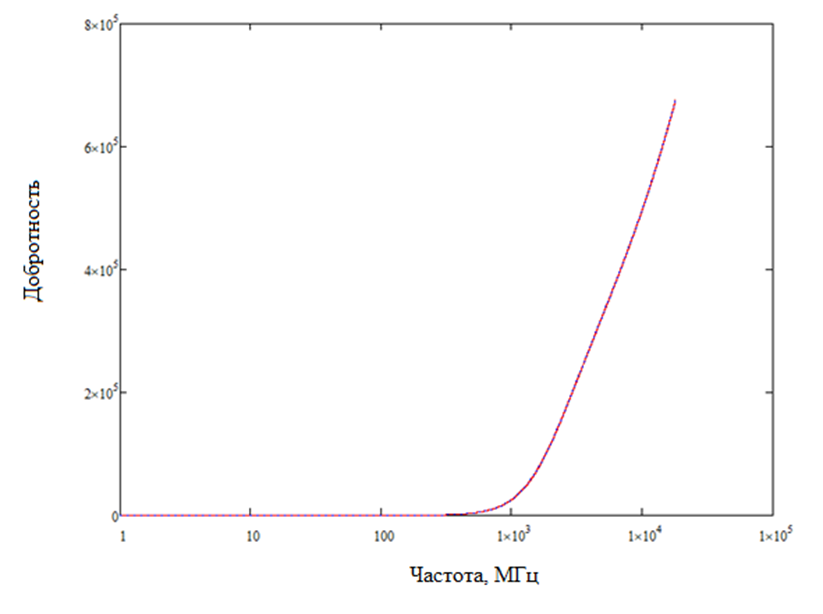
Рис. 6. Сравнение составного Q, используя (5), (6) и (7)
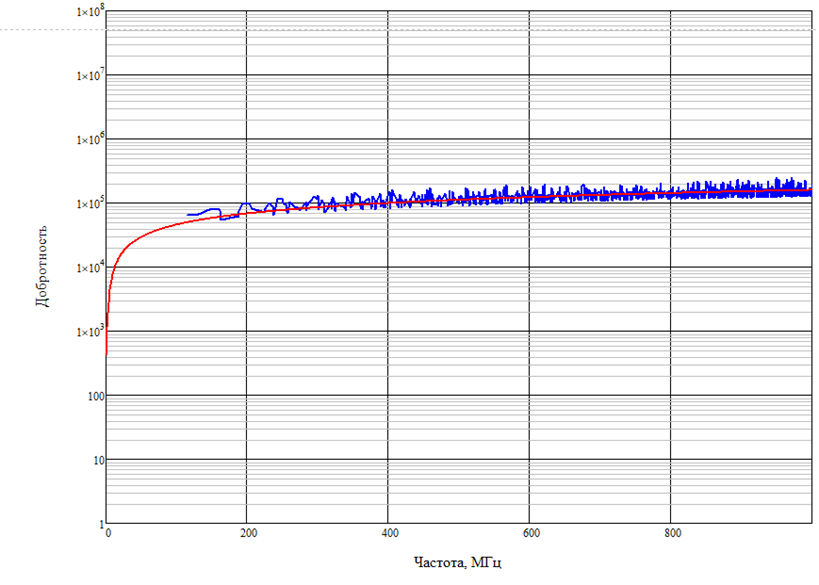
Рис. 7. График зависимости добротности реверберационной камеры от частоты в диапазоне частот до 1000 МГц (синий – добротность, найденная методом численного моделирования; красный – добротность, найденная методом расчета (5)).
Заключение
В данной работе произведен расчет собственных колебаний и добротности реверберационной камеры методом расчета и численного моделирования. Полученные результаты могут быть использованы для проектирования реверберационных камер с необходимыми характеристиками. Реверберационные камеры стали незаменимым инструментом для испытаний на ЭМС во многих отраслях промышленности. Проводя тщательное исследование устойчивости оборудования к потенциальным электромагнитным помехам и излучениям, они предоставляют разработчикам и инженерам бесценную информацию, что в конечном итоге повышает безопасность, производительность и надежность оборудования в различных отраслях.

.png&w=640&q=75)