В статье «Математическая модель для гибких тензодатчиков на основе токопроводящих порошков» [1] была описана математическая модель для гибкого тензометрического датчика на основе токопроводящих порошков. Для её проверки необходимо создать тестовый образец, с помощью которого получим зависимость сопротивления R от удлинения l.
Перед началом создания датчика был проведён поиск необходимых материалов. В ходе поисков для матрицы был выбран литьевой силикон с твёрдостью Шора равной 30 и плотностью 1,08 г/см3, так как его физико-механические свойства подходят под наши потребности, для наполнителя были выбраны порошки из: меди, алюминия и графита, из-за их электрических свойств. Так как было необходимо выбрать мелкодисперсные токопроводящие порошки, были выбраны следующие марки: медный порошок ПМР; алюминиевая пудра ПАП-1; графит литейный ГЛ-1.
После подбора материалов необходимо было создать литьевую форму. В программе «КОМПАС-3D» была создана литьевая форма, представленных на рисунке 1, с рабочей зоной 10×63×2 мм. После этого литьевая форма была создана с помощью 3D принтера.
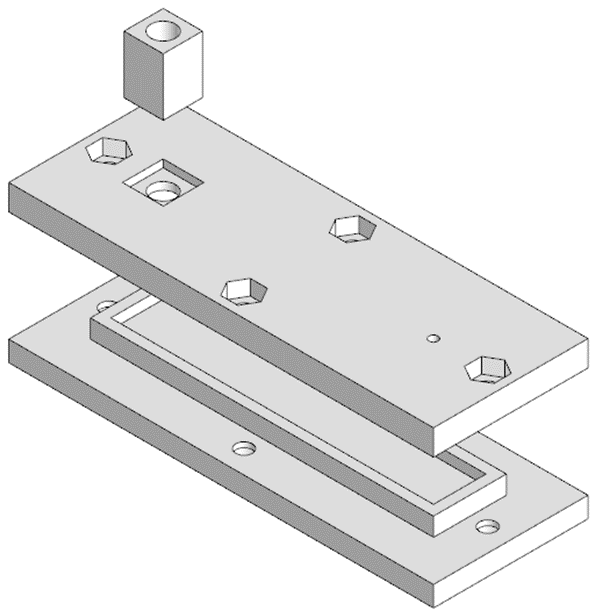
Рис. 1. Модель форма для заливки датчиков
Для создания датчика необходимо рассчитать отношение силикона и токопроводящих порошков. Для этого необходимо знать насыпную плотность порошков. По ГОСТ 4960-75 «Порошок медный электролитический. Технические условия.» насыпная плотность медного порошка составляет 4 г/см3, по ГОСТ 5494-95 «Пудра алюминиевая. Технические условия.» насыпная плотность алюминиевой пудры составляет ~ 0,22 г/см3, по ГОСТ Р 50019.1-92 «Графит. Метод определения насыпной плотности.» была получена насыпная плотность графита, рассчитана насыпная плотность по формуле:
![]() (1)
(1)
где:
m1 – масса ёмкости с графитом;
m2 – масса ёмкости;
V – объём ёмкости;
Насыпная плотность графитового порошка составила 0,87 г/см3.
Для замеса тестовых гибких тензометрических датчиков было взято 4 грамма литьевого силикона, для облегчения смешивания компонента А с компонентом Б. Объём силикона находится по формуле:
![]() (2)
(2)
где:
![]() – масса силикона;
– масса силикона;
![]() – плотность силикона;
– плотность силикона;

Рис. 2. Гибкие тензонометрические датчики на основе графитового, медного и алюминиевого порошков
Затем была рассчитана масса порошка, входящего в гибкий тензометрический датчик, по формуле:
![]() (3)
(3)
где:
V – объём силикона;
![]() – насыпная плотность порошка;
– насыпная плотность порошка;
n – коэффициент, рассчитываемый по формуле:
![]() (4)
(4)
где:
Vпр – объём порошка;
Vсил – объём силикона.
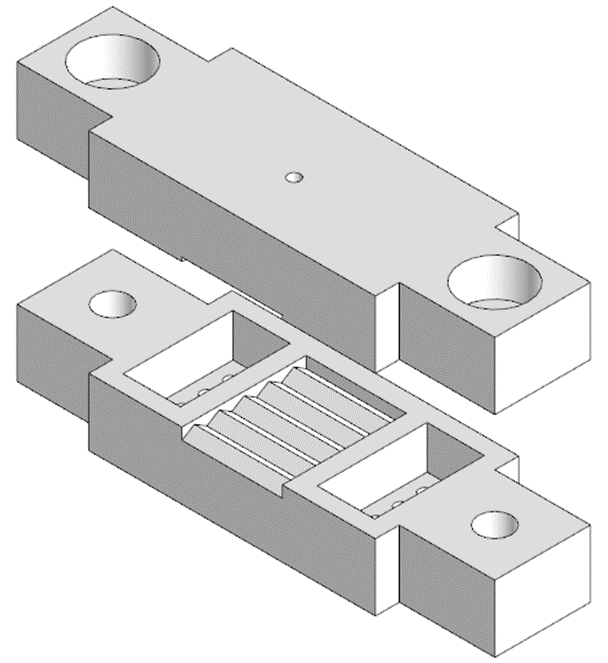
Рис. 3. Зажимы
Для тестовых гибких тензометрических датчиков коэффициент n брался в диапазоне от 1 до 3, так как существовала гипотеза, что объём порошков должен быть равен или больше объёма силикона, а при увеличении объём порошков в более чем 3 раза прогнозировалось существенное ухудшение прочностных характеристик датчика, в том числе размеры зоны упругой деформации.
На первом этапе было изготовлено 6 образцов. Проводя измерение их сопротивления, выяснилось, что при добавлении алюминиевого и медного порошков гибкий тензометрический датчик не проводит электрический ток, в то время при добавлении графитового порошка электрический ток проходит при n равном 3 и не проходит при n равном 1. Из-за этого в дальнейшем опыты проводились только с добавлением графитового порошка.

Рис. 4. Нахождение зависимости сопротивления R от удлинения l при n = 1.0625
Для получения зависимости удлинения от изменения сопротивления были созданы зажимы (рис. 3). Для выявления оптимального коэффициента n применялся метод половинных отрезков. В ходе экспериментов с помощью мультиметра были выявлены коэффициенты n, при которых сохраняются физико-механические свойства и наблюдается проводимость. Из всех тестовых гибких тензометрических датчиков наиболее удачными оказались образцы с коэффициентом n равным 1,125, 1,1875 и 1,0625. Полученные замеры и графики зависимостей представлены в таблицах 1, 2, 3 и рисунках 3, 4, 5. Из полученных зависимостей можно сделать вывод, что наилучшим соотношением силикона с графитовым порошком будет наблюдаться при n = 1.1875.
Таблица 1
Замеры гибкого тензометрического датчика при n = 1.0625
| l | 50 | 56,3 | 61,8 | 66,4 | 71,5 | 75,2 | 81,2 | 85,1 | 91,4 |
| R1 | 2000000 | 34000000 | 211000 | 192000 | 214000 | 340000 | 830000 | 10500000 | 0 |
| R2 | 1800000 | 29000000 | 1260000 | 480000 | 385000 | 690000 | 1145000 | 20000000 | 0 |
| R3 | 1950000 | 32000000 | 1860000 | 380000 | 542000 | 930000 | 1310000 | 1500000 | 0 |
| Rср | 1916666,7 | 31666667 | 1110333 | 350666,7 | 380333,3 | 653333,3 | 1095000 | 10666667 | 0 |
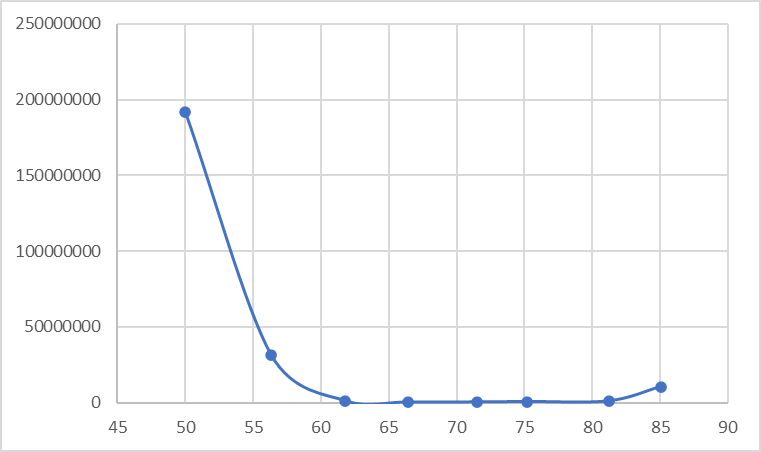
Рис. 5. Зависимость R(l) при n = 1.0625
Таблица 2
Замеры гибкого тензометрического датчика при n = 1.125
| l | 50 | 56,3 | 61,8 | 66,4 | 71,5 | 75,2 | 81,2 | 85,1 | 91,4 |
| R1 | 93930000 | 16343000 | 134000 | 104000 | 121000 | 229000 | 518000 | 5385000 | 0 |
| R2 | 97263000 | 17478000 | 840000 | 231000 | 217000 | 30700 | 709000 | 8072000 | 0 |
| R3 | 103398750 | 14524000 | 1020000 | 226000 | 296000 | 663000 | 78600 | 1216000 | 0 |
| Rср | 98197250 | 16115000 | 664666,7 | 187000 | 211333,3 | 307566,7 | 435200 | 4891000 | 0 |
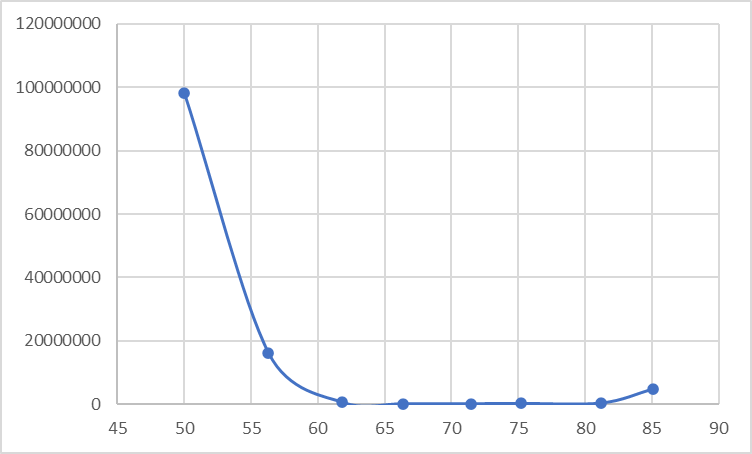
Рис. 6. Зависимость R(l) при n = 1.125
Таблица 3
Замеры гибкого тензометрического датчика при n = 1.1875
| l | 50 | 56,3 | 61,8 | 66,4 | 71,5 | 75,2 | 81,2 | 85,1 | 91,4 |
| R1 | 2000000 | 48800 | 27500 | 27300 | 28600 | 42300 | 112000 | 271500 | 0 |
| R2 | 1800000 | 130000 | 33400 | 40000 | 50000 | 83000 | 157000 | 436000 | 0 |
| R3 | 1950000 | 277000 | 48000 | 40000 | 51000 | 75000 | 133000 | 386000 | 0 |
| Rср | 1916666,7 | 151933,3 | 36300 | 35766,67 | 43200 | 66766,67 | 134000 | 364500 | 0 |
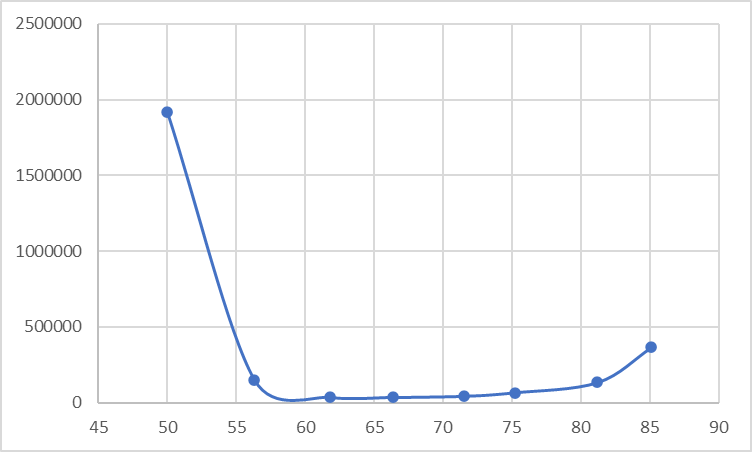
Рис. 7. Зависимость R(l) при n = 1.1875
Из полученных данных можно сделать вывод о несостоятельности математической модели, представленной в статье «Математическая модель для гибких тензодатчиков на основе токопроводящих порошков». Также в ходе тестов были выявлены рабочие диапазон гибкого тензометрического датчика.

.png&w=640&q=75)