Одним из важнейших методов решения задач математической физики является метод конечных элементов. Данный метод моделирует физические явления, включая течение жидкости, теплопередачу, механическую деформацию или распространение электромагнитных волн. Аппроксимация проблемной области в данном методе происходит с помощью конечно-элементных сеток, отсюда и возникает потребность в их построении.
Общая идея генерации сетки заключается в разделении физической области со сложной геометрией на небольшие простые части, называемые элементы, такие как, например, треугольники, четырехугольники, тетраэдры, октаэдры. Может понадобиться генерация миллионов и миллиардов таких элементов. При этом сетка должна удовлетворять следующим требованиям: соответствие геометрии объекта или проблемной области; ограничение на минимальный и максимальный размеры элемента; все элементы должны быть правильной формы, например равносторонние треугольники для двумерной треугольной сетки или равносторонние тетраэдры для трехмерной тетраэдальной сетки. Методы генерации сетки стремятся исключить создание слишком тонких или длинных элементов, например Needle, Cap и Sliver [1, с. 65-78].
В настоящее время преобладают три класса алгоритмов генерации сеток: методы продвижения фронта, в которых элементы генерируются последовательно от границы области к её центру; Overlay grid, quadtree и octree [1, с. 65-78], которые используют вспомогательную структурированную фоновую сетку, используя её как ориентир для разбиения области; различные вариации методов Delaunay Refinement [1, с. 65-78], данные алгоритмы применяются для улучшения качества сеток Делоне путем локальной оптимизации элементов с помощью вставки в триангуляцию дополнительных вершин – вершин Штейнера.
Категория методов улучшения сеток Delaunay Refinements исторически связана с именами исследователей, которые работали в этом направлении. Существует две основных вариации: второй алгоритм Пола Чу [2, с. 404] и алгоритм Рупперта [3, с. 548-485].
Неструктурированные сетки – сетки с произвольным расположением узлов. Состоят такие сетки из ячеек различной формы (преимущественно шестигранники или тетраэдры). Они могут быть сформированы и объединены грань в грань произвольным образом для заполнения любого объёма, например системы охлаждения двигателя [4]. Обычно элементами неструктурированной сетки являются произвольные многоугольники или многогранники.

Рис. 1. Сетка системы охлаждения двигателя
Использование трехмерных триангуляций, в том числе трехмерных триангуляций Делоне, не является оптимальным для получения элементов хорошего качества, в отличие от плоского случая. Однако, данный тип сеток является одним из самых распространенных. Можно обобщить некоторое количество свойств двумерной триангуляции Делоне на трехмерную область, однако большинство свойств оптимальности на трехмерный вариант не обобщаются. Например, трехмерная триангуляция Делоне не максимизирует минимальный угол, а двугранные углы могут быть сколь угодно малы или велики. Обобщим нужные базовые определения на трехмерную область.
Рассмотрим алгоритм Delaunay Refinement. Большую работу в обобщении метода Рупперта на трехмерном пространстве проделал Джонатан Ричард Шевчук [5, с. 97-137], далее в работе будут описан алгоритм, предложенный им.
На вход алгоритма поступает трехмерный кусочно-линейный комплекс P и положительная константа ![]() , которая задает максимально допустимое отношение радиуса описанной сферы к минимальной грани тетраэдра в выходной сетке.
, которая задает максимально допустимое отношение радиуса описанной сферы к минимальной грани тетраэдра в выходной сетке.
Первоочередной задачей алгоритма является восстановление сегментов P, таким образом каждый сегмент является объединением рёбер в ![]() . Вторым приоритетом является восстановление полигонов из P так, чтобы каждый полигон представлял собой объединение треугольников в
. Вторым приоритетом является восстановление полигонов из P так, чтобы каждый полигон представлял собой объединение треугольников в ![]() . Когда сетка соответствует P третьим приоритетом является улучшение качества сетки путем разбиения ее на тетраэдры, чьи отношения радиуса к ребрам не превышают заданной константы
. Когда сетка соответствует P третьим приоритетом является улучшение качества сетки путем разбиения ее на тетраэдры, чьи отношения радиуса к ребрам не превышают заданной константы ![]() . На выходе алгоритм возвращает качественную трехмерную триангуляцию Делоне.
. На выходе алгоритм возвращает качественную трехмерную триангуляцию Делоне.
Введем операции деления ребра, подполигона и низкокачественного тетраэдра.
Определение (Операция деления ребра в трехмерном пространстве)
Пусть трехмерная триангуляция задана своим набором вершин S, набором ребер E, а также заданно ребро ![]() . Чтобы разделить ребро, нужно выполнить следующий алгоритм:
. Чтобы разделить ребро, нужно выполнить следующий алгоритм:
- Вставить середину ребра e в S;
- Удалить из E ребро e, и вставить в E две половины e.
Далее будет описана операция деления подполигона. Подполигоном будем называть треугольник, являющимся частью двумерной триангуляции Делоне на некоторой плоской части кусочно-линейного комплекса P. При этом подполигон, как и ребро, может захватывать некоторую вершину в триангуляции, т. е. внутри минимальной описанной около подполигона сферы лежит некоторая вершина триангуляции.
Определение (Операция деления подполигона)
Пусть трехмерная триангуляция задана своим набором вершин S, набором ребер E, а также задан подполигон ![]() . Чтобы разделить подполигон, нужно выполнить следующий алгоритм:
. Чтобы разделить подполигон, нужно выполнить следующий алгоритм:
- Пусть c – центр описанной около подполигона сферы;
- Если в триангуляции существует ребро
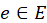 , которое захватывает вершину c, то следует разделить данное ребро. В противном случае следует вставить c в S.
, которое захватывает вершину c, то следует разделить данное ребро. В противном случае следует вставить c в S.
Определение (Операция деления тетраэдра)
Пусть трехмерная триангуляция задана своим набором вершин S, набором ребер E, а также задан тетраэдр t. Чтобы разделить тетраэдр, нужно выполнить следующий алгоритм:
- Пусть c – центр описанной около t сферы;
- Если в триангуляции существует ребро
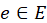 , которое захватывает вершину c, то следует разделить данное ребро;
, которое захватывает вершину c, то следует разделить данное ребро; - Если в триангуляции существует подполигон
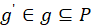 , который захватывает вершину c, то следует разделить данный подполигон;
, который захватывает вершину c, то следует разделить данный подполигон; - Если не были выполнены пункты 2 и 3, то следует вставить c в S.
На рисунке 2 проиллюстрированы вышеуказанные операции деления ребра, подполигона и тетраэдра.
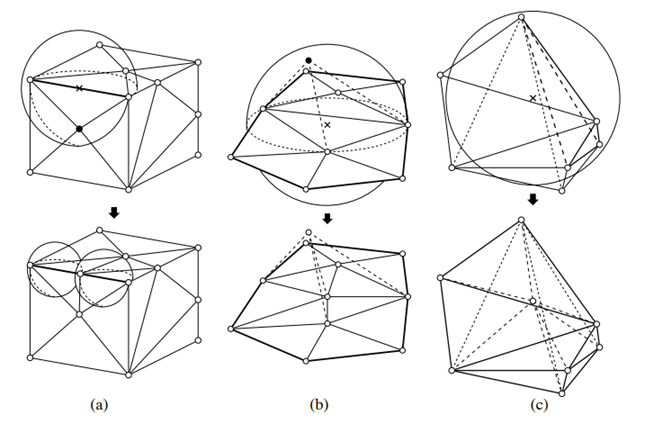
Рис. 2. Иллюстрация вышеуказанных методов. (a) – Деление ребра, (b) – Деление подполигона, (c) – Деление тетраэдра
Определение (алгоритм Delaunay Refinement)
Пусть задан кусочно-линейный комплекс P со своим набором вершин S, набором ребер E, а также задана положительно определенная константа ![]() , определяющая максимально допустимое отношение радиуса описанной около тетраэдра сферы к минимальному ребру. Трехмерная вариация метода Delaunay Refinement, предложенная Джонатаном Ричардом Шевчуком [5, с. 97-137] может быть описана как:
, определяющая максимально допустимое отношение радиуса описанной около тетраэдра сферы к минимальному ребру. Трехмерная вариация метода Delaunay Refinement, предложенная Джонатаном Ричардом Шевчуком [5, с. 97-137] может быть описана как:
- Построить трехмерную триангуляцию Делоне
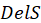 . Для каждого полигона
. Для каждого полигона 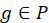 построить двумерную триангуляцию Делоне
построить двумерную триангуляцию Делоне 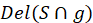 ;
; - Если в триангуляции существует ребро
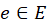 , захватывающее некоторую вершину из триангуляции, следует разделить данное ребро и обновить трехмерную и двумерную триангуляции. Деление производится до тех пор, пока в триангуляции существуют такие рёбра;
, захватывающее некоторую вершину из триангуляции, следует разделить данное ребро и обновить трехмерную и двумерную триангуляции. Деление производится до тех пор, пока в триангуляции существуют такие рёбра; - Если в триангуляции существует подполигон
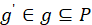 , содержащий захватывающий некоторую вершину из триангуляции и содержащий ортогональную проекцию данной точки, тогда следует разделить данный подполигон и обновить трехмерную и двумерную триангуляции. Деление производится до тех пор, пока в триангуляции существуют такие подполигоны;
, содержащий захватывающий некоторую вершину из триангуляции и содержащий ортогональную проекцию данной точки, тогда следует разделить данный подполигон и обновить трехмерную и двумерную триангуляции. Деление производится до тех пор, пока в триангуляции существуют такие подполигоны; - Если в триангуляции существует тетраэдр
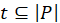 для которого
для которого 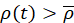 , следует разделить данный тетраэдр и обновить трехмерные и двумерные триангуляции, после этого нужно вернуться к шагу 2;
, следует разделить данный тетраэдр и обновить трехмерные и двумерные триангуляции, после этого нужно вернуться к шагу 2; - Вернуть сетку
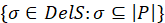 .
.
Рассмотрим пример работы алгоритма на языке С++. Параметры данной тетраэдальной сетки приведены в таблице 1. Для оценки сетки предлагается рассмотреть количество узлов, тетраэдров, длины максимального и минимального сегмента [8, с. 391-393], отношение минимального сегмента тетраэдра к минимальной высоте этого тетраэдра (aspect ratio [6, с. 268]), максимальный и минимальный двугранные углы [6, с. 268], а также гамма-качество элемента по Lo [7, с. 112-127].

Рис. 3. Стартовая низкокачественная сетка
Таблица 1
Параметры стартовой сетки
| Параметр | Значение |
| Количество узлов сетки | 32.0000 |
| Количество тетраэдров | 48.0000 |
| Длина минимального сегмента, м | 0,41758 |
| Длина максимального сегмента, м | 46,45800 |
| Минимальный aspect ratio | 50,43400 |
| Максимальный aspect ratio | 106,72000 |
| Минимальный двугранный угол, град | 0,53713 |
| Максимальный двугранный угол, град | 178,22330 |
| Среднее значение гамма-качества элемента | 0,03301 |
Далее сетка улучшается описанным ранее алгоритмом Delaunay Refinement с параметром ![]() . Результаты видны на рисунке 4 и в таблице 2.
. Результаты видны на рисунке 4 и в таблице 2.

Рис. 4. Улучшенная сетка с параметром ![]()
Таблица 2
Данные об улучшении сетки при ![]()
| Параметр | Значение |
| Количество узлов сетки | 6819.00000 |
| Количество тетраэдров | 21583.00000 |
| Длина минимального сегмента, м | 0,41758 |
| Длина максимального сегмента, м | 2,15620 |
| Минимальный aspect ratio | 1,27880 |
| Максимальный aspect ratio | 18,57600 |
| Минимальный двугранный угол, град. | 5,77290 |
| Максимальный двугранный угол, град. | 164,96240 |
| Среднее значение гамма-качества элемента | 0,72310 |
| Количество точек Штейнера | 6787,00000 |
Приведем некоторые данные об улучшении сеток при вариации параметра ![]() .
.
Таблица 3
Данные об улучшении сетки при различных параметрах ![]()
| Параметр/Коэффициент |
|
|
|
|
| Количество узлов сетки | 6819.00000 | 6923.00000 | 7103.00000 | 7276.00000 |
| Количество тетраэдров | 21583.00000 | 21820.00000 | 22341.00000 | 22935.00000 |
| Длина минимального сегмента, м | 0,41758 | 0,41758 | 0,41758 | 0,30758 |
| Длина максимального сегмента, м | 2,15620 | 2,07760 | 1,92960 | 1,83570 |
| Минимальный aspect ratio | 1,27880 | 1,27880 | 1,27880 | 1,27880 |
| Максимальный aspect ratio | 18,57600 | 15,94900 | 13,27800 | 12,61100 |
| Минимальный двугранный угол, град. | 5,77290 | 5,77290 | 6,20920 | 7,22450 |
| Максимальный двугранный угол, град. | 164,96240 | 164,96240 | 164,96240 | 164,96240 |
| Среднее значение гамма-качества элемента | 0,72310 | 0,72250 | 0,72600 | 0,72790 |
| Количество точек Штейнера | 6787.00000 | 6891.00000 | 7071.00000 | 7244.00000 |
Также рассмотрим гистограмму гамма-качества до и после применения алгоритма.
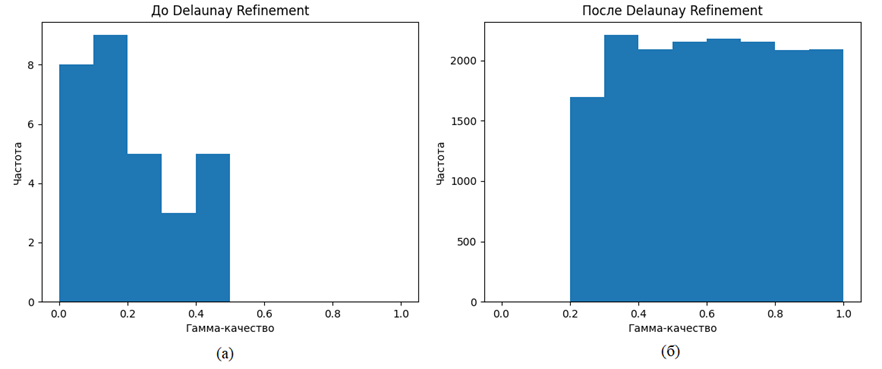
Рис. 5. (а) – гистограмма гамма-качества до применения алгоритма, (б) – после
В результате проделанной работы был изучен метод Delaunay Refinement для генерации неструктурированных тетраэдальных сеток в трехмерном пространстве, изучены преимущества и недостатки метода, а также метод был реализован на языке программирования C++.

.png&w=640&q=75)