О вычислении массы космических тел

Тема предлагаемой статьи, у большинства специалистов, вероятней всего, вызовет недоумение, так как массы всех наблюдаемых космических объектов находятся сегодня из хорошо известного уравнения:

F_цс = F_вд (1)

где:

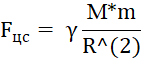– сила гравитационного взаимодействия (центростремительная сила) [2];

γ – гравитационная постоянная;

М – масса гравитационного центра;

m – масса сателлита;

R – расстояние между центрами сателлита и гравитационного центра;

F_вд = m*u_τ² / R – сила вращательного движения;

u_τ – тангенциальная орбитальная скорость.

Откуда масса гравитационного центра равна:

М = (u_τ²*R)/γ (2)

Так для того, чтобы узнать массу Земли нам необходимо знать орбитальную скорость Луны и расстояние между центрами Луны и Земли.

R = 3,845*10⁸ м – расстояние между центрами Земли и Луны.

T = 2,36*10⁶ с – орбитальный период Луны вокруг Земли.

u_τ = 2πR/T = 1023,41 м/с – орбитальная скорость Луны.

γ = 6,6743*10⁻¹¹ м³·кг⁻¹·с⁻² – гравитационная постоянная в Солнечной системе.

M_З = 6,03226*10²⁴ кг – масса Земли.

В настоящее время общепринятое значения массы Земли равно 5,9722*10²⁴ кг. Несмотря на небольшое расхождение в 1%, которое, вероятней всего, связано с уточнением расстояния между центрами Земли и Луны, можно утверждать, что в обоих случаях использовался один и тот же алгоритм расчёта.

Проблема этого расчёта заключается в том, что в качестве центробежной силы на самом деле использовалась тангенциальная сила, направленная по касательной к орбите, в то время как равновесие системы во время вращения обеспечивается именно центростремительной и центробежной силами. Если центростремительная сила вычисляется совершенно, верно, для Солнечной системы по закону «всемирного» тяготения Ньютона, то центробежная сила просто заменена тангенциальной, которая участвует в формировании центробежной силы, но отлична от неё. Именно это отличие и вносит существенную ошибку в современное вычисление масс космических объектов.

Для того, чтобы понять отличие тангенциальной скорости вращательного движения от центробежной необходимо рассмотреть технику метания молота олимпийскими чемпионами, так как вращающийся молот пролетает максимальное расстояние не только от величины скорости его вращения, но и от оптимального угла выхода молота с орбиты вращения. В соответствии с динамикой вращательного движения молот во время вращения перед броском находится под воздействием трех сил:

• тангенциальной, обеспечивающей движение молота по орбите вращения;
• кинематической связи, удерживающей молот на орбите, аналог центростремительной силы при гравитационном взаимодействии;
• центробежной силы, стремящейся перевести вращательное движение молота в прямолинейное.

На рисунке представлен фрагмент броска олимпийского чемпиона по метанию молота Юрия Седых, который в 1986 г. на Чемпионате Европы установил мировой рекорд метания молота 86,74 м не превзойденный до настоящего времени.

Рис. Бросок молота Юрия Седых

Анализ бросков выдающихся спортсменов по метанию молота позволяет с полной уверенностью утверждать, что они используют технику, когда молот уходит с орбиты под углом 54,73561 к касательной орбиты вращения. Это угол прямоугольного треугольника векторов центробежной и тангенциальной скоростей, тангенс которого равен . Таким образом, если тангенциальная скорость вращательного движения равна u_τ, то центробежная скорость при этом равна [1, с. 6-11].

При угле выхода с орбиты молот приобретает линейную скорость равную , что обеспечивает ему максимальную дальность полета. Любой иной угол выхода молота с орбиты снижает его линейную скорость, и соответственно ухудшает результат броска.

Этот же результат расчёта центробежной скорости мы получаем и при векторном анализе вращательного движения:

Отсюда можно сделать вывод, что орбитальное равновесие любого космического тела обеспечивается равенством центростремительной и центробежной силами, поэтому формула (2) для вычисления массы космического тела должна применяться в следующем виде:

(3)

В этом случае масса Земли будет в двое больше принятой на сегодня:

M_З = 12,0645*10²⁴ кг.

Но, тогда, алгоритм вычисления ускорения свободного падения на поверхности космических тел также изменится.

Дело в том, что ускорение свободного падения легко проверяется опытом Ньютона, когда тележку на горизонтальной плоскости передвигает груз при свободном падении с края стола. И это ускорение сегодня измерено с достаточно высокой точностью:

g = 9,80665 м/с²

Ускорение свободного падения связано с гравитационным взаимодействием следующим выражением:

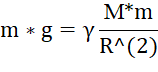(4)

откуда:

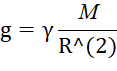(5)

При фактических значениях М=12,0645*10²⁴ кг и g = 9,80665 м/с² расстояние между гравитационным центром Земли и телом на его поверхности равно:

R = (γM/g)^1/2 = 9061457 м

В настоящее время средний радиус Земли установлен в размере 6371300 м. Таким образом, для того чтобы получить наблюдаемое ускорение свободного падения на поверхности Земли её гравитационный центр должен находиться от неё на расстоянии . Но это физически невозможно.

В связи с этим возникает вопрос: как с точки зрения теории устранить противоречие в определении массы Земли, если значение ускорения свободного падения подтверждается реальными наблюдениями движения тел в гравитационном поле Земли?

Как было показано выше, масса Земли определяется из условия орбитального равновесия, и связана со значением центробежной скорости сателлита при его движении по орбите вокруг Земли, игнорировать которую, без нарушения орбитального равновесия нельзя, следовательно, проблема определения ускорения свободного падения связана с ошибкой в определении расстояния между гравитационным центром и телом на поверхности Земли.

В современном расчёте для определения ускорения свободного падения принято значение радиуса Земли. Формула же «всемирного» тяготения исходит из того, что при гравитационном взаимодействие масса гравитационного центра постоянна, и не связана с расстоянием до него. В геоиде это условие не соблюдается, так как его гравитационная масса уменьшается от максимума на поверхности до нуля в центре. Поэтому использование в расчёте радиуса Земли для определения ускорения свободного падения на её поверхности по формуле Ньютона ошибочно.

В связи с этим, при определении ускорения свободного падения на поверхности космического тела при правильном вычислении массы этого тела, с учётом фактической центробежной скорости, необходимо умножать радиус геоида на корень квадратный из 2,02274.

Это связано с тем, что точечный сателлит на поверхности космического тела взаимодействует не со сфероидом, а с конусом, проходящим через ось сфероида с вершиной в точке касания сателлита со сфероидом и основанием, равным диаметру геоида, с противоположной стороны.

Все однородные конусы имеют центр масс на расстоянии ¾H от их вершины. При Н = 2R центр масс конуса находится на расстоянии 1,5R от вершины конуса. Поскольку, большая часть гравитационной массы Земли сосредоточена в её центре, то точка равновесия гравитационного конуса сдвигается к его вершине и находится на расстояние 1,42223R_З от неё.

Именно это значение расстояния между центрами гравитационного взаимодействия на поверхности Земли и надо учитывать при вычислении ускорения свободного падения на поверхности космического тела.

Подводя итог проведенному исследованию следует отметить, что в настоящее время массы всех космических объектов определены с ошибкой связанной с подменой центробежной скорости на тангенциальную в определении их орбитального равновесия.

Сателлит, находясь на поверхности космического тела взаимодействует не с его геометрической формой в виде сфероида, а с его объёмной (виртуальной) проекцией в виде кругового конуса с вершиной в точке касания космического тела с сателлитом и основанием с противоположной стороны диаметром равным диаметру сфероида. Этот феномен можно рассматривать как своеобразную гравитационную голограмму сфероида в ближнем фрагменте гравитационного поля космического тела.

Явление проецирования гравитационной массы сфероидов на виртуальный конус их голографической проекции в настоящее время науке не известно, поэтому этот вопрос требует дополнительной теоретической проработки, чтобы понять механизм перехода от физически реальной формы гравитационной массы к её виртуальной проекции, которую фактически и воспринимает сателлит на её поверхности.