Introduction
The quality of education depends on the quality of a concrete lesson. Therefore, lesson analysis is the most fundamental part of educational quality analysis. The evolution of lesson study and analysis methods reflects a continuous refinement and sophistication over time. Teacher-student interaction and dialogue are the main elements in the classroom. The quality of the teacher's questions directly guides the student's actions and thinking processes in the lesson. Therefore, within the framework of this research, the question is whether it is possible to make a conclusion about the quality of the lesson by analyzing the number and quality of questions asked by the teacher in the lesson. Therefore, lesson analysis is the most fundamental part of educational quality analysis. Teacher-student interaction and dialogue are the main elements in the classroom. The quality of the teacher's questions directly guides the student's actions and thinking processes in the lesson (fig. 1).
Fig. 1. Problem and Question
Education stands as the cornerstone of societal progress, with the quality of teaching and learning experiences serving as the linchpin for effective knowledge dissemination and skill development. In this context, the significance of rigorous research aimed at enhancing educational practices cannot be overstated. This introduction aims to elucidate the critical importance of our research, highlighting significant problems, the current state of the art, gap analysis, novel concepts to fill these gaps, and ultimately, the purpose of our study.
The quality of education is intricately tied to the quality of individual lessons, making lesson analysis a foundational aspect of educational quality assessment (Kayima, 2016). However, there exists a noticeable gap in efforts to explore teachers' questioning practices within Lesson Study contexts, despite the global goal of critically examining and improving teaching practices in such initiatives (Aziza, 2018; Dong, Seah & Clarke, 2015; Larson & Lovelace, 2013; Shahrill & Clarke, 2014; Amirullah, 2018; Lewis, Perry & Hurd, 2009; Lewis, Perry & Hurd, 2004).
Over time, the evolution of lesson study and analysis methods has demonstrated continuous refinement and sophistication (Kayima & Jakobsen, 2020). Central to effective teaching are teacher-student interactions and dialogues, where the quality of the teacher's questions plays a pivotal role in guiding students' actions and thought processes during lessons (Saka & Inaltekin, 2023).
Despite research spanning decades that underscores the critical role of teachers' questions in shaping students' learning experiences, there remains a gap in exploring teachers' questioning practices within Lesson Study contexts (Aziza, 2018; Dong, Seah & Clarke, 2015; Larson & Lovelace, 2013; Shahrill & Clarke, 2014).
Recent studies have explored multidimensional approaches to understanding teacher questioning practices, leveraging technology, mixed-methods strategies, and longitudinal studies (Prakash & Litoriya, 2022). High-level questions have been shown to be beneficial for student learning (Phillips, 2014). In this study, we aim to delve deeper into the results of teacher question analysis presented in previous studies (Saka & Inaltekin, 2023; Kayima & Jakobsen, 2020), synthesizing and critically evaluating these findings to illuminate effective practices that promote active engagement, critical thinking, and meaningful learning in classrooms.
Design and methodology
The research purpose is to develop and test a methodology for studying the level of teachers' questions in regular lessons. The objects of the study include 30 mathematics lesson transcripts, with the subject being teachers’ questions. A coding scheme, utilizing Bloom's Taxonomy, is employed to categorize and classify the level of each teacher's question. Data collection involves a random selection of 30 mathematics lessons from various secondary schools, ensuring a representative sample. Additionally, a classification based on question types is implemented.
Purpose of the research: To develop and test a methodology for studying the level of teachers' questions in a regular lesson.
Objects and subjects of the study:
- Object: 30 mathematics lesson transcript.
- Subject: Teacher’s question.
- Development of Coding Scheme: Utilization of Bloom's Taxonomy to categorize and classify the level of each teacher's question.
Data Collection: Random selection of 30 mathematics lessons from various secondary schools. Collection of verbatim transcripts of the selected lessons, ensuring a representative sample.
Development of Coding Scheme: Utilization of Bloom's Taxonomy to categorize and classify the level of each teacher's question.
Question Types: Additional classification based on question types.
On whether a teacher’s question was relevant or inappropriate, there was a substantial agreement between the 4 analysts, Cronbach's Alpha = 0.887 (95% CI, 0.937), p < 0.0005.
Cronbach's Alpha based on standardized items, with a value of 0.937, further emphasizes the strong internal consistency, suggesting that even when the items are standardized, the reliability remains high.
Research design based on tbla:
- Selection of Lesson Videos: 30 mathematics lesson videos labeled as "Good Lessons" from 2015-2018 are chosen from the ITPD database.
- Transcription of Videos: Verbatim transcripts of all 30 videos are generated, providing a representative sample of lesson content.
- Highlighting Questions in Transcript: Teacher questions are identified using a transcript-based lesson analysis method.
- Determination of Questions Level by Bloom Taxonomy: Four researchers independently categorize questions using Bloom's Taxonomy, ensuring a comprehensive analysis.
- Summarization of Determined Levels: Researchers collaborate to consolidate their categorizations, ensuring a holistic view of question levels.
- Re-Determination of Questions by Bloom Taxonomy: Further refinement of question levels based on collaborative input.
- Data Analysis: The average distribution of questions across Bloom's Taxonomy levels is analyzed for insights into question complexity.
Research Design Based on TBLA Steps:
Step 1. To choose lesson videos
The ITPD has a good lessons database for teachers to use in-service teacher training for all subjects. (2015-2018). We chose 30 math lesson videos.
As for the video lesson selection, 30 videos of “Good Lessons” (Sain khicheel) since 2015 were chosen.
Step 2. To transcript videos into text (fig. 2)

Fig. 2. To transcript videos into text
Table 1
A transcript of the lesson theme “Cone and lateral surface area"
Name of Speaker | Sequential Number | Contents of utterance |
T | 34 | There is a cone. Where is it? |
S | 35 | On the top. |
T | 36 | Yeah, is it on the roof? |
S | 37 | But it is not whole, like a cut. |
T | 38 | Sure, it is not exactly cone. Also what is there? Which shape of door? |
S | 39 | Door is a rectangle. |
T | 40 | How about floor? |
S | 41 | It is a circle. |
S | 42 | Circle |
We did transcript for all 30 video lesson tapes to text on word documents. One hour lesson transcript wroten about 12 pages on A4 format on the word document. You are seeing part of example of a lesson transcript. We wrote it in 3 columns. First column is the name of the speaker, the second one is the number of utterances and the last one is the whole contents of it.
Step 3. To highlight Questions in transcript
The teacher's questions were identified by importing them into a template EXCEL file using a regular transcript-based lesson analysis method (TBLA).
Step 4. To determine Questions level by Bloom Taxonomy (Researchers separately)
Table 2
Questions level
| Questions level | CODE |
| REMEMBER (KNOWLEDGE) | Q1 |
| UNDERSTAND (COMPREHENSION) | Q2 |
| APPLY | Q3 |
| ANALYZE (breaking down into parts, forms) | Q4 |
| EVALUATE (according to some set of criteria, and state why) | Q5 |
| CREATE (SYNTHESIS) | Q6 |
Hand-written notes of Bloom's Taxonomy classification of one lesson by 4 different teachers.
Step 5. To summarize determined levels by 4 researchers
Table 3
Differently defined questions of researchers
| QUESTIONS | teacher | teacher | teacher | teacher |
47 | What is the floor? Q2 | 2 | 3 | 4 | 1 |
51 | There are five-sided and six-sided, right? Q1 | 1 | 3 | 4 | 2 |
| What is the shape of the floor? Q1 | 1 | 3 | 4 | 2 |
78 | Twenty-six and four-tenths square meters. Do the team's answers match? Q4 | 4 | 1 | 5 | 2 |
98 | What about the main tension rope in number two? Q2 | 3 | 4 | 6 | 2 |
| So, did you get an answer from your team here? Q5 | 5 | 4 | 6 | 1 |
100 | Haven't got it yet? Q5 | 5 | 3 | 4 | 2 |
134 | Toono has already entered, so it must not be a cone, right? Q5 | 5 | 4 | 2 | 3 |
| going to cut the cone right? Q5 | 5 | 4 | 3 | 2 |
142 | Since Toono is coming in, what about us here? Q4 | 4 | 2 | 1 | 3 |
167 | It will be a part of Uni, right? Q5 | 5 | 3 | 1 | 2 |
To summarize determined levels by 4 researchers.
Step 6. Re-Determine Questions by level of BT
Table 4 shows the classification of the questions asked by teachers in the 6 -12th grades of mathematics according to Bloom's taxonomy level. Bloom's taxonomy classification of 30 subjects can be seen in table 4 (Appendix 1).
Table 4
Bloom's taxonomy classification of 30 subjects
| Q1 | Q2 | Q3 | Q4 | Q5 | Q6 |
1 LESSON | 18 | 23 | 11 | 14 | 4 | 2 |
2 LESSON | 12 | 14 | 8 | 7 | 3 | 0 |
3 LESSON | 31 | 41 | 33 | 29 | 16 | 9 |
4 LESSON | 24 | 14 | 18 | 17 | 9 | 12 |
5 LESSON | 41 | 73 | 31 | 28 | 32 | 7 |
6 LESSON | 32 | 49 | 51 | 26 | 24 | 9 |
7 LESSON | 9 | 14 | 6 | 0 | 0 | 0 |
8 LESSON | 10 | 9 | 8 | 0 | 0 | 0 |
9 LESSON | 20 | 16 | 32 | 22 | 13 | 5 |
10 LESSON | 16 | 13 | 18 | 4 | 1 | 2 |
11 LESSON | 12 | 11 | 9 | 0 | 2 | 5 |
12 LESSON | 19 | 17 | 15 | 0 | 0 | 0 |
13 LESSON | 14 | 7 | 19 | 0 | 0 | 0 |
14 LESSON | 11 | 8 | 9 | 0 | 2 | 3 |
15 LESSON | 63 | 75 | 61 | 46 | 36 | 6 |
16 LESSON | 105 | 146 | 59 | 35 | 17 | 8 |
17 LESSON | 52 | 68 | 42 | 24 | 32 | 12 |
18 LESSON | 55 | 76 | 54 | 42 | 35 | 7 |
19 LESSON | 46 | 57 | 39 | 25 | 13 | 9 |
20 LESSON | 28 | 17 | 31 | 12 | 14 | 3 |
21 LESSON | 45 | 37 | 34 | 21 | 28 | 5 |
22 LESSON | 31 | 48 | 32 | 35 | 27 | 6 |
23 LESSON | 86 | 57 | 42 | 38 | 45 | 8 |
24 LESSON | 63 | 72 | 29 | 10 | 24 | 7 |
25 LESSON | 31 | 29 | 34 | 24 | 22 | 9 |
26 LESSON | 21 | 19 | 18 | 8 | 19 | 4 |
27 LESSON | 81 | 93 | 78 | 34 | 14 | 8 |
28 LESSON | 16 | 19 | 14 | 1 | 2 | 2 |
29 LESSON | 24 | 39 | 42 | 28 | 19 | 1 |
30 LESSON | 31 | 12 | 16 | 0 | 0 | 3 |
Number of questions asked by the teacher:
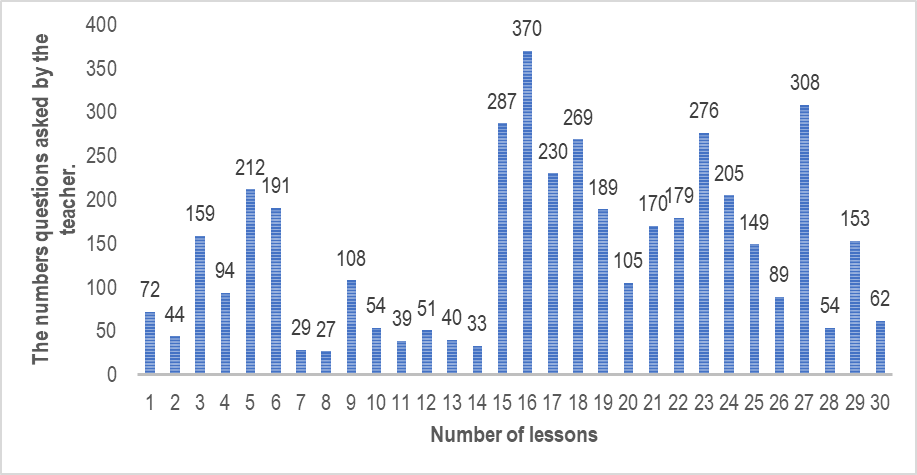
Fig. 3. The numbers questions asked by the teacher
Step 7. To analyze data
Questions levels by Bloom Taxonomy (average).
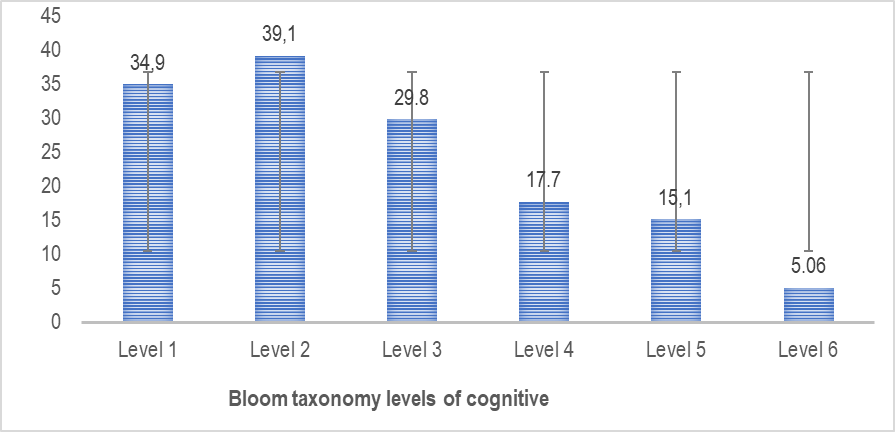
Fig. 4. Questions levels by Bloom Taxonomy (average)
There are more level 1, 2 and 3 questions. On the other hand, fewer level 4, 5 and 6 questions.
Level 1-34.9, Level 2 – 39.1, Level 3 – 29.8, Level 4 – 17.7, Level 5 – 15.1, Level 6- 5.06. The reliability of the research findings is supported by Cronbach's Alpha, indicating substantial agreement among the four analysts. The data reveal a prevalence of level 1, 2, and 3 questions, suggesting a teacher-centered approach with a focus on factual recall. Findings underscore the need for teacher development in the art of questioning, promoting higher-order thinking skills for students. The research highlights the weak questioning abilities of teachers and emphasizes the significance of promoting a diversified range of question types.
The results indicate that the teacher's teaching methods in the analyzed lessons are predominantly teacher-centered.
A call is made for developing the teacher's ability to ask higher-level questions, as it is crucial for engaging students in more meaningful learning activities.
The need for comparative analysis with lessons from other countries is identified for future research.
Findings
We analyzed 30 mathematics lessons using a transcript based lesson analysis approach. In the research, the questions asked by the teacher were classified according to Bloom's taxonomy and question types, and the method of drawing conclusions based on the answers of the students who answered the questions was used.
As you can see from the integrated graph, there are more questions on the Remembering and Understanding levels. In the lessons, the teachers aske Lesson study and lesson analysis methods are becoming more and more sophisticated questions in almost every conversation, and most of the questions were closed or required one or two word answers, as well as low-level questions.
Also, the ability of teachers to ask questions is very weak.
Most of the questions posed by teachers were closed or required brief one or two-word answers. Additionally, a prevalence of low-level questions was observed. This pattern suggests a tendency toward more factual and recall-oriented questioning rather than promoting higher-order thinking skills.
Establish mechanisms for teachers to receive constructive feedback on their questioning techniques. Encouraging self-reflection and peer collaboration can contribute to continuous improvement in instructional practices.
Implications and Recommendations:
- Professional Development for Teachers
- Diversification of Question Types
- Promotion of Higher-Order Thinking
- Feedback and Reflection
- Long-term Comparative Analysis
These findings provide a valuable foundation for targeted interventions aimed at improving the quality and effectiveness of teacher questioning in mathematics lessons, ultimately enhancing the overall learning experience for students.
Discussion
- In order for children to engage in learning activities, they need the ability to ask higher-level questions.
- There is a need to develop the teacher's ability to ask questions.
- In the future, there is a need to compare the lessons of other countries with this methodology.
- The research highlights the significance of promoting a diversified range of question types to enhance the overall learning experience for students.

.png&w=640&q=75)