Подгонки под результат в квантовой механике и математике. Парадоксы вывода соотношения неопределённостей и математических преобразований. Часть 6

Сразу следует отметить, что весь парадокс доказательств в квантовой механике основывается на ошибке, связанной с тем, что наличие предполагаемого закона, например телепортации через потенциальный барьер или соотношения неопределённостей, физики пытаются доказать на основе отсутствия закономерностей через вероятность. Понятно, что доказать наличие закона через его отсутствие из-за случайностей вероятности невозможно. При этом сама вероятность имеет волновой вид, что вероятностному распределению никак не может соответствовать, так как волна это уже закономерность, под закономерность должен быть наблюдаемый физический закон. Разберём суть ошибок таких доказательств. В квантовой механике [1, с. 92] показывается, что если двум физическим величинам соответствуют не коммутирующие друг с другом операторы, то в рамках квантовой механики они не могут быть одновременно измерены точно. Наиболее важным в этом отношении является вычисление отклонения от средних значений операторов двух канонически сопряжённых величин: координаты х и импульса р_х. При этом ограничиваются рассмотрением случая, когда волновая функция Ψ=Aexp[(-i/ћ)(Et-pr)] носит вероятностный характер [1, с. 88] и не зависит от времени (стационарный случай). Это связано с тем, что атом должен излучать кванты фотонов, что определяет необходимость дискретности, а это требует неизменности во времени между уровнями энергетических состояний атома. Причём по постулатам Бора атом в таком состоянии не может излучать. Отметим, что комплексно сопряжённая величина волновой функции определяется в виде: Ψ*=Aexp[(i/ћ)(Et-pr)] в полярной системе координат на основании формул Эйлера. Средние значения координаты и импульса находятся из соотношений:

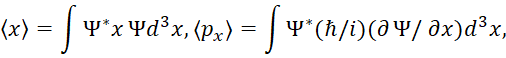(1)

При этом отмечается, что средняя ошибка, или отклонение от среднего, вычисляется по формуле:

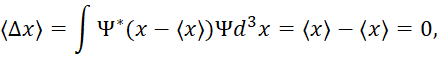(2)

и равна нулю. Однако, это всё же никоим образом не означает отсутствия других возможных положений частицы отличных от , поскольку отклонения могут иметь относительно центра тяжести различные знаки и, следовательно, в среднем взаимно компенсировать друг друга.

Поэтому отклонение от среднего значения следует характеризовать средней квадратичной ошибкой, которая при любом отклонении от имеет положительный знак. Эта средняя квадратичная ошибка для координаты (дисперсия) может быть вычислена по формуле:

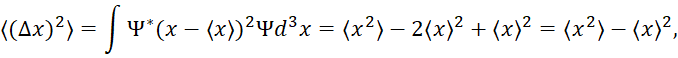(3)

Обращение в нуль средней квадратичной ошибки, например, , означает, что вероятность пребывания электрона в пространстве отлична от нуля лишь при . В этом случае среднее значение равняется точному, то есть, соответствующая вероятность пребывания частицы в точке х описывается δ-образной функцией (функция, стремящаяся к бесконечности в конкретном местоположении).

Аналогично для средней квадратичной ошибки по импульсу имеем:

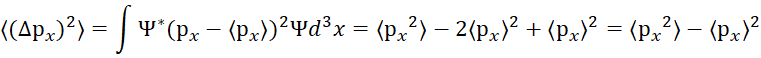(4)

Чтобы установить связь между и , мы можем, без ограничения общности доказательства, выбрать систему координат с началом в центре тяжести волнового пакета (), причём выбрать её так, что она движется вместе с последним (). Собственно, тут уже кроется первая ошибка по соотношению неопределённостей, которую в квантовой механике пытаются вывести математически. Это связано с тем, что чем точнее известны параметры расположения частицы по х, тем значение импульса р_х должно быть менее определённым. Но физиков и математиков это не смутило, и они получили:

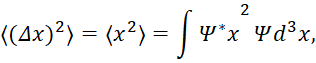
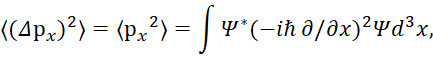(5)

А вот дальше физики и математики предлагают рассмотреть следующий интеграл:

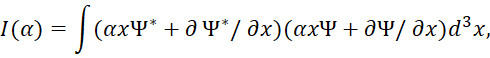(6)

где – некоторая произвольная вещественная величина, не зависящая от х.

Следует отметить, что это в математике можно взять для рассмотрения любой интеграл, для доказательств математических преобразований, а в физике этот интеграл должен соответствовать реальному физическому процессу. А этого как раз нет, так как волновые функции Ψ, которые изначально связаны с вероятностью, не могут соответствовать ни одному физическому закону, так как исключают детерминированную связь. Собственно, на наличии ошибки, связанной с отсутствием связи математических преобразований с физическими законами и получено доказательство гипотезы Пуанкаре, сделанное Григорием Перельманом для трёхмерного измерения. В физике для связи объектов (замкнутости) требуется четырёхмерное измерение на основании преобразований Лоренца-Минковского.

Далее это выражение (6), придуманное физиками и математиками, представляется в виде (фактически квадратное уравнение):

(7)

Для значения А имеем:

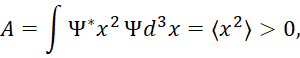(8)

Для значения В следует формула:

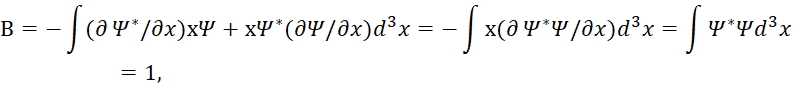(9)

Для значения С следует формула:

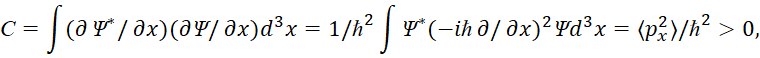(10)

В формуле (10) для перехода к дисперсии импульса использовался как бы эквивалентный переход математического преобразования с учётом экспоненциального вида волновых функций, при котором дифференцирование не изменяет вида самой функции. Понятно, что в формуле (9) значение B=1 не соответствует самим математическим преобразованиям при дифференцировании по х. Действительно, если учесть комплексно-сопряжённый вид волновых функций с учётом аналогичных преобразований, показанных в [1, с. 33], то имеем:

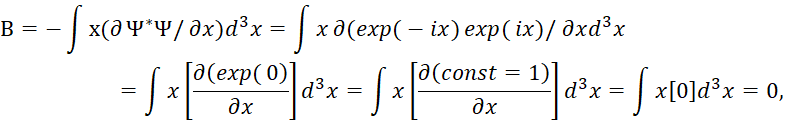(11)

То есть подстановка конкретных значений волновых функций Ψ явно не соответствует значению в формуле (9). Аналогичную ситуацию при подстановке комплексно-сопряжённых функций мы наблюдаем и для формулы (10):

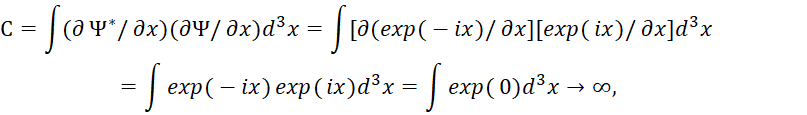(12)

То есть, отсутствие изменения вида функции при дифференцировании, которое использовалось в (10) для нахождения, дисперсии импульса при подстановке конкретных функций даёт иной результат, чем это считается в (10). Однако данные подгонки под результат не смутили физиков и математиков, и они посчитали, что, так как подынтегральное выражение в (6) – положительная величина или ноль, то:

(13)

А вот дальше уже чисто из математики получают условия для ограничения на коэффициенты А, В, С. На сколько это не очевидно, можно понять, если учесть, что в математике чисто арифметически 5-5=0, в физике условия компенсации просто быть не может, так как это означает превращение некоторого количества объектов в ноль (ничто). Реально в физике происходит преобразование объектов из волнового вида в корпускулярный вид и наоборот. Именно поэтому аннигиляция электрона и позитрона даёт фотоны, а столкновение фотона с препятствием даёт пару электрона и позитрона. Надо отметить также, что при интерференции электромагнитных волн также не происходит компенсации и волна имеет дальнейшее распространение, а это говорит о взаимодействии с пространством и временем на основании принципа Гюйгенса-Френеля с переходом в момент компенсации в корпускулярный вид.

Далее физиками и математиками считается, что соотношение (13) будет иметь место для любых вещественных значений , если оно выполняется при , отвечающих минимуму функции . Значение может быть найдено из условия:

(14)

Поэтому минимальное значение равно:

(15)

Иными словами доказательство необходимости соотношения неопределённости сводится к решению квадратного уравнения (7). Отсюда следует, что неравенство (13) имеет место для любых вещественных значений , если выполняется условие:

(16)

Соответственно подставляя значения для А, В, С из (8), (9) и (10) и принимая во внимание (5), находят соотношения между и :

(17)

Это неравенство и представляет собой формулировку соотношения неопределённостей Гейзенберга.

Таким образом, суть доказательства свелась к тому, что, выбрав некоторую математическую функцию вида (6), создали новую зависимость между дисперсиями координаты и импульса, которая не подтверждается физическим законом, а далее на основании этой новой зависимости получили соотношение неопределённостей между координатой частицы и её импульсом. Явная подгонка под результат!

Далее в квантовой механике рассматривается доказательство не коммутативности операторов р_х и х на основании следующих соотношений:

(18)

Отсюда следует:

(19)

Понятно, что значение x в данном случае рассматривается в качестве линейно изменяющейся величины, а оператор импульса р_х отображает действие по изменению по координате х, что характеризуется операцией дифференцирования. В операторной форме получаем:

(20)

Однако вид формулы (20), мягко говоря, не точен, так как из него произвольно исключили волновую функцию Ψ, хотя действие оператора р_х основано на воздействии на волновую функцию Ψ, а иначе запись лишена физического смысла наличия самого оператора, и это сделано не случайно, так как далее записывается соотношение:

(21)

Отсюда видно, что исключение волновой функции Ψ (а это не допустимо, что заставило Шрёдингера в своём уравнении (34) умножить потенциальную энергию V на волновую функцию Ψ [1, с. 36]) позволило заменить значение постоянной Планка в формуле (17) на разность по формуле (20). Однако данное тождество не означает по физике связывающий закон, так как нет практически наблюдаемых аналогов.

Таким образом, в формуле (21) совместили вместе две подгонки под результат и сделали вывод, что если два оператора М₁ и М₂ не коммутируют друг с другом, то для них всегда имеет место соотношение неопределённостей:

(22)

При этом имеем:

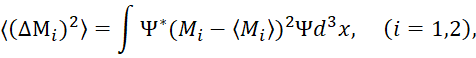(23)

На основании этой подгонки под результат делается вывод, что соотношение неопределённостей является следствием корпускулярно-волнового дуализма, лежащего в основе квантовой механики, и не связано с субъективной стороной опыта, т. е. с наблюдением. Фактически физики закону корпускулярно-волнового дуализма через наличие противоположностей в одном объекте (без противоположностей нет взаимодействия и нет различий) приписали требование наличия чудес по соотношению неопределённостей на основе подгонок под результат!

Смысл соотношения неопределённостей по мнению физиков заключается в том, что распределения плотности по переменным, которым соответствуют не коммутирующие операторы, принципиально не могут одновременно иметь вид δ-функций (рис.).

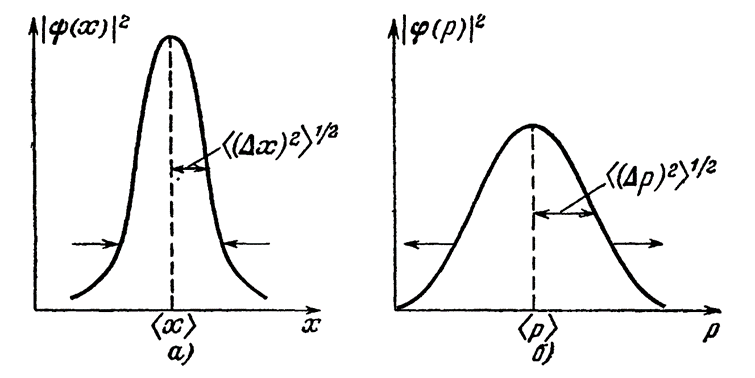
Рис. Распределение плотности вероятности в координатном (а) и импульсном (б) пространствах

При этом, чем ближе к δ-функции распределение вероятности по одной переменной, тем более размытым становится это распределение по другой. В пределе, когда, например, распределение по х, т. е. |Ψ(х)|², примет вид δ-функции [], по импульсу р_х оно станет таким, что для всех значений р_х величина |φ(р_х)|² будет постоянной, т. е. []. Соответственно это даёт парадокс, так как величина импульса непосредственно определяет следующее положение частицы в пространстве, а это означает, что точной координаты местоположения тоже быть не может, так как значение импульса непосредственно определяется по изменению в пространстве.

Таким образом, мы видим, что при соотношении неопределённостей исключается закон физики, при котором значение импульса может быть найдено от величины изменения местоположения частицы в пространстве в соответствии со вторым законом Ньютона. А это означает возможность телепортации, и тогда возможны любые чудеса. Однако элементарная частица в камере Вильсона имеет однозначную траекторию движения, и здесь нет места соотношению неопределённостей. То есть, первоначальный выбор соотношения (6) связи дисперсий координаты и импульса уже изначально не верен. Соответственно вывод о том, что некоммутируемые операторы должны иметь закон соотношения неопределённостей также, не соответствует действительности. Понятно, что парадокс несоблюдения при соотношении неопределённостей второго закона Ньютона:

(24)

видели и физики. Поэтому для доказательства соблюдения выражения (24) ввели классические и квантовые скобки Пуассона [1, с. 95]. Как это будет видно ниже, отсюда вывели некоторые соотношения перехода от движения элементарной частицы в микромире на основе соотношения неопределённостей к движению в макромире по классическим уравнениям. Суть данного подхода основывается на том, что состояние системы в классической механике определяется так называемыми динамическими переменными. Эти величины для системы, заданной функцией Гамильтона , зависят, как правило, от координат х_i, импульсов p_i, и времени t, т.е. f=f((х_i,p_i,t). При этом х_i, и p_i подчиняются каноническим уравнениям Гамильтона:

(25)

Из (25) мы видим, что в данном случае есть однозначная связь импульса и координаты без зависимости соотношения неопределённостей. А вот дальше вводятся так называемые классические скобки Пуассона, где изменение величины f со временем в силу уравнений (25) определяют равенством:

(26)

Здесь:

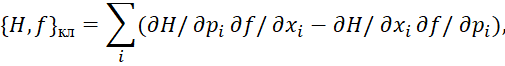(27)

получило название классических скобок Пуассона.

Сразу можно заметить, что в уравнении (26), как слева, так и справа от знака равенства стоит одна и та же величина и по правилам математики мы должны иметь уравнение для классических скобок Пуассона при сокращении на одинаковый член в виде:

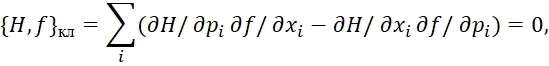(28)

С учётом рассмотрения процессов по одной координате по геометрии Эвклида, а это допустимо в силу того, что по классике есть однозначная связь между импульсом и силой, мы будем иметь:

(29)

Такой вариант равенства возможен только в том случае, если f=H. Конечно, такая запись математически возможна, но она не несёт в себе информации о получении при этом новых законов физики, связывающих импульс р_х и координату х на которые можно было бы в дальнейшем опираться. Надо отметить, что введение величины в обе части от знака равенства уравнения (26) сделано не случайно, а для совпадения с формулой (40) для квантовых скобок Пуассона.

Далее физиками делается вывод, что если f не зависит явно от t, то и поэтому её изменение будет полностью определяться скобками Пуассона:

(30)

Иными словами, если справа от знака равенства в (26) , то слева от знака равенства она не должна равняться нулю. Как это с точки зрения математики может быть? Это возможно только с точки зрения физики по нашей теории, когда слева и справа от знака равенства рассматривается один и тот же объект с точки зрения противоположностей (равенство в одной противоположности означает неравенство в другой противоположности), но не для случая данного математического равенства при рассмотрении процессов в одной противоположности. При обращении производных по времени в ноль ({H,f}_кл=0) величина f не должна зависеть от времени, то есть будет сохраняться:

(31)

Например, если энергия явно от времени не зависит, то и в силу очевидного равенства {H, Н}_кл=0 мы найдём, что функция Гамильтона (т.е. в данном случае энергия) является величиной постоянной (Н=const). В принципе, как мы показали выше, данное умозаключение уже следовало из формулы (26) при сокращении на одинаковый член в правой и левой части уравнения. Понятно, что в случае подстановки в уравнение (28) при ({H,f}_кл=0) вместо f координаты x_i, мы получим:

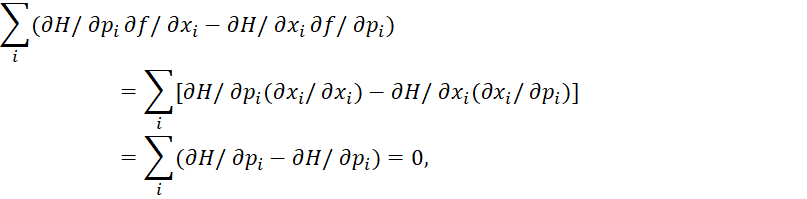(32)

Аналогичный результат будет при f=р_i:

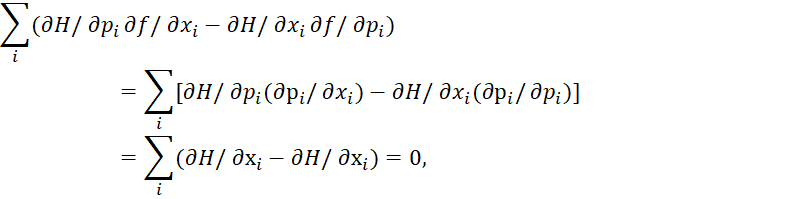(33)

Соответственно нас удивляет вывод физиков в квантовой механике, что подстановки f=р_i, и f=х_i на основе классических скобок Пуассона дают канонические уравнения Гамильтона, когда этот вариант уже получен для функции Гамильтона по уравнениям (25). В классике законов физики не может быть двузначного получения величин по разным формулам, так как это отрицает наличие необходимости самих законов.

Понятно, что сама математическая конструкция классических скобок Пуассона лишена логического смысла, так как нет физических законов, которые доказывали бы необходимость такого математического преобразования.

Если предположить вариант вида (30) при , то классические скобки Пуассона дают вариант, соответствующий нулю, как это показано выше. Иными словами, остаётся вариант, который соответствует нестационарным процессам с изменением энергии во времени. Однако этот вариант нестационарных процессов в квантовой механике не рассматривается при использовании уравнения Шредингера, так как определяются дискретные уровни энергии в атоме с устоявшимися значениями волновых функций, которые определяют вероятность местонахождения частицы. Действительно, можно с помощью уравнений Шредингера описать два различных дискретных состояния частицы, но для перехода с одного уровня на другой во времени надо иметь законы изменения состояния, а их в квантовой механике просто быть не может в силу отрицания самих законов через вероятность неопределённости. Так стационарное уравнение Шредингера, когда потенциальная энергия не зависит от времени, имеет вид:

(34)

Соответственно мы имеем дискретные уровни энергии Е_n не зависящие от времени, которые определяют значение (f) без изменения во времени.

Понятно, что, чтобы получить изменение значения f во времени должно быть введено изменение потенциальной энергии во времени в виде V(r,t), но тогда волновые функции Ψ также становятся зависимыми от времени. При этом всякое изменение во времени даёт либо излучение, либо поглощение фотонов, при этом такой квант энергии необходимо учитывать в уравнении. Напомним, что по постулатам Бора в атоме нет причин для излучения, а значит и поглощения.

Так как физики и математики в квантовой механике считают, что физический смысл имеют только средние значения операторов (координаты, импульса и т. д.) то они ищут изменение со временем.

В общем случае среднее значение произвольного оператора М даётся в квантовой механике формулой:

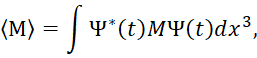(35)

При этом время t входит в произвольный оператор как параметр. Учитывая данную формулу, находят полую производную по времени в виде:

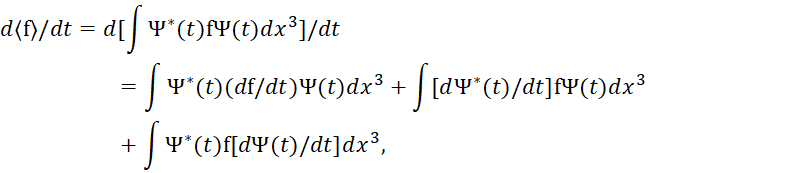(36)

Однако мы видим, что виду (35) соответствует только член 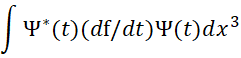, а два других члена возникли из-за того, что дифференцирование во времени было применено не к оператору f для нахождения усреднённого значения производной, а ко всему интегралу. То есть, здесь, как бы рассматриваются различные значения усреднения самого оператора f, а не его производной по времени. И в данном случае вероятность становится зависимой от времени, но как это может быть, и на основании какого закона не поясняется. Для этого введены добавочно зависимости от производных по времени волновых функций, характеризующих вероятность, что не соответствует (35).

Далее, исходя из того, что мы имеем зависимости по уравнениям Шредингера [1, с. 100] вида:

(37)

в уравнении (36) делается соответствующая замена, и мы имеем вид:

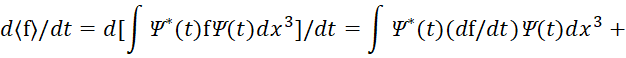
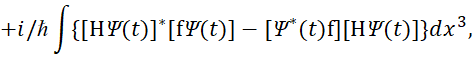
(38)

Так как оператор Н является вещественным, а значит самосопряжённым, то верна запись:

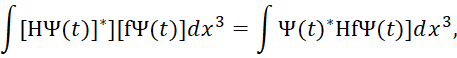(39)

Однако такое действие явно расходится с физическим смыслом и логикой, так как оператор Н в (38) применялся к значению волновой функции , а в (39) он применяется к произведению , а это уже совершенно другая физическая величина. Соответственно отсюда получается формула:

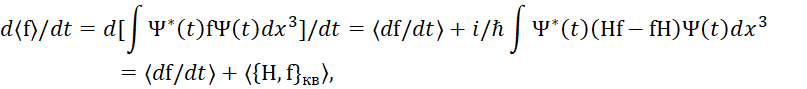(40)

Здесь выражение:

(41)

по мнению физиков, представляет собой обобщение классических скобок Пуассона (27) на квантовый случай и поэтому носит название квантовых скобок Пуассона, а связанная с ними величина:

(42)

Называется коммутатором операторов H и f.

Следует отметить, что выражение: фактически аналогична выражениям (18) и (19) для операторов х и р, и оно равняется нулю, если f не зависит от оператора H. Кроме того, мы видим, что формула (40) аналогична формуле (26), а так как , в силу того, что время это детерминированная величина и усреднение касается только оператора f, то мы имеем аналогию с классическими скобками Пуассона:

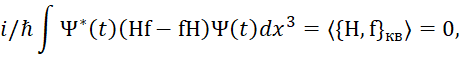(43)

А это означает, что оператор f не зависит от оператора Н. Собственно, данный результат рассматривается и в квантовой механике, где энергия должна сохраняться для частицы, движущейся в потенциальном поле V(r), которое не зависит от времени. В этом случае имеем выражение:

(44)

То есть, . С другой стороны, согласно стационарному уравнению Шредингера (34), когда есть условие:

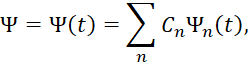(45)

мы имеем для значения величину энергии:

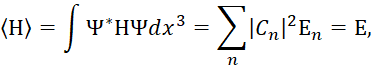(46)

Таким образом, уравнение (46) представляет собой не что иное, как закон сохранения энергии (Е=const) для частицы, движущейся в силовом поле, не зависящим от времени.

Следовательно, мы видим, что искусственно введённые математические конструкции скобок Пуассона не дают новых выражений в использовании функции Гамильтона за счёт использования зависящего от времени оператора f, и результат вновь сводится к стационарному случаю. При этом выражение, как в классических скобках Пуассона, так и в квантовых скобках даёт ноль, что мы показали выше. Однако игнорирование равенства членов df/dt в уравнении (26) и членов в уравнении (40) слева и справа от знака равенства далее используется в теореме Эренфеста [1, с. 100]. Здесь ищется квантовый аналог классических уравнений движения (25), но с использованием квантовых скобок Пуассона вместо уравнения Гамильтона. Понятно, что данный подход означал бы неоднозначность законов физики за счёт статистического усреднения. Но это не остановило физиков и математиков, и они, замечая, что операторы х и р_х не содержат времени явно, воспользовались для определения производных соотношением:

(47)

При этом физики предполагают в нём соответственно f=x и f=p_x.

В случае f=x находят:

(48)

Далее учитывается коммутативность х и V(x), и формула (48) приводится к виду:

(49)

Соответственно мы показывали в (32), что при f=x для классических скобок Пуассона равенство выражения нулю. В случае квантовых скобок Пуассона мы имеем расхождение с результатом от классических скобок Пуассона на основании формул (18) и (19), что далее и используется. С этой целью в правую часть выражения (49) добавляется величина (р_ххр_х-р_ххр_х), равная нулю, и отсюда имеют:

(50)

Далее принимается во внимание формула (20), которая используется в соотношении неопределённостей Гейзенберга. В итоге получают:

(51)

Аналогично для определения изменения импульса со временем, мы должны в формулу (47) вместо оператора f подставить оператор импульса р_х. Тогда, замечая, что р_х р_х²-р_х² р_х=0, находим:

(52)

В силу того, что , а . Отсюда с учётом второй производной от (51) получают:

(53)

В уравнениях (51) и (53) нет ничего противоречащего законам физики. Однако парадокс в том, что в теореме Эренфеста, при получении средних значений движения частицы, была использована формула (20), а именно её связывают по формуле (21) с соотношением неопределённостей Гейзенберга. Кроме того, в классической теории значение скорости и силы находят по формулам в (25). Поэтому, если искать средние значения, то это надо за счёт оператора Гамильтона с учётом его дифференцирования по координате и импульсу, а в теореме Эренфеста это делается через формулу (47) с подстановкой операторов координаты и импульса и отсутствием коммутативности, что должно давать ноль по классике по формулам (32) и (33). Понятно, что вероятностное усреднение изначальных нулевых значений по классике (32) и (33) не может дать иное значение, чем ноль. Соответственно, по физике не может быть неоднозначности закона при получении физических величин, так как это означает чудо неопределённости самого закона. И это ещё раз подтверждает подгонку под результат в квантовой механике за счёт искусственных математических конструкций. Соответственно у физиков, на основе этих новых математических конструкций, возникла необходимость перехода от квантовых уравнений движения к классическим уравнениям для обоснования необходимости неопределённости между координатой и импульсом [1, с. 101]. С этой целью предлагается сравнить формулу (24) с соответствующей формулой (53). При этом учитывается, что роль классической координаты в квантовой теории играет величина . Поэтому с учётом детерминированности законов физики квантовое уравнение должно совпадать с классическим уравнением, если бы вместо (53) имели:

(54)

т. е., если бы в классическое соотношение между силой и координатой было подставлено вместо х его среднее значение . Однако согласно теореме Эренфеста в уравнения движения в квантовом случае входит среднее значение самой силы, т. е. (закон физики стал неоднозначным, так как сила перестала зависеть от координаты). Отсюда делается вывод: чтобы перейти от квантовых уравнений движения к классическим уравнениям, следует установить связь между величинами и . С этой целью представляют оператор силы в виде:

(55)

где . Далее предлагается разложить в ряд Тейлора вблизи точки . Тогда получаем:

(56)

Произведя усреднение этого выражения по формуле (35) и принимая во внимание, что , получаем:

(57)

Вот тут надо отметить, что, исключив приращение по первой производной силы, мы нарушили закон однозначной связи силы и координаты в зависимости от потенциальной энергии, то есть изменили сам физический закон, когда есть зависимость силы и от приращения . Иными словами, в усреднении силы отсутствует зависимость от направления движения. Это исключает силу как векторную величину. Соответственно все нечётные значения степени в ряде Тейлора также должны равняться нулю. С точки зрения математики усреднение заменяется дисперсией. Отсюда получают, что есть зависимость:

(58)

Иными словами, возникает некая квантовая поправка к классическому уравнению Ньютона, дающая неопределённость закона физики между силой и координатой нахождения частицы при наличии потенциальной энергии. Отсюда, критерием перехода квантовых уравнений движения в классические уравнения является неравенство:

(59)

Далее замечается, что выполнение этого условия ещё не означает возможности применимости всех классических понятий для описания движения микрочастицы. В самом деле, в квантовой механике среднее значение кинетической энергии , по аналогии с формулой (58), определяется выражением:

(60)

где , .

Одновременно классическим аналогом кинетической энергии считают величину:

(61)

Отсюда следует условие перехода от квантового выражения кинетической энергии (60) к классическому выражению (61) в виде:

(62)

Иными словами, физики также утвердили отсутствие закона необходимости однозначной связи кинетической энергии и импульса! Ну и чтобы получить возможность использования классического приближения в микромире умножили неравенство (62) на (59):

(63)

Если к тому же учесть ещё соотношение неопределённостей (17), то последнее условие принимает вид:

(64)

Таким образом, мы видим, что подгонки под результат с получением неопределённостей в законах физики в микромире были связаны с допущением математических конструкций, противоречащих элементарной логике. Это соответственно, как бы оправдывало чудеса наличия нулевой энергии и телепортаций, которые мы раскрыли в [2, с. 12-32; 3, с. 5-26; 4, с. 6-21; 5, с. 9-34; 6, с. 18-40]. Понятно, что студенты физико-математических факультетов не способны выявить парадоксы таких подходов в силу отсутствия полноты знаний и исходя из доверия к авторитетам. Отсюда из университетов выходят специалисты не способные логически мыслить и изобретать. Понятно, что преподаватели не заинтересованы в рассмотрении теории мироздания от простого к сложному с объяснением законов физики на основе элементарной логики, что мы показывали не раз в [7, с. 10-24; 8, с. 40-56; 9, с. 32-58; 10, с. 3-23; 11, с. 15-30; 12, с. 5-28; 13]. Именно поэтому мы продолжаем вскрывать подгонки под результат последовательно и методично. Современные академики РАН пытаются привязать успехи в получении атомного оружия, лазеров и работу полупроводников к наличию правильных подходов в квантовой механике. Однако, когда начинаешь детально разбираться в наличии совпадения практических результатов с теоретическими результатами квантовой механики, то кроме методов подгонки под результат с наличием чудес телепортации в квантовой механике ничего нет. Мы этому раскрытию парадоксов посвятили не один десяток научных публикаций.