Для того, чтобы правильно понять данную статью, а также для понимания поднятой здесь темы, следует для начала разобраться:
- Что такое электрический фильтр?
- Что такое ARC-фильтр?
- Чем полосовой фильтр отличается от других видов?
Пойдем по порядку. Электрический фильтр – это четырёхполюсник, который пропускает один диапазон частот, который мы хотим оставить неизменным, и заглушает другой диапазон, который не требуется в результате.
ARC-фильтр или по-другому активный – это электрический фильтр в конструкции которого присутствует один или несколько реактивных элементы, например: транзистор или операционный усилитель.
Наиболее частыми в использовании являются фильтры: нижних частот, верхних частот и полосовые фильтры. Фильтр нижних частот – фильтр, пропускающий частотный спектр сигнала ниже некоторый частоты и заглушающий частоты выше. Фильтр верхних частот наоборот, пропускает верхние частоты и заглушает частоты ниже заданной. Полосовой фильтр является неким «гибридом» фильтра нижних и верхних частот, так как он пропускает только определенную полосу частот и заглушающий все частоты выше и ниже полосы пропускания
Любой полосовой фильтр имеет несколько основных параметров, определяющих его характеристики:
- Полоса пропускания (полоса с наименьшим затуханием сигнала, при проходе через фильтр)
- Полоса затухания (полоса, в которой сигналы максимально возможно ослабляются)
- Коэффициент усиления (параметр, показывающий во сколько раз сигнал будет усилен или ослаблен в полосе пропускания).
Принцип работы полосового ARC-фильтра основан на изменении коэффициента усиления в зависимости от частоты входного сигнала. Основной в фильтре является RC-цепочка, включенная в цепь обратной связи, которая при изменении частоты влияет на коэффициент усиления.
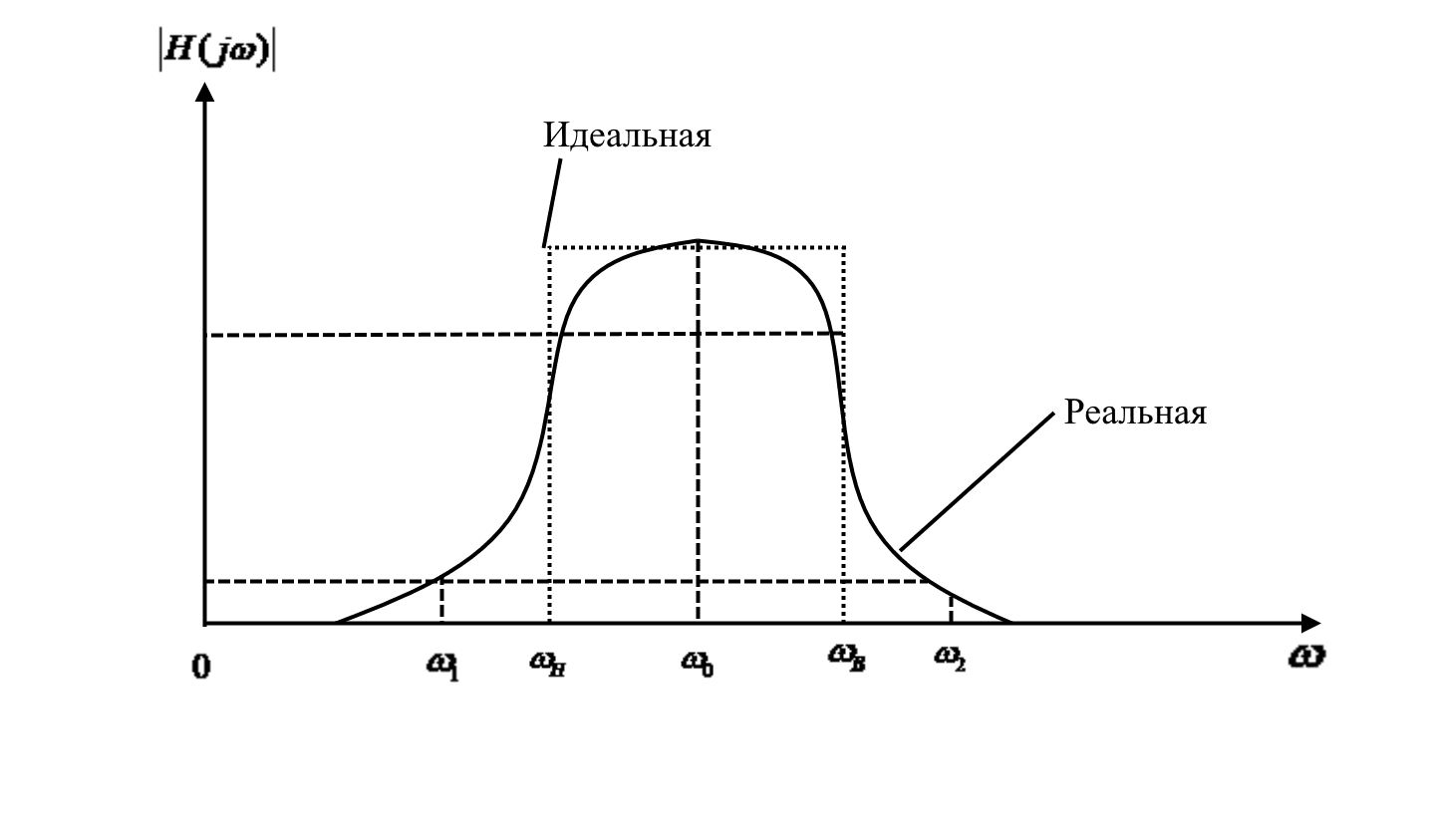
Рис. 1. АЧХ полосового фильтра
На рис. 1 представлена модель амплитудно-частотной характеристики активного полосового фильтра.
Разобравшись в теоретических нюансах работы активного полосового фильтра, можно перейти к расчетам элементов, входящих в состав фильтра.
Исходные данные
За исходные данные были взяты два конденсатора с одинаковыми ёмкостями С=С1=С2=3300 пФ, частота квазирезонанса (это центральная частота RC фильтра, не являющегося резонансной цепью) была взята равной fx=2633 Гц, так как именно эта частота позволяет получить более качественную амплитудно-частотную характеристику. За входное напряжение был взят стандартный аккумулятор, разность потенциалов на концах которого равно U=5 В.
Далее требовалось выбрать добротность нашего контура, а также коэффициент усиления фильтра. Для выбора было использовано условие, что коэффициент усиления (К) должен быть меньше двух квадратов добротности (Q) контура, то есть: K<2⋅Q2. Исходя из условия мы получили, что добротность контура равна Q=40, а коэффициент усиления K=220 дБ.
Следующим этапом было рассчитать резистивные элементы. В состав нашего фильтра входит пять резистивных элементов, которые требуется рассчитать, учитывая исходные данные, выбранные выше.
Первым, что требовалось сделать, это рассчитать циклическую частоту квазирезонанса:
ω0=2πfx=2π⋅2633=16500 рад/с
Далее нам достаточно данных, чтобы произвести расчет первых трех резисторов
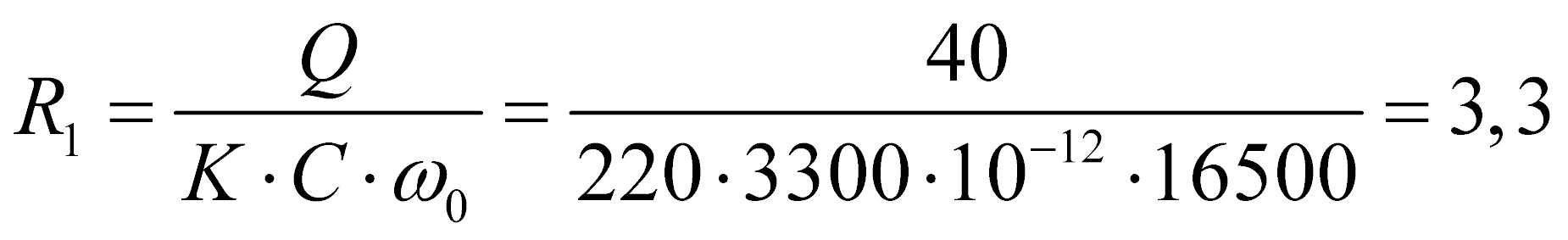 кОм
кОм
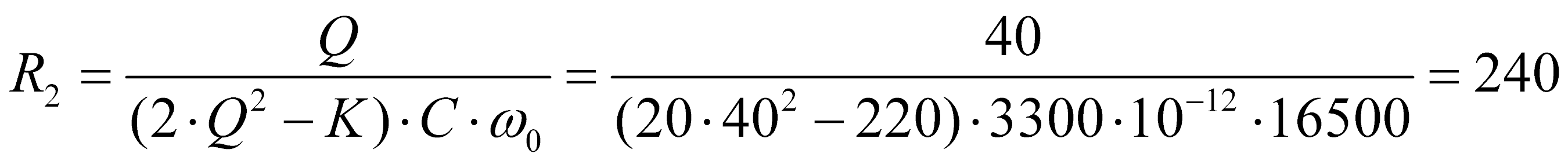 Ом
Ом
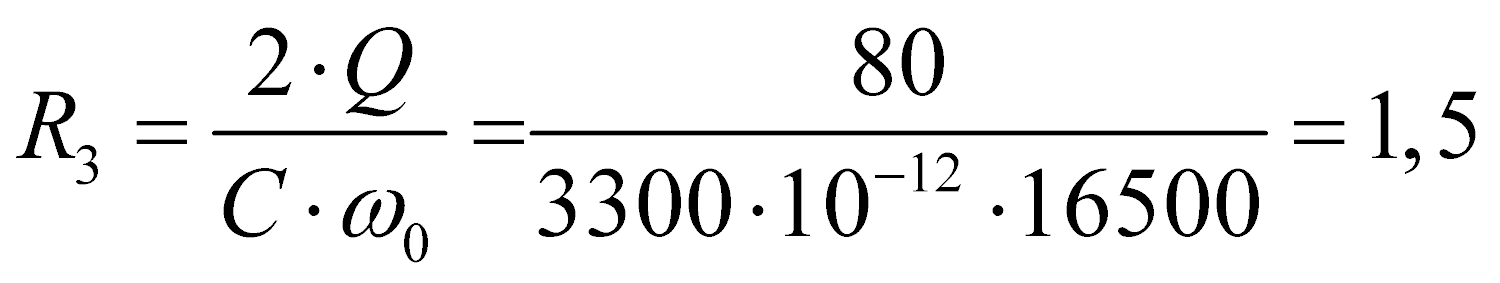 МОм
МОм
Частоту пятого резистивного элемента обычно выбирают случайным образом от одного до нескольких десятков КОм. Выбор пал на 20 кОм., соответственно R5 = 20 кОм.
Для расчета последнего – четвертого резистора требуется для начала выбрать точку смещения, в нашем случае равную E0=2,2 В, тогда:
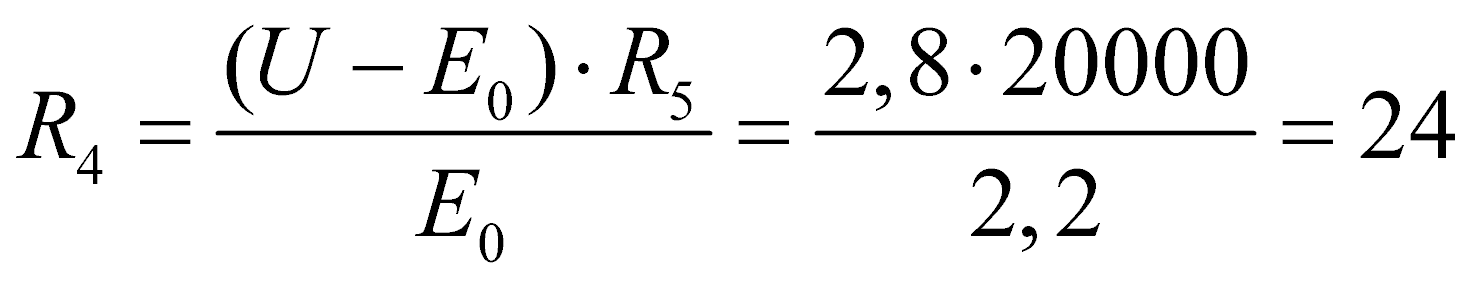 кОм
кОм
Последним этапом расчетов является расчет полосы пропускания
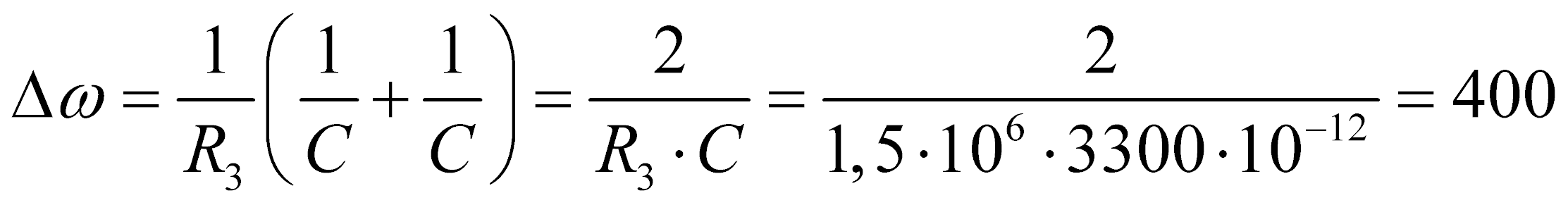 рад/с
рад/с
Переводим полученное значение в Герцы
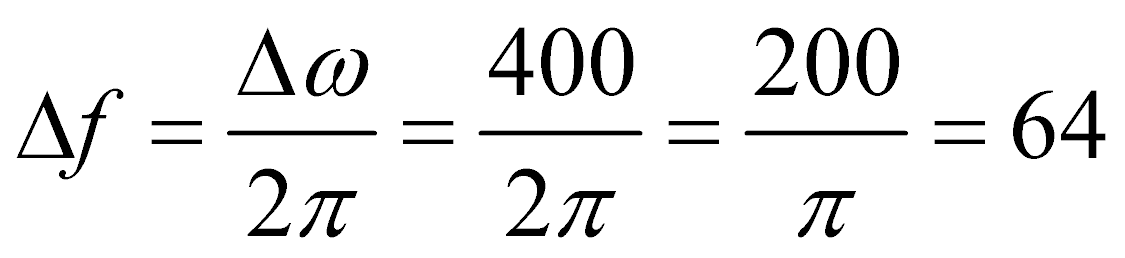 Гц
Гц
На этом расчеты окончены и теперь следует проверить выбранные начальные условия. Для этого подставляем полученные значения в соответствующие формулы
Проверка коэффициента усиления:
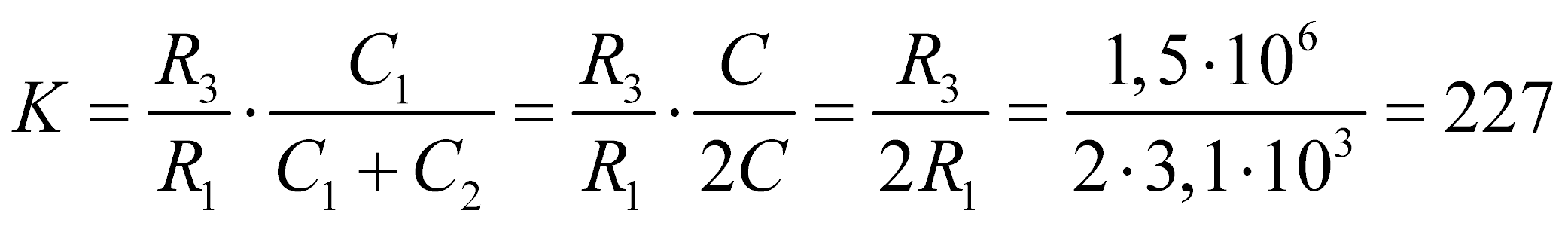 дБ
дБ
Проверка циклической частоты квазирезонанса:
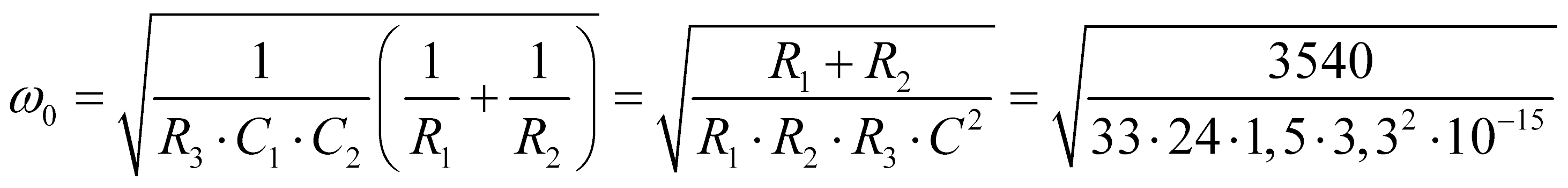 рад/с
рад/с
Проверка частоты квазирезонанса:
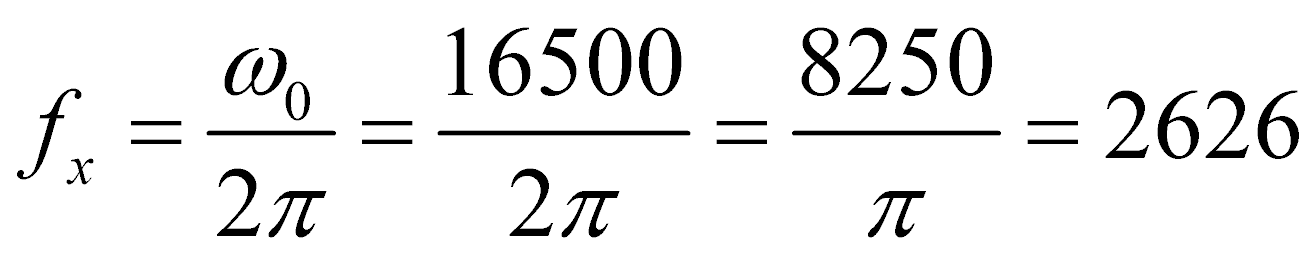 Гц
Гц
Проверка добротности:
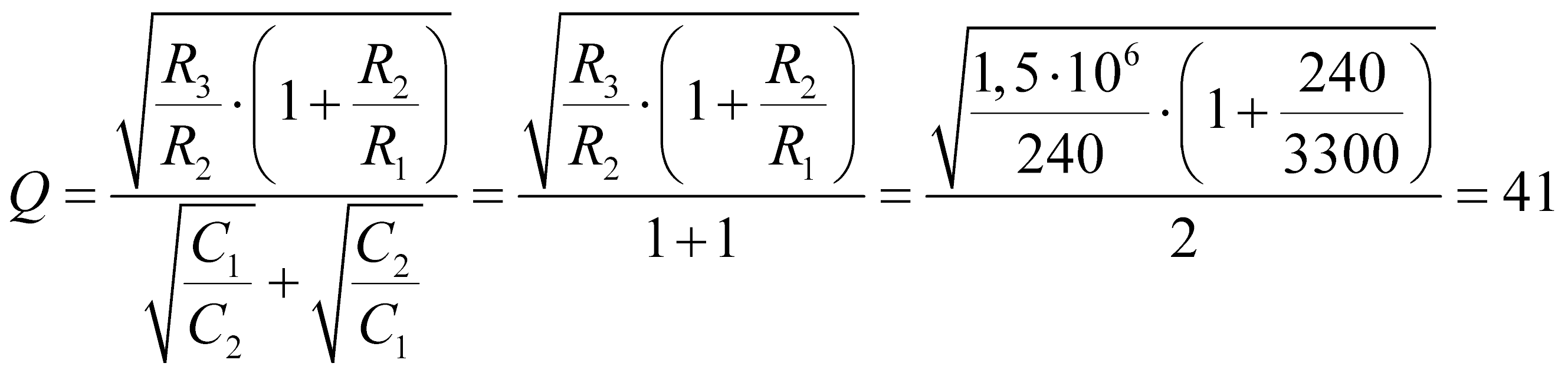
Как видно из всех проверок, погрешность каждого параметра не превышает 3%, что является меньше допустимой погрешности в 5%.
Построим схему этого фильтра (рис. 2) в программной оболочке Micro-Cap 11 и получим АЧХ этого фильтра (рис. 3)
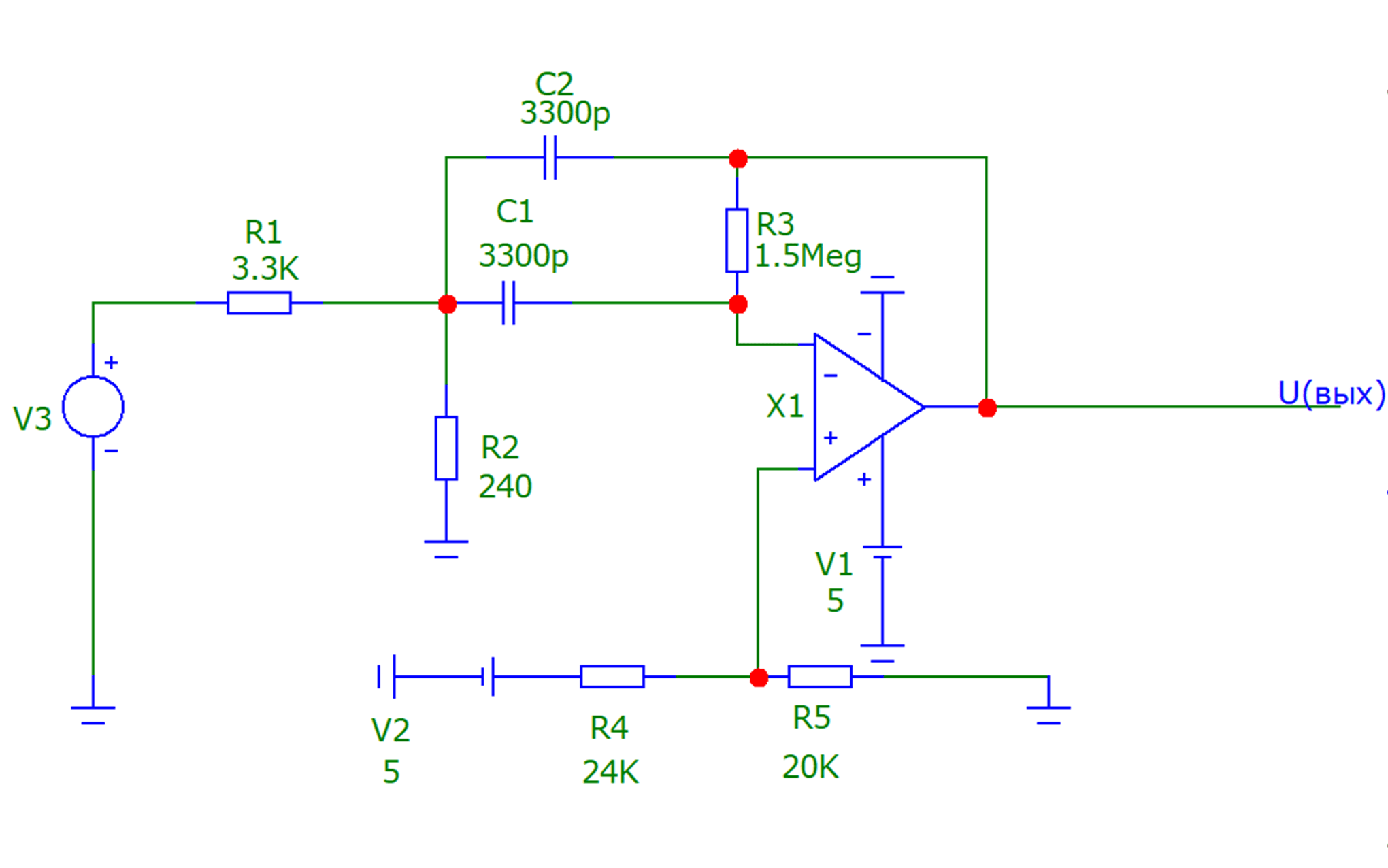
Рис. 2. Схема полосового ARC фильтра в программной оболочке Micro-Cap 11
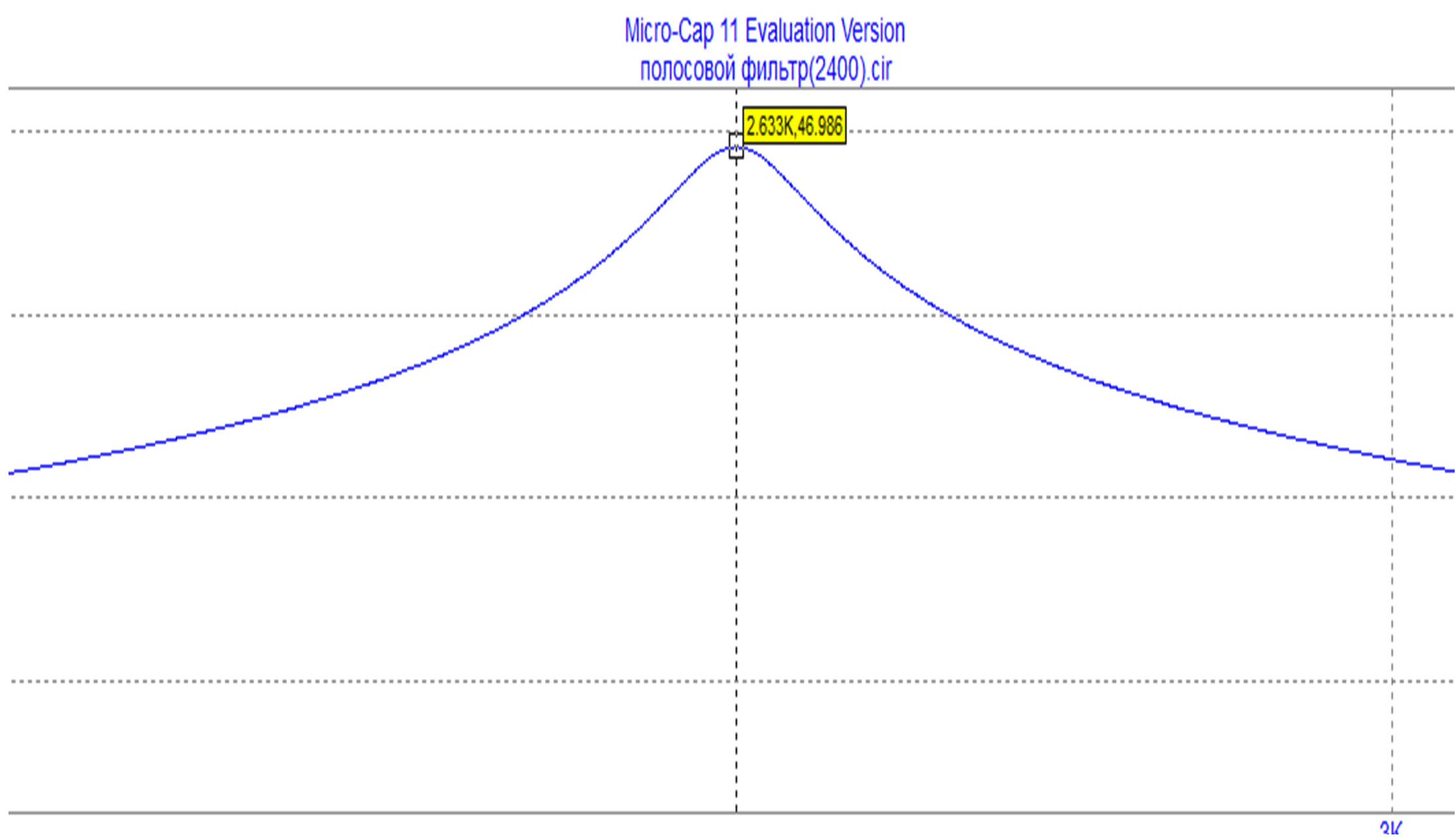
Рис. 3. АЧХ разработанного полосового ARC фильтра
Теперь соберем реальную модель фильтра по рассчитанным выше данным, на базе микроконтроллера Arduino UNO (рис. 4), и также построим его АЧХ в линейном масштабе (рис. 5), для чего напишем программу на языке Python.

Рис. 4. Реальная модель ARC фильтра
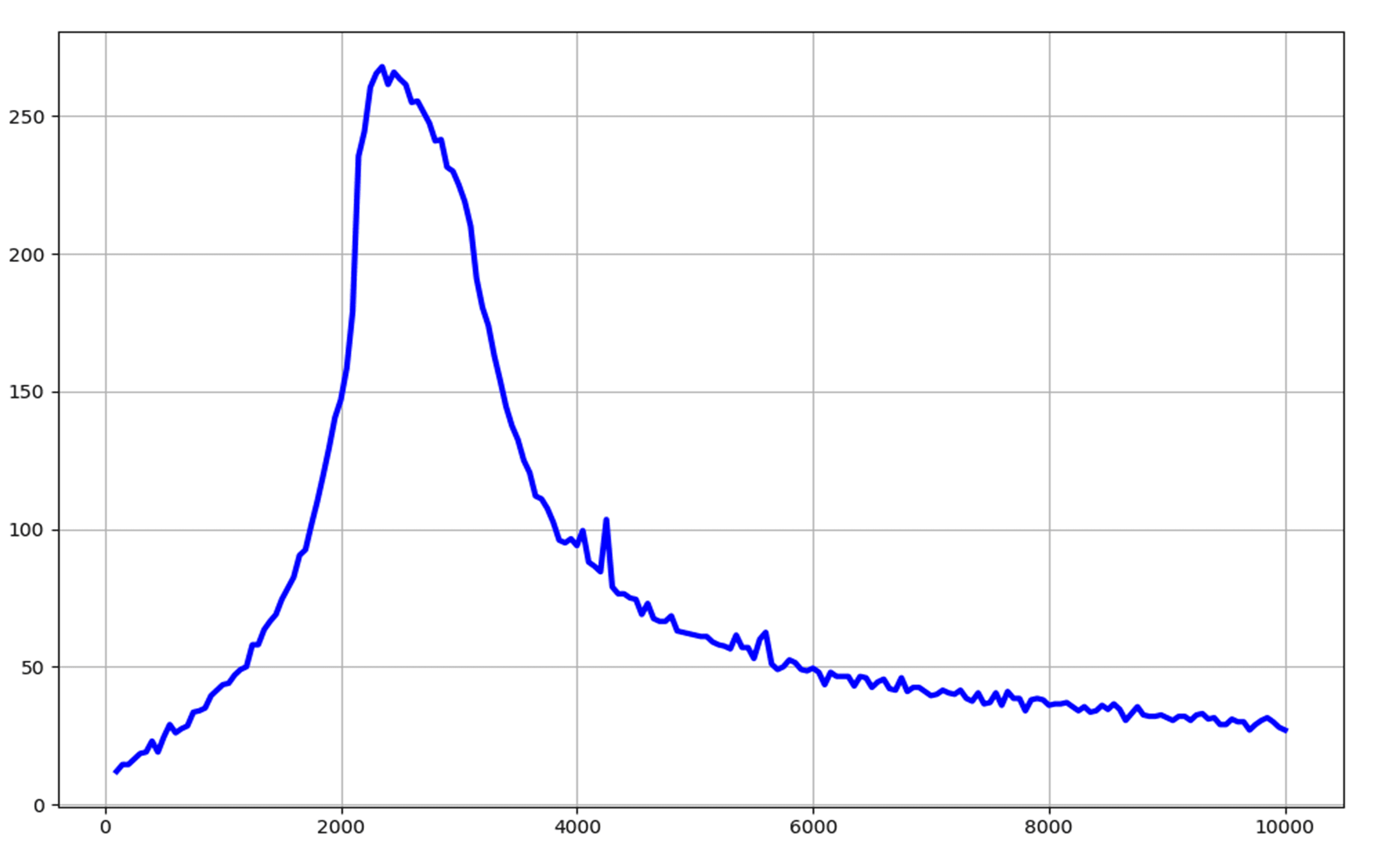
Рис. 5. АЧХ реальной модели ARC фильтра в линейном масштабе
Для сборки фильтра потребовались нижеперечисленные элементы:
- Конденсатор керамический выводной, К10-17Б имп. 3300пФ X7R,10%,0805 (2 шт.)
- Резистор углеродистый CF-25 (С1-4) 0.25 Вт, 240 Ом – 1,5 МОм, 5% (5 шт.)
- Двухканальный операционный усилитель малой мощности LM258N (1 шт.)
- Аккумулятор 5 В (1 шт.)
В заключении стоит выделить ряд выводов:
- В реальном фильтре невозможно добиться параметров как в идеальном, но можно максимально к ним приблизиться
- Реализовать данный активный полосовой фильтр можно на любом типе операционного усилителя, что говорит о простоте и легкости его реализации
- Для измерения выходного сигнала желательно встроить в схему детектор/демодулятор на германиевом транзисторе и RC-цепочке, чтобы замерять не отсчеты высокочастотной синусоиды, а выпрямленный сигнал
- Реальный фильтр неспособен полностью задержать частоты за границами желаемого диапазона частот, в результате имеется область у границ заданного диапазона, где сигнал только частично ослабляется. Эта область называется крутизной спада фильтра, и измеряется в дБ затухания на октаву.

.png&w=640&q=75)