1. Introduction
Due to the increasing progress in the field of hydrogen storage [1, p. 2648-2653] and computational methods, graphene and carbonar structures [2, p. 4955-4962] such as C2B4H6 are suitable alternatives for conventional hydrogen storage systems shortly. In these structures, the DFT density functional theory method is used for modeling, and it is necessary to check its physical equations [3, p. 2032-2037]. In this section, we examine the structures and equations governing the problem. Carbon is one of the amazing elements of nature that has many uses in human life. Chemically, carbon is exactly in the middle of the periodic table, and in terms of electronegativity, it can be considered the middle between metals and non-metals. This atom and some of its relatives have the ability to form four covalent bonds. Another unique property of carbon is that its atoms can be bonded together at arbitrary lengths [4, p. 23723-23730], which is unmatched among other elements. Mixing carbon with metals in a very small amount also shows interesting properties, for example, steel, which is one of the most important engineering alloys, is obtained from the dissolution of about two percent of carbon in iron; Different types of steel can be obtained by changing the percentage of carbon (by only a few hundred percent). A carbon atom has six electrons with an orbital arrangement of 1s2 2s2 2p2, which has four electrons in valence levels [4, p. 23723-23730; 5]. Therefore, a carbon atom has the ability to establish four bonds with other atoms. When the energy difference between the two atomic orbitals is small compared to the bonding energy, as is the case with the 2s and 2p atomic orbitals in carbon, hybrid orbitals form [6, p. 1106-1112], these hybrid orbitals play an important role in the bonding of carbon atoms, and make us achieve different carbon structures. Therefore, a carbon atom has the ability to establish four bonds with other atoms. You can see carbon orbitals in figure 1. When the energy difference between two atomic orbitals is small compared to the bond energy, as is the case with the 2s and 2p atomic orbitals in carbon, hybrid orbitals are formed. These hybrid orbitals play an important role in the bonding of carbon atoms and lead to various carbon structures [7, p. 6177-6185].
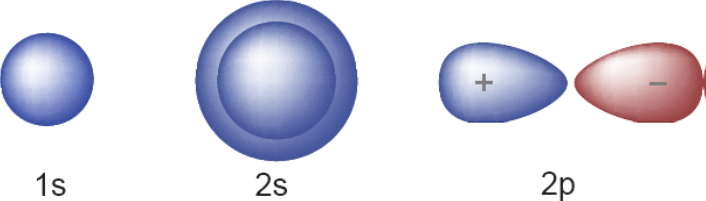
Fig. 1. Carbon atomic orbitals [3, p. 2032-2037]
Graphene is a flat and single-layer material made of carbon atoms. These atoms are connected in a two-dimensional and honeycomb network. Graphene has a thickness of one atom and therefore is known as the thinnest material in the world [8, p. 1741-1752]. Graphene consists of graphite sheets. If we consider graphite as a notebook of parallel sheets, each sheet is called graphene. In a graphene sheet, each carbon atom is covalently bonded to three other carbon atoms. These links are placed in the same plane and the angles between them are equal to 120 degrees. In this case, the carbon atoms are placed in a position that creates a grid of regular hexagons. The carbon-carbon bond length in graphene is about 0.142 nm. Graphene has unique properties that make it a very valuable material [9, p. 337-344]. Graphene is an excellent electrical conductor. Its electrical conductivity is 100 times higher than copper and it is an excellent thermal conductor. Its thermal conductivity is 2000 times higher than that of aluminum. Graphene is one of the hardest materials in the world and its tensile strength is 200 times higher than steel [10, p. 5547-5554]. It is very light and its density is only 2200 kg/m3. Also, graphene has a very high elasticity coefficient. This means it can take a lot of pressure without breaking.
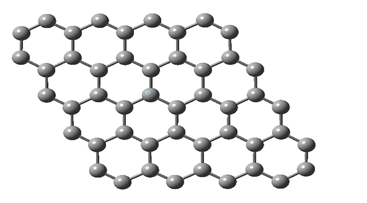
Fig. 2. Graphene hexagonal structure
2. Problem statement and Challenges
The DFT method is a computational method for calculating the structure and properties of materials, which is based on the theory of the density function [8, p. 1741-1752]. This method can be used to calculate hydrogen storage properties in B-doped graphene with hole decorations [11; 12, p. 235-452; 13, p. 11-18; 14, p. 320]. The main challenges of doing this with the DFT method are:
- System size: DFT calculations can be very time-consuming, especially for large systems. In this work, the studied system consists of a graphene sheet with hole atoms. This system is relatively small, but it can still take some time to compute.
- Accuracy of the method: The DFT method is an accurate method for calculating the structure and properties of materials, but it still has some limitations. For example, the DFT method cannot fully account for quantum effects.
- Selection of method parameters: The DFT method has several parameters that must be selected specifically for each system. Choosing inappropriate parameters can lead to inaccurate results.
- In this work, the researchers used the DFT method to calculate the hydrogen storage properties of B-doped graphene with hole decorations. They used a system with hole atoms and used DFT method parameters suitable for graphene and boron. They found that the system can adsorb 6 hydrogen molecules with adsorption energy suitable for recycling under ambient conditions.
Despite the mentioned challenges, the DFT method is a powerful tool for studying hydrogen storage properties in B-doped graphene with hole decorations. This method can be used to predict the properties of this material and guide research in the field of hydrogen storage.
3. Proposed Methodology
Carbon has three hybrid states with symbols sp, sp2, sp3. In the sp state, the 2s orbital is hybridized with one of the 2p orbitals, and in fact, each sp orbital is a linear combination of the two wave functions of the 2s and 2p orbitals [15, p. 41310-41319]:
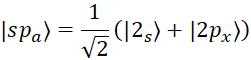 , (1)
, (1)
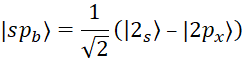 , (2)
, (2)
According to figure 3, for each hybrid, there will be two sp orbital states. In the sp2 state, 2s orbitals are hybridized with two 2p orbitals, and three orbitals are formed according to figure 3 with an angle of 120 degrees. The wave function of this hybrid mode is as follows [15, p. 41310-41319]:
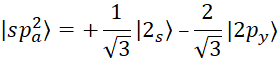 , (3)
, (3)
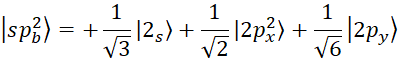 , (4)
, (4)
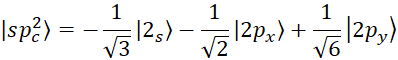 , (5)
, (5)
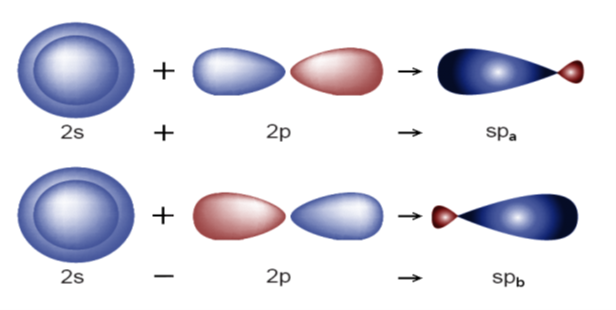
Fig. 3. Sp orbital states
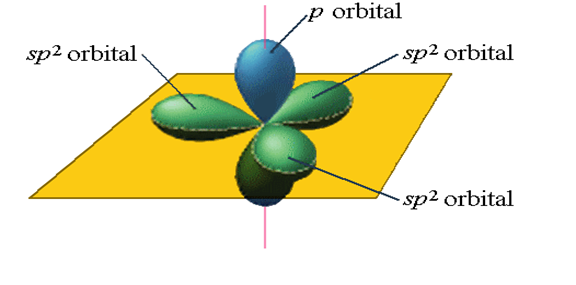
Fig. 4. Sp2 hybrid orbital state
Graphene is a flat and single-layer material made of carbon atoms. These atoms are connected in a two-dimensional and honeycomb network. Graphene has a thickness of one atom and therefore is known as the thinnest material in the world. Graphene consists of graphite sheets. If we consider graphite as a notebook of parallel sheets, each sheet is called graphene. In a graphene sheet, each carbon atom is covalently bonded to three other carbon atoms. These links are placed in the same plane and the angles between them are equal to 120 degrees. In this case, the carbon atoms are placed in a position that creates a grid of regular hexagons. The carbon-carbon bond length in graphene is about 0.142 nm. Graphene has unique properties that make it a very valuable material. Graphene is an excellent electrical conductor. Its electrical conductivity is 100 times higher than copper and it is an excellent thermal conductor. Its thermal conductivity is 2000 times higher than that of aluminum. Graphene is one of the hardest materials in the world and its tensile strength is 200 times higher than steel. It is very light and its density is only 2200 kg/m3. Also, graphene has a very high elasticity coefficient. This means it can take a lot of pressure without breaking.
Graphene is a very promising material that has the potential to change many industries. With the development and commercialization of graphene production technologies, it is expected that this is the material where these atoms are connected in a two-dimensional and honeycomb network, and this is the structure that all graphene materials follow in other dimensions. In fact, graphene is a term that refers to single layers of graphite. If we consider graphite as a book of parallel sheets, each sheet is called graphene. In a graphene sheet, each carbon atom has σ bonds with three other carbon atoms. These three links are placed in one plane and the angles between them are equal to 120 degrees. In this case, the carbon atoms are placed in a position that creates a network of regular hexagons. Of course, this is the most ideal state of a graphene sheet. Also, each carbon atom has a free bond out of the plane. The carbon-carbon bond length in graphene is about 0.142 nm [9, p. 337-344].
Graphene monolayer acts as the underlying structure for carbon nanostructures. When these layers are overlapped, a three-dimensional assembly of graphite is formed, and the interaction between these layers takes place in the form of van der Waals with an approximate distance of 0.335 nm. If a single layer of graphene is wrapped around an axis, a one-dimensional carbon nanotube is formed, and if it is wrapped into a sphere, a zero-dimensional fullerene is formed. Graphene layers with a number of 5 to 10 layers are called thin layer graphene and layers with a number of 20 to 30 layers are called multilayer graphene. Pure monolayer graphene is characterized by quasi-metallic properties [16, p. 114-124]. There are two types of bonds in graphene. One is the σ-type bond that exists between carbon atoms in the graphene plane and is caused by the sp2 hybridization between s, py, and px orbitals and is a covalent bond, so it is very strong and the stability of the graphene structure is also This is the reason. Another bond is the π-type bond, which occurs between orbitals perpendicular to the plane, i.e., pz, and is of van der Waals type.
4. Results and discussions
Using the DFT modeling method, we simulated the structure of graphene and C2B4H6. Now we will examine the results obtained by changing the structure and selected materials. Various phenomena occur in these structures, and it is necessary to investigate their physical processes. In this section, we examine the optical phenomena of the problem.
Two structures of zigzag graphene molecules, one of whose boundary carbon atoms is limited by hydrogen and has an sp2 orbital structure, and the other, in addition to the boundary carbon atoms, other carbon atoms are bonded with hydrogen in the form of chair arms and They are with sp3 orbital structure, in addition, the structure of C2B4H6 and its larger molecules have been investigated with Gossin 09 software by DFT method with B3LYP/6-31G basis. Graphene molecule with zigzag edge arrangement can be investigated by hydrogenating its boundary edges and also its free carbon bonds in the form of two types 1 and 2. Then, the graphene molecule has been simulated in two circular and right-angled arrangements. Both arrangements have zigzag edges. First, the simple graphene molecule without non-carbon bonds and then the hydrogenated graphene molecule, in which the free carbon bond is filled with hydrogen atoms, were designed and calculated using the B3LYP-based DFT method. 3-21G has been structurally calculated and investigated. In the following, the graphene molecule in four structures with different number of carbon and hydrogen atoms, whose zigzag edges are filled with hydrogen, is simulated and calculated based on B3LYP/6-311G by DFT method. has been placed and various quantities have been investigated for all four structures. In the last part, by removing carbon atoms, structures have been obtained which have been simulated by DFT method based on B3LYP/6-31G and compared with structures without defects. The calculations were done at a temperature of 298/150 degrees Kelvin and a pressure of one atmosphere, and the graphs were drawn with Matlab and Gauss Sum software.
4.1 Investigating the properties of zigzag graphene molecular structure
In this section, the graphene molecule with a different number of carbon rings is simulated in different ways with Gossin 09 software by DFT calculation method with B3LYP/6-31G average basis and structurally calculated and investigated. is placed Since we get a more stable material by hydrogenating graphene, and in addition, to improve the efficiency of graphene, its band gap must be modified, hydrogenation is one of the ways to create a band gap in graphene, this section examines the structure of the graphene molecule, which is hydrogenated edge zigzag with sp2 orbital structure and hydrogenated chair zigzag with sp3 orbital structure. Graphene molecules with zigzag edge arrangement can be investigated by hydrogenating their boundary edges and also their free carbon bonds in the form of two types 1 and 2.
Figure 5 shows the 4-ring, 8-ring, and 12-ring structures of the zigzag graphene molecule, whose border carbons are bonded with hydrogen. Dark spheres, atoms of Carbon, and bright spheres are hydrogen atoms and the lines show the bonds between them. In this figure, the orange lines mark the zigzag bond at the edge of the molecule.
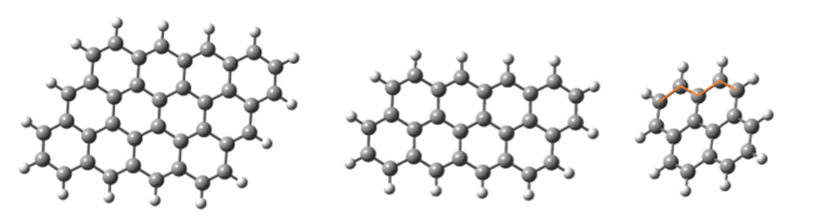
Fig. 5. zigzag graphene structure with the hydrogenated edge (a) 4-ring (b) 8-ring (c) 12-ring
With further calculations in the same way and with the previous basis for 4, 8, and 12 ring structures at 298/150 K, the sum of electron energy and zero-point energy (ground state electron energy at zero K) was checked, which shows the more the hydrogenated edge graphene molecule has a wider structure, due to which it has more electrons, the values obtained for the sum of electron energy and zero-point energy increase. The results are shown in table 1.
Table 1
Modeling calculations of graphene structures
The number of rings | Electron α dipole moment | energy | formation energy | Total electron energy (Hartree per particle) |
4 | 49 | 0 | -515.63 | -755.42 |
8 | 83 | 0.0007 | -1575.26 | -1274.93 |
12 | 116 | 0.0018 | -1275.51 | -1575.10 |
In the continuation of the calculations, the energy level of the highest occupied orbital (HOMO) and the energy level of the lowest occupied orbital (LUMO) were checked for each of the structures with different number of rings, according to the growing trend of the structures, the HOMO energy level descending and the LUMO energy level takes an upward trend. As far as the amount of band gap which is obtained from the difference of HOMO and LUMO energy levels, is reduced by adding benzene rings to the structure. As shown in table 2, the size of the band gap in the 4-ring structure is 0.1420 electron volts, in the 8-ring structure it is 0.0800 electron volts, and in the 12-ring structure, it is 0.0598 electron volts. By reducing this amount, the difference in the size of the band gap between the 4 and 8-ring structure is greater than the similar difference between the 8- and 12-ring structure. Therefore, with the expansion of the structures, the difference in the size of the band gap decreases.
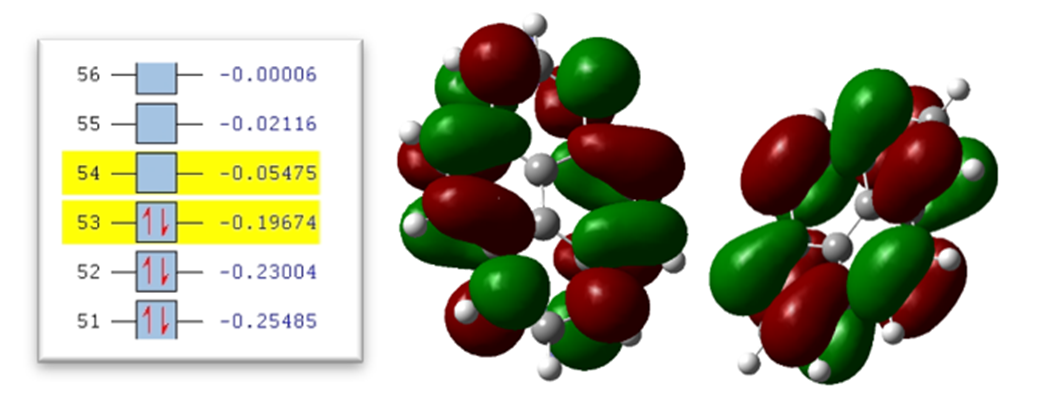
Fig. 6. 4-ring molecule of the first type: (a) HOMO level, (b) LUMO level, and (c) orbital spectrum
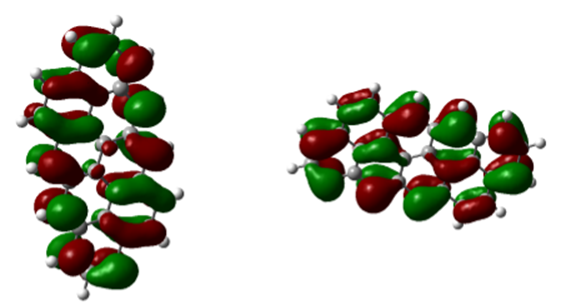
Fig. 7. 8-ring molecule of the first type: (a) HOMO level and (b) LUMO level
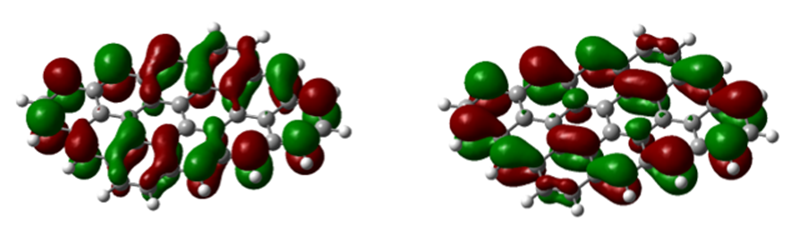
Fig. 8. 12-ring molecule of the first type: (a) HOMO level and (b) LUMO level
In figures 7 to 8, (a) HOMO level and (b) LUMO level are shown with colored shells, which are red, a positive charge density, and shells. The green color shows the negative charge density, which shows the symmetry between the shells in all the images. In figure 7 (c), we see some selections of the spectrum of molecular orbitals, which shows the yellow levels of the LUMO and HOMO levels in terms of electron volts. As indicated, the 53rd orbital shows the HOMO level, which is a filled orbital, and the 54th orbital, which is an empty orbital, shows the LUMO level.
Another issue that was discussed is the calculation of vibrational frequencies according to the intensity of infrared rays (IR). In this study, the first and highest vibration frequencies were considered using the previous method and basis, and the obtained results are listed in table 1. What can be seen in the different structures of this type of graphene molecule, different vibration frequencies were obtained in such a way that as the molecule gets bigger, the first vibration occurs at a lower frequency and the frequency of the highest vibration is increasing. Since we see the first vibration for the 4-ring structure at the frequency of 102.73 cm and for the 12-ring structure at the frequency of 38.60 cm, and with the expansion of the structure, the first vibration occurs at a lower frequency and the difference of this frequency in the structure of 4 and 8 rings is more than the difference of frequency between the structure of 8 and 12 rings. Also, for the 4-ring structure at the frequency of 883.38 cm and the 12-ring structure at the frequency of 3218.33 cm, we see the highest vibration and with the expansion of the structure at a higher frequency, the highest vibration occurs and the difference of this frequency in the 4- and 8-ring structure is more than the frequency difference between the 8- and 12-ring structure. In addition, as the structure of the graphene molecule becomes larger, the frequency interval between the first and the highest vibration becomes larger.
Figure 9 shows the 4-ring and 12-ring structure of the zigzag graphene molecule, where the border carbons and surface carbons are bonded with hydrogen. The dark spheres are atoms. Carbons and bright spheres are hydrogen atoms and the lines show the bonds between them. As shown in the figure, in the chair view, the hydrogen atoms are attached to the carbon atoms halfway from the top and bottom with an almost right angle.
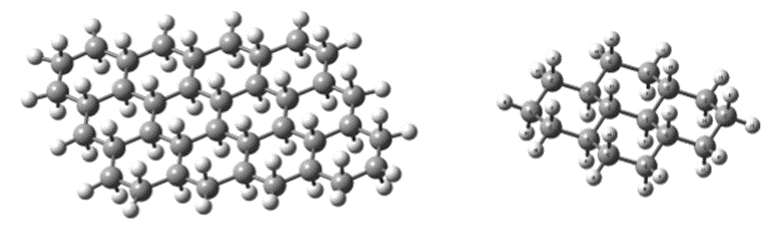
Fig. 9. Structure of hydrogenated zigzag chair graphene molecule (a) 4-ring and (b) 12-ring
Next, the HOMO energy level and LUMO energy level for 4- and 12-ring structures were investigated, and according to the increase in the volume of the structures, both the HOMO and LUMO energy levels decreased. The bandgap size is reduced by adding benzene rings. As shown in the experiment results, the band gap size in the 4-ring structure is 0.3355 electron volts and in the 12-ring structure, it is 0.2939 electron volts. As shown, the size of the band gap in the 4-ring structure of the second-type molecule is greater than the size of the band gap in the similar structure of the first-type molecule, and this is also true for the 12-ring structures. In general, the larger the tape gaff, the more controllable the material is.
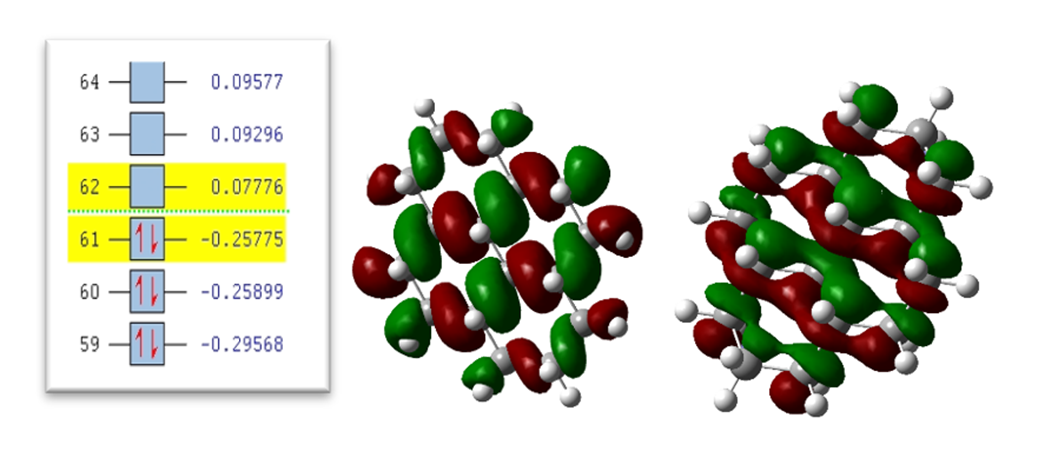
Fig. 10. 4-ring molecule of the second type: (a) HOMO level (b) LUMO level and (c) orbital spectrum
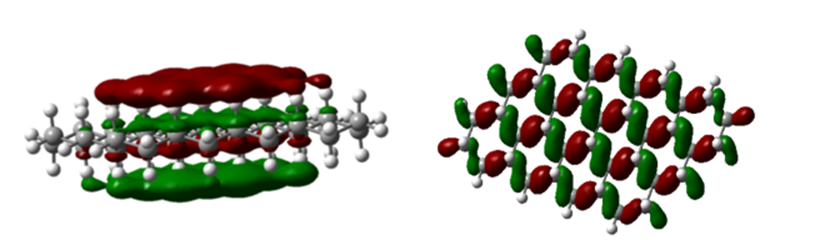
Fig. 11. 12-ring molecule of the second type (a) HOMO level and (b) LUMO level
In figure 11, (a) HOMO level and (b) LUMO level are shown with colored shells, which are red, with positive charge density and shells the green color shows the negative charge density and the symmetry between the shells is visible in each image.
According to the mentioned calculation method and basis, the behavior of vibration frequencies under the intensity of infrared rays was investigated and compared, and for both structures of the second type of molecules, the frequency of their first vibration is close to each other, as well as the frequency of the highest vibration for these two structures, a value with a small difference was obtained. Of course, by comparing the values obtained for the same structures of molecules of the first type and the second type, we find that when the free bonds of the graphene molecule are filled, the first vibration occurs at a higher frequency, and on the other hand, the more free bonds in the If there is a graphene molecule, we see the highest vibration at a higher frequency. As recorded in table 2, the 12-ring structure of the hydrogenated edge graphene molecule will witness its highest vibration at a higher frequency than the rest of the structures mentioned in the table. Because it has more free bonds than other structures. Also, with the size of the structure of the second type graphene molecule, the frequency range between the first and the highest vibration does not differ much.
Table 2
Calculated data of C2B4H6
The number of rings | HOMO (e-volt) | LUMO (e-volt) | The size of tape gaffe (e-volt) | frequency The first vibration (per centimeter) | Frequency Highest vibration |
4 | -0.1996 | -0.0598 | 0.1369 | 69.2 | 34.93 |
8 | -0.1485 | -0.0877 | 0.07 | 25.5 | 79.37 |
12 | -0.1635 | -0.11 | 0.062 | 58.6 | 38.38 |
5. Conclusions and Future Works
We have performed first-principles electronic structure calculations to study the hydrogen storage properties of hole-decorated graphene. A stable and uniform decoration of the single-hole atom on graphene can be obtained by doping B substituents. We find stable geometrical configurations of H2 molecules adsorbed on the hole-decorated graphene sheet. The modified system can adsorb 6H2 molecules with adsorption energy from -0.529 to -0.655 eV/H2, which meets the ideal adsorption energy range for H2 molecules to recycle at near ambient conditions. Electronic structure calculation and analysis show that the hole atom interacts with H2 molecules and graphene through charge transfer. The hole atom becomes a bridge that connects H2 molecules and graphene and improves the adsorption capacity of the graphene sheet for hydrogen storage. Therefore, the modified system shows outstanding potential to become one of the suitable candidate materials for hydrogen storage. As a suggestion, wider graphene structures can be designed and processed with more precise bases. Also, by creating different halides, he achieved more stable and effective structures in different fields of science and technology. In addition, making medicinal compounds from graphene structures has made significant progress in medical physics and reduced the side effects caused by drug consumption. Also, by applying defects to graphene structures and replacing other atoms or molecules, he obtained new compounds and increased the efficiency of graphene structures.

.png&w=640&q=75)