В статье рассмотрим возможности применения среды GeoGebra для решения систем уравнений графическим методом.
Рассмотрим систему: 
Пару чисел 
которая одновременно является решением и первого и второго уравнения системы, называют решением системы уравнений.
Решить систему уравнений – это значит найти все её решения, или установить, что решений нет. Мы рассмотрели графики основных уравнений, перейдем к рассмотрению систем.
Пример 1. Решить систему 
Решение: 
Это линейные уравнения, графиком каждого из них является прямая. График первого уравнения проходит через точки (0; 1) и (-1; 0). График второго уравнения проходит через точки (0; -1) и (-1; 0). Прямые пересекаются в точке (-1; 0), это и есть решение системы уравнений. Для построения графиков функций использовали среду GeoGebra (рис. 1).
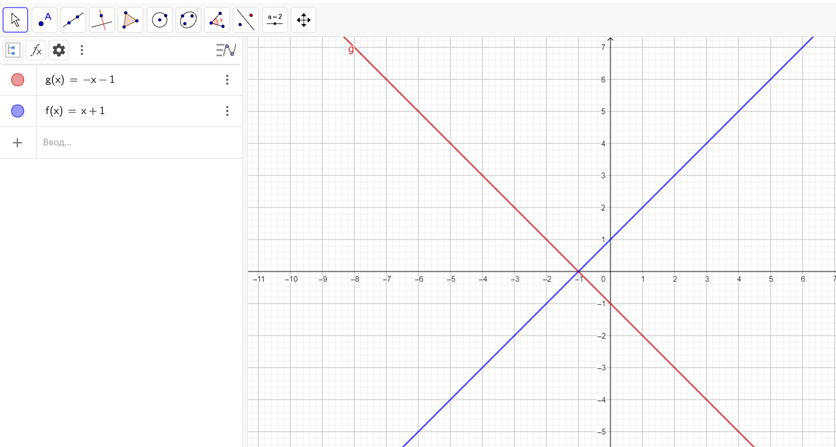
Рис. 1. Пример 1
Решением системы является пара чисел 
Подставив эту пару чисел в каждое уравнение, получим верное равенство.
Мы получили единственное решение системы линейных уравнений.
Ответ: (-1; 0).
Вспомним, что при решении линейной системы возможны следующие случаи:
- система имеет единственное решение – прямые пересекаются,
- система не имеет решений – прямые параллельны,
- система имеет бесчисленное множество решений – прямые совпадают.
Мы рассмотрели частный случай системы, когда p(x; y) и q(x; y) – линейные выражения от x и y.
Пример 2. Решить систему уравнений 
Решение: 
График первого уравнения – прямая, график второго уравнения – окружность. Построим первый график по точкам (рис. 2).
| x | 0 | -1 |
| y | 1 | 0 |
Центр окружности в точке О(0; 0), радиус равен 1.
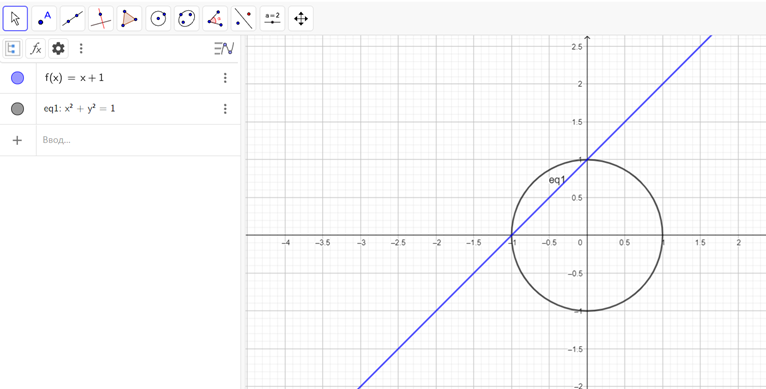
Рис. 2. Пример 2
Графики пересекаются в точках А(0; 1) и В(-1; 0).
Ответ: (-1; 0); (0; 1).
Пример 3. Решить систему графически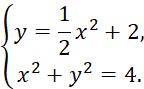 
Решение: графиком первого уравнения является парабола. Она сдвинута относительно начала координат на 2 вверх, т. е. ее вершина – точка (0; 2) (рис. 3). Графиком второго уравнения является окружность с центром в точке О(0; 0) и радиусом 2.
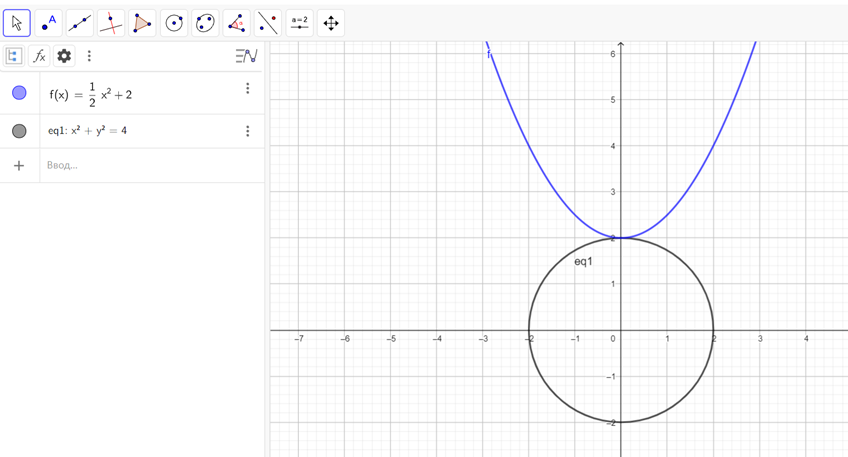
Рис. 3. Пример 3
Графики имеют одну общую точку – т. А(0; 2). Она и является решением системы. Подставим пару чисел в уравнение, чтобы проверить правильность.
Ответ: (0; 2).
Пример 4. Решить систему 
Решение: Построим график второго уравнения – это окружность с центром в точке О(0; 0) и радиусом 1.
Построим график функции 
Это ломаная. Теперь сдвинем ее на 1 вниз по оси oy. Это и будет график функции 
.
Поместим оба графика в одну систему координат (рис. 4).
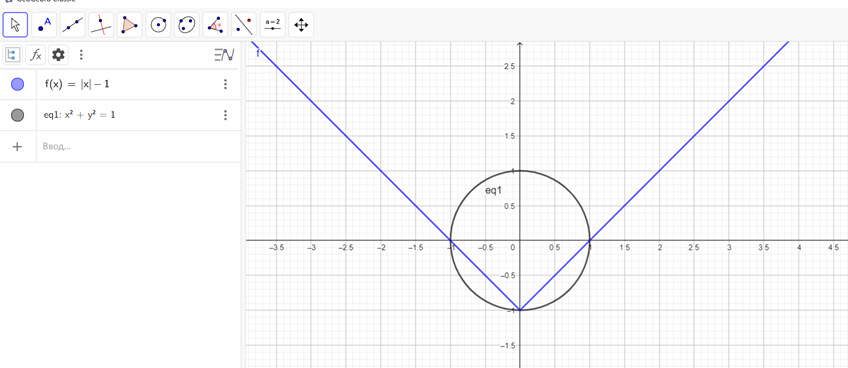
Рис. 4. 15
Получаем три точки пересечения – А(1; 0), В(-1; 0) и С(0; -1).
Ответ: (-1; 0); (0; -1); (1;0).
Среда GeoGebra позволила продемонстрировать возможности построения графиков функций. Данный материал можно применять на уроках алгебры 7–9 классов. Динамическую среду GeoGebra рекомендуем также принять на уроках геометрии для построения геометрических фигур на плоскости и в пространстве [1, с. 152-154].
Применяя информационные технологии в обучении математики ребята выступают в роли исследователей, которые вооружены простыми средствами, позволяющими им провести анализ, наблюдение, эксперимент и зафиксировать показания изучаемого объекта и процесса исследования [2, с. 88-91].
Учебно-методический комплекс Мордковича А. Г. рассматривает возможности систематического внедрения в курс алгебры 7–9 классов задач с параметрами [3].
Демонстрация различных графиков функций (прямая, парабола, гипербола и окружность) в среде GeoGebra позволяет обучающимся не только стоить, а проводить исследования по выявлению частных случаев расположения графиков функций.
