Метод диагностики деструкции полимерной оболочки кабелей

Введение

Нарушение изоляции силовых кабелей, с последующим самовозгоранием и разрушением изоляции приводят к значительным убыткам и катастрофам. В настоящее время требуется разработка профилактических испытаний изоляции силовых кабелей неразрушающими методами, что позволяет оценивать остаточный ресурс и прогнозировать вероятность потери работоспособности кабеля в процессе его эксплуатации [1, c. 690]. Следует отметить, что широко применяемый контроль сопротивления изоляции не в полной мере дают информацию об остаточном ресурсе кабеля. Измерения абсорбционных характеристик, динамических вольтамперных характеристик, реверсивных и термостимулированных токов являются технически сложно реализуемыми методами. Предложенная методика контроля свойств кабелей с резиновой изоляцией на основе анализа температурной зависимости электропроводности [2, с. 536] также трудно реализуема при промышленной эксплуатации кабеля и его закреплении в пучке трассы.

Актуальной является разработка ускоренного метода определения технического состояния кабельной изоляции, выбор диагностических параметров, которые, изменяясь со временем по мере старения изоляции, непосредственно связаны с процессом изменения свойств изоляции.

Подобным диагностическим параметром является твердость материала изоляции, величина, существенно изменяемая в процессе старения изоляции [2, с. 536].

Материалы и методы контроля

1. Особенности кабелей с резиновой изоляцией

Отличительной особенностью кабелей является наличие шланговой изоляции типа РШН; изоляция жилы выполняется из резин типа РТИ. Известно, что для подобных материалов доминирующим механизмом старения резины является протекание реакций окислительного дегидрохлорирования полихлоропрена, сопровождающихся изменением структуры пространственной сетки:

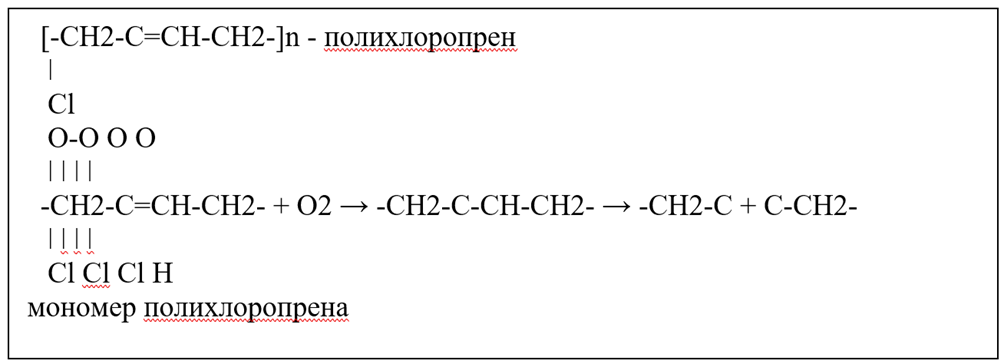
Рис. 1

Наличие в молекуле атома хлора реакционная способность соседней с ним двойной связи понижается. Поэтому энергия активации первичного акта присоединения кислорода для полихлоропрена выше, чем для неполярных каучуков, и окисление полихлоропрена при невысоких температурах протекает медленно. Однако образование двух полярных групп в одном участке цепи (атом хлора, кислородная группа) и появление, в связи с этим возможности отщепления хлористого водорода создают условия для ускорения процесса окисления, особенно при повышении температуры. Таким образом, при повышенных температурах полихлоропрен не обладает высокой стойкостью к старению.

Фактический срок службы кабелей не ограничивается тем, что указан в технических условиях, а определяется состоянием кабелей к концу срока их службы. В процессе эксплуатации за счет десорбции наполнителей (рис. 2), протекающих химических реакций кабель теряет массу, изменяется эластичность, гибкость, становится жестким. На его оболочке и изоляции жилы возникает сетка мелких трещинок, а затем – трещины, открывающие доступ влажному воздуху, загрязнениям вплоть до металлической жилы. При этом в отсутствие загрязнений в сухом воздухе электрическое сопротивление кабеля с трещинами в объеме изоляции может оставаться относительно высоким, но оно резко падает во влажной или агрессивной среде [3].

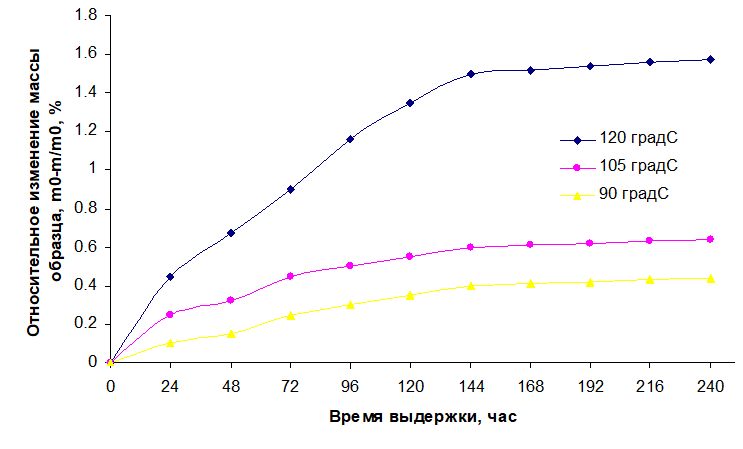
Рис. 2. Потери массы образцов кабеля КГ в процессе старения при различных температурах

Анализ и опыт эксплуатации кабелей с резиновой изоляцией показывает, что срок службы кабелей фактически ограничивается временем до момента появления трещин на поверхности шланговой изоляции кабеля [4, c. 46].

2. Объекты испытаний и методика обработки результатов

Оценкой качества изоляции до появления трещин может выступать диагностический параметр – твердость материала, предельное значение которого достигается в течение срока службы.

Оценка степени старения материала кабелей реализуется путем измерения твердости Н_i (HSA) материала изоляции по методу Шора. Твердость измеряется цифровым переносным измерителем твердости типа ТПЩ-ПАЦ, с диапазоном измерения твердости от 0 до 100 HSA. Преимущество данного метода является возможность определения твердости изоляции кабелей непосредственно в процессе эксплуатации, в том числе под напряжением без демонтажа трассы.

Проводили измерение твердости шланговой изоляции на основе анализа данных выборки из n = 10 изменений. В ходе статистической обработки полученных данных рассчитывали: среднее значение Н, абсолютная погрешность ∆Н с учетом коэффициента t_n Стьюдента (доверительная вероятность P = 0,95). В предположении, что экспериментальные данные описываются нормальным законом распределения, производили расчет функции распределения F(x) и плотности распределения f(x) стандартными методами [2, c. 693].

Исходная изоляция кабелей характеризуется эластичными свойствами, и величина твердости шланговой изоляции для кабеля КГ составляет H_из.ш = (81,3 ± 2,9) HSA.

Ускоренные испытания по старению кабельной изоляции (КГ), проводимые при температурах 105°С и 120°С (рис. 3), показали, что при средних значениях твердости в диапазоне H_из.ш = (96,1 ± 0,5) HSA на поверхности шланговой изоляции появляются сквозные трещины.

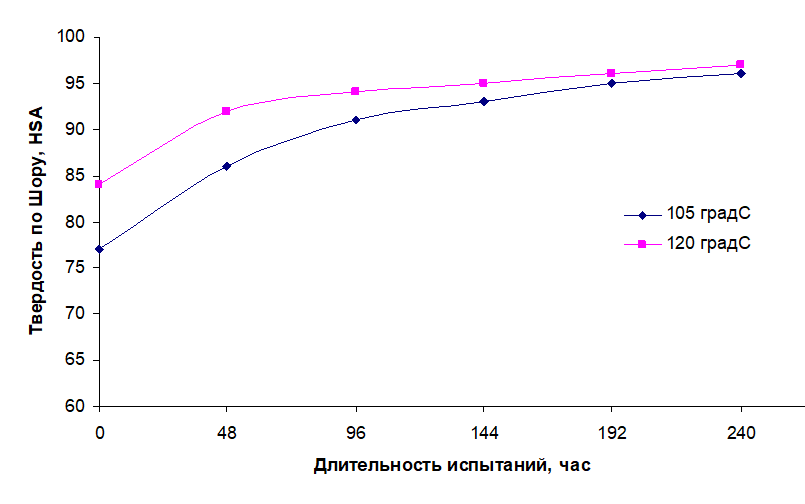
Рис. 3. Ускоренные испытания образцов кабеля КГ с измерением величины твердости при температурах 105°С и 120°С

3. Анализ вероятностных функций

Анализ качества деструктирующей изоляции с учетом оценки средних значений твердости Н (изоляции жилы или шланга) показывает, что данный диагностический параметр не является достаточно информативным, поскольку параметры твердости Н_i изоляции элементов выборки изменяются в широких пределах.

Более достоверным является анализ вероятностных функций характеристик изоляции кабеля. В процессе измерений значения H_i твердости анализируемой выборки, каждое значение твердости H_i – случайная величина, принимающая одно из возможных значений твердости в пределах определенного промежутка от Н_min до Н_мах в процессе измерений. Совокупность значений выборки как значений случайной величины образуют статистический ряд. Для анализа такого ряда применяют разнообразные числовые характеристики статистики: среднее значение Н (математическое ожидание), стандартное отклонение σ и т. д. Характеристикой случайной величины твердости Н является закон распределения, имеющий две формы представления: функция распределения F(H), определяющая вероятность появления случайной величины, принимает значения от 0 до 1 (интегральная функция); плотность распределения – f(H) = dF(H)/dH (изменяется в пределах от 0 до 1), показывающая вероятность попадания случайной величины в заданный интервал и ее наиболее вероятные значения.

Для описания твердости резиновой изоляции применяли нормальный закон распределения. Использовали следующий алгоритм определения функции и плотности распределения [2, c. 693]:

• проведение испытания параметров твердости и определение выборки H_i;
• расчет среднего значения Н и стандартное отклонение σ;
• определение пределов изменения случайной величины с учетом закона трех сигм (генеральная совокупность): Н_min = Н – 3σ; Н_мах = Н + 3σ, округляются полученные значения;
• вычисление шага δH изменения случайной величины для определения интервала изменения генеральной совокупности: δH= (Н_мах – Н_min)/n, где n – количество значений в возможном интервале, задаваемом при испытании;
• определение массива вероятных значений изменения величины H_i через шаг δH от Н_min до Н_мах;
• вычисление значения функции распределения F(H) и плотности распределения f(H) с помощью функции нормального распределения;
• построение графиков функции F(H) и плотности распределения f(H).

Данный алгоритм реализуется с полученным массивом величины твердости с помощью программы Excel или другими аналогичными программами с помощью статистических функций.

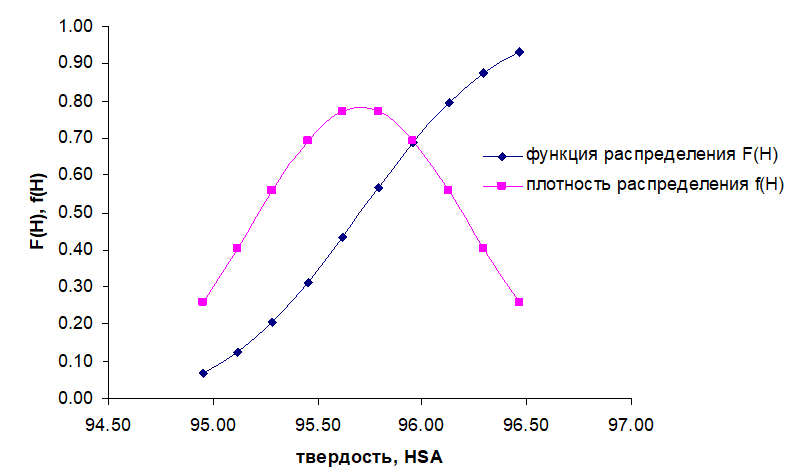
Рис. 4. График функции F(H) и плотности распределения f(H) при температуре 105°С

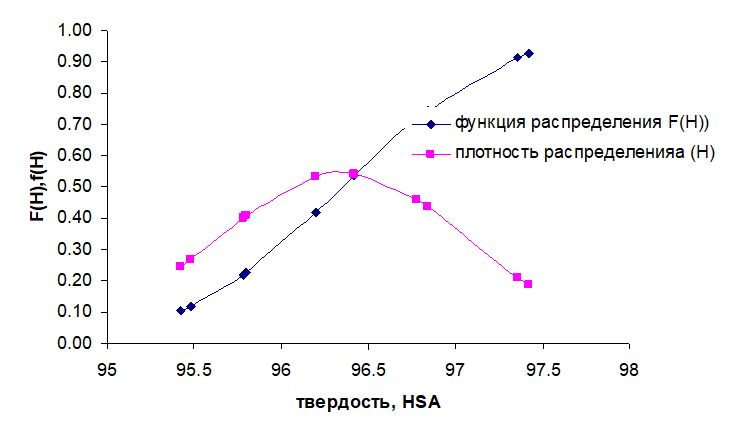
Рис. 5. График функции F(H) и плотности распределения f(H) при температуре 120°С 

Удовлетворительное совпадение расчетных и экспериментальных данных на графиках функции распределения и плотности распределения (рис. 4 и рис. 5) подтверждает выдвинутое предположение о нормальном законе распределения.

Рассматривают следующие варианты оценки:

• Определение вероятности случайной величины твердости Н при условии «не менее» заданного значения функции распределения F(Н). Пример: (рис. 4) вероятность того, что значение Н будет не менее 95,8 HSA равна F = 0,6;
• Определение величины Н по заданной величине функции распределения F(Н). Пример (рис. 5), вероятность F = 0,5 справедлива для значений Н ≤ 96,5 HSA.
• Определение по плотности распределения f(H) вероятность появления каждого значения случайной величины. Пример: (рис. 4), наиболее вероятно появление значения твердости изоляции, равного 95,7 HSA, так как наиболее вероятным значением случайной величины является ее математическое ожидание.

Выводы

Представленные результаты исследований твердости шланговой изоляции и изоляции жилы показывают, что предлагаемая методика позволяет выявить объективные статистические параметры твердости материала и производить диагностику качества изоляции в процессе эксплуатации без демонтажа кабельных трасс.

Превышение твердости материала изоляции жилы и шланговой изоляции выше определенных пределов является характеристикой аномального технического состояния кабельных трасс, предвестником процесса интенсивного трещинообразования и, как следствие, нарушения электроизоляционных свойств изделия.

Наиболее эффективным является проведение одновременных испытаний по анализу твердости изоляции и тепловизионной диагностики кабельных трасс, в ходе которой определяется карта теплового поля объекта и локализация участков с повышенной температурой [4, с. 45-47].

Изменение качества изоляции кабелей переносным измерителем твердости актуально при оценке реального технического состояния судовых сетей и выбраковке состаренных участков кабельной трассы.