Сравнительный анализ методов кластеризации социальных графов на данных социальной сети «ВКонтакте» по мере сходства двух разбиений и модулярности

Введение: социальные сети представляют собой графы, которые могут быть ориентированными – с направленными связями, или взвешенными, где каждой связи присвоено определённое значение. Это открывает возможность использования методов кластеризации, опирающихся на графовую теорию.

Упрощая граф, устраняется направленность и добавляется вес к существующим связям, преобразуя его в матрицу, что позволяет получить данные, эквивалентные набору характеристик несвязанных объектов. В таком контексте связь между вершинами становится дополнительной характеристикой, что позволяет применять стандартизированные методы кластеризации, не прибегая к графовым теориям.

Выбор алгоритма кластеризации зависит от характеристик и типа данных, которые используются при построении графа. Применяя различные алгоритмы, можно выявлять кластеры и ключевые узлы, что способствует лучшему пониманию динамики социальных связей. Важно учитывать, что структура сетей играет решающую роль: кластеры с высокой связностью могут оказывать более сильное влияние на участников, чем разрозненные группы [1].

В этом контексте особое внимание уделяется алгоритмам, которые используют доступные данные о пользователях, позволяя преобразовывать информацию в количественные показатели для определения степени близости между узлами. На основе данных из социальной сети можно вычислять веса рёбер графа, выявляя более значимые связи между пользователями.

При построении графа необходимо учитывать как множества(узлы), так и ребра (бинарные отношения) между ними. Особенно важным является параметр веса, который отражает характер взаимодействия пользователей. Работа с API «ВКонтакте» позволяет получать необходимые данные для расчёта близости построенных отношений [2]. А в качестве весомых признаков использовать совместные показатели пользователей.

При этом важно продолжать совершенствовать информативность социального графа: эксперименты по выбору параметров и анализ их влияния на вес рёбер открывают интересные возможности для исследования и экспериментов.

Сбор и обработка данных

В данной работе учтены дружеские связи второго уровня (друзья друзей) «обезличенного» пользователя социальной сети «Вконтакте». Для этого было использовано API данной сети. Был прописан модуль на языке Python для получения данных пользователей, учитывались возможные ошибки со стороны API, ограничение на число запросов кратным 5000, а также для увеличения скорости обработки методы отрабатывались «батч» запросами. В модуле учитывалось получение количественных, качественных данных и текстовых описаний групп и постов пользователей. Полученные данные записывались в разных форматах pkl, gml, json. В дальнейшем полученные характеристики пользователя будут использованы для модификации текущего кластерного анализа.

В частности, использовались следующие методы VK_API:

• get – метод для получения списка друзей.
• getMutual – метод для поиска общих друзей (создания рёбер в графе).
• get – метод для получения групп друзей.

На основании собранных данных формируется взвешенный неориентированный граф, в котором каждая вершина соответствует пользователю социальной сети. Для каждого узла извлекается список сообществ (групп), в которых состоит пользователь, с помощью функции get_user_groups, а также вычисляется количество общих друзей с другими пользователями через метод get_mutual_friends.

Для определения весов рёбер было принято решение использовать метрику Jaccard-сходства, так как она позволяет количественно оценить степень перекрытия между множествами – в данном случае, между списками групп и друзьями. Итоговый вес каждого ребра рассчитывается как сумма Jaccard-сходств по двум аспектам: группам и друзьям. Это позволяет учесть как тематическую близость пользователей (через интересы), так и их структурную связанность (через общих друзей), делая граф более информативным для последующего анализа и кластеризации. Итоговая формула для расчёта веса ребер графа для каждой пары узлов:

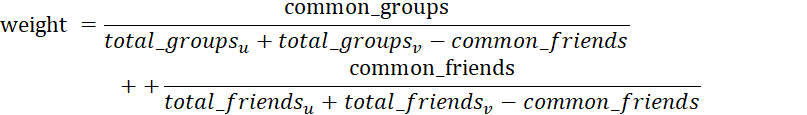, (1)

Где:

weight – весовая категория атрибута;

common_groups – количество общих групп пары узлов;

common_friends – количество общих друзей пары узлов;

– объединение групп;

– объединение друзей.

Этот подход позволяет учитывать как общие интересы (группы), так и социальную близость (общие друзья), что делает граф более информативным для анализа социальных отношений.

Чтобы улучшить качество дальнейшего анализа, стоит также обработать полученные данные. Для этого удаляем изолированные узлы. Это позволит сосредоточиться на наиболее значимых связях.          В результате был получен граф с 1549 узлами, 1628 связями и общим количеством уникальных групп 79011. Визуализация одной из окрестностей графа с помеченными на удаление узлами на рисунке.

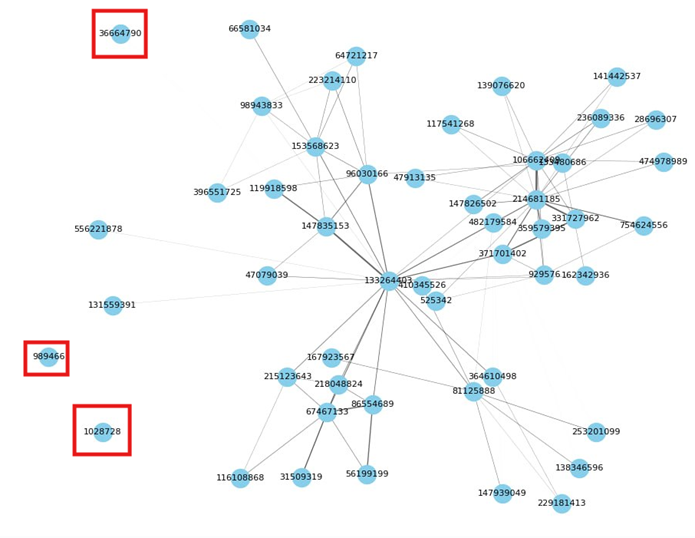
Рис. Визуализация выборки из графа

Методы кластеризации

Для кластеризации полученного графа были использованы следующие алгоритмы: Edge Betweenness (Метод Гирвана-Ньюмана) [3, с. 7821-7826], Label Propagation (Распространение меток) [4], Fastgreedy (Жадная оптимизация модульности) [5] и Louvain (Оптимизация модульности) [6]. В дальнейшем за n будем обозначать количество вершин в графе, а за m – количество ребер.

Метод Fastgreedy (Greedy Modularity Optimization) представляет собой иерархический агломеративный алгоритм, ориентированный на максимизацию модульности – функции, оценивающей качество разбиения графа на сообщества. Алгоритм начинается с того, что каждая вершина рассматривается как отдельное сообщество. На каждом шаге он жадно объединяет такие пары сообществ, слияние которых приводит к наибольшему приросту модульности. Этот процесс повторяется до тех пор, пока модульность перестаёт возрастать или все вершины не объединены в одно сообщество.

Основным преимуществом Fastgreedy является прямолинейность и высокая интерпретируемость, поскольку на каждом шаге можно отслеживать, какие объединения происходят и почему. Однако он может «застревать» в локальном максимуме, не находя глобально оптимального разбиения. В отличие от Louvain, Fastgreedy не использует фазу агрегации и работает исключительно по стратегии последовательного слияния.

Алгоритм эффективно работает с взвешенными графами, учитывая силу связей между узлами. Тем не менее он плохо масштабируется на очень большие графы, поскольку требует повторного пересчёта модульности на каждом шаге.

В типичном случае временная сложность Fastgreedy составляет O(n log² n) для разреженных графов, однако в общем случае она может достигать O(n² log n), что делает его пригодным в первую очередь для небольших и средних сетей.

Label Propagation. Алгоритм функционирует на основе эвристического правила, согласно которому вершина присоединяется к тому сообществу, которое преобладает среди её соседей. В начальной стадии каждая вершина рассматривается как отдельная группа. Далее, в ходе итераций, их порядок изменяется случайным образом, и каждое обновление происходит на основании присвоенных меток соседних вершин. Этот процесс продолжается до момента, пока структура кластеров не стабилизируется. Из-за случайной природы метода несколько его запусков могут приводить к разным результатам, что делает его неустойчивым. Алгоритм характеризуется интуитивной логикой, простотой реализации и высокой вычислительной скоростью, так как его сложность приближается к O(m).

Edge Betweenness. Разработанный Гирваном и Ньюманом метод базируется на вычислении центральности рёбер. В самом начале определяется через какие связи проходит наибольшее количество кратчайших путей между различными вершинами. Далее рёбра с наиболее высокими показателями центральности удаляются, а оставшиеся после этого компоненты рассматриваются как отдельные кластеры. Этот процесс продолжается до достижения максимального значения модулярности. Метод имеет несколько модификаций, основанных на изменении используемых метрик или применении альтернативных функций разбиения. Основным его недостатком является высокая вычислительная сложность, поскольку оценка центральности связей требует значительных ресурсов. Алгоритм работает за O(m²n).

Louvain. Метод основан на жадном поиске локального оптимума модулярности и использует технику локального перемещения вершин (LMH). Алгоритм последовательно перемещает вершины между сообществами таким образом, чтобы каждое действие увеличивало показатель модулярности. Обход вершин осуществляется в произвольном порядке и завершается, когда дальнейшие перемещения перестают приводить к улучшению структуры кластеров. В первой фазе алгоритм анализирует соседние вершины, поочередно изменяя их принадлежность к группам, если это способствует увеличению модулярности. Вторая фаза выполняет агрегацию: вершины одного сообщества сливаются в единый узел, а рёбра между ними преобразуются в новые связи. Этот процесс повторяется, пока итоговая структура графа остаётся неизменной, а модулярность не достигает локального максимума. Несмотря на то, что порядок обхода вершин может повлиять на производительность, он не оказывает значительного влияния на финальный результат. В среднем метод работает за O (n log n).

Практическая часть

Результаты работы алгоритмов оценивались двумя метриками, модулярностью и NMI (мера сходств двух разбиений).

Модулярность (modularity) – это числовая метрика, которая измеряет, насколько хорошо граф разбит на сообщества. Она сравнивает долю рёбер внутри сообществ с ожидаемой долей таких рёбер в случайном графе той же степени связности. Значение модулярности Q лежит в диапазоне от -1 до 1 и интерпретируется следующим образом:

• Q → 1 – отличное разбиение: большинство рёбер находится внутри сообществ, а не между ними. Это говорит о чётко выраженной кластерной структуре.
• Q ≈ 0 – нейтральное (почти случайное) разбиение: рёбра расположены примерно так же, как в случайном графе, и сообществ как таковых не выделяется.
• Q < 0 – плохое разбиение: больше рёбер между сообществами, чем внутри них. Это означает, что текущая кластеризация хуже, чем случайное разбиение. Математически модулярность графа определяется как:

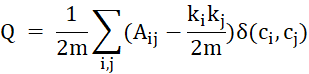, (2)

Где:

m – общее количество рёбер в графе;

A_ij – элемент матрицы смежности (1,если есть ребро между i и j, иначе 0);

k_i, k_j – степени вершин i, j;

– ожидаемое число рёбер между i и j в случайном графе;

δ(c_i, c_j) – индикатор: 1,если i и j в одном кластере, иначе 0.

Так как в исходных данных отсутствовала истинная разметка (ground truth), отражающая принадлежность пользователей к конкретным сообществам, было принято решение создать её вручную. Для этого использовалась эвристическая стратегия, основанная на предположении, что пользователи с большим количеством общих друзей и групп, скорее всего, принадлежат к одному сообществу. Если у пользователя не было выраженной связи с другими (например, слишком мало общих групп и друзей), ему присваивалась метка ближайшего соседа – то есть того пользователя, с которым у него наибольший вес связи в графе. Чтобы оценить, насколько хорошо алгоритмы кластеризации находят сообщества, согласующиеся с этой гипотезой, использовалась метрика нормализованной взаимной информации (NMI). Она позволяет сравнивать результат кластеризации с эталонной (эвристической) разметкой. Чем выше значение NMI, тем сильнее совпадение между тем, что "нашёл" алгоритм, и тем, что мы задали вручную.

NMI (Нормализованная взаимная информация) – это способ сравнить два разбиения множества, основанный на взаимной информации (например, предсказанные кластеры и вручную размеченные группы «ground truth»).В основе NMI лежит взаимная информация (MI) – она измеряет, насколько знание одного разбиения уменьшает неопределённость (энтропию) другого. NMI нормализует это значение, чтобы результат всегда находился в диапазоне от 0 до 1:

• 0 означает полное несоответствие между кластерами;
• 1 означает полное совпадение (разбиения идентичны).

Это делает NMI удобной для оценки качества кластеризации, особенно когда классы и кластеры не совпадают по числу или размеру, но могут всё равно хорошо соответствовать друг другу по составу.

Формула NMI метрики:

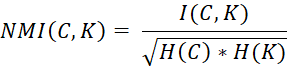, (3)

Где: C – предсказанные кластеры;

K – ground truth метки (истинные сообщества);

I(C, K) – взаимная информация между C и K;

H(C) и H(K) – энтропии каждого разбиения.

Поскольку некоторые алгоритмы кластеризации обладают стохастической природой и могут выдавать различные результаты при повторных запусках (например, из-за случайного порядка обновления узлов или инициализации меток), для повышения достоверности оценки каждый метод был выполнен трижды. Далее для анализа рассматривались наилучшие значения метрик по результатам этих запусков. Итоговые значения модулярности и нормализованной взаимной информации (NMI), демонстрирующие наилучшее качество кластеризации для каждого метода, представлены в таблице.

Таблица

Полученные оценки методов

Данные таблицы позволяют сделать вывод, что с учетом особенностей нашего социального графа и проставленной нами разметке Louvain демонстрирует наибольшие показатели как по модулярности, так и по NMI. Fastgreedy также показывает хорошие результаты, но уступает Louvain. Label Propagation и Edge Betweenness менее эффективны, особенно по критерию модулярности, что может быть связано с их спецификой работы на графовых социальных сетях.

Заключение

В рамках данной работы был реализован программный модуль, предназначенный для сбора пользовательских данных из социальной сети «ВКонтакте». На основе собранных данных был сформирован взвешенный неориентированный граф, в котором вершины соответствуют пользователям, а рёбра отражают степень социальной близости, рассчитываемую на основе количества общих друзей и пересечения интересов (групп). Вес рёбер формировался как сумма Jaccard-сходств по этим двум аспектам, что позволило учесть как структурные, так и семантические характеристики пользовательских связей.

Для анализа полученного графа был проведён сравнительный эксперимент с применением наиболее известных алгоритмов детекции сообществ: Louvain, Fastgreedy, Label Propagation и Edge Betweenness. Рассмотрены теоретические и вычислительные особенности указанных методов, проанализирована устойчивость разбиений и их интерпретируемость. Каждый алгоритм оценивался с использованием таких метрик, как модулярность (modularity) и нормализованная взаимная информация (NMI), отражающая соответствие разбиения заданным меткам.

По результатам экспериментов, наилучшие показатели продемонстрировали алгоритмы Louvain и Fastgreedy, причём первый показал более стабильную и интерпретируемую структуру сообществ. Несмотря на высокую модульность, метод Fastgreedy оказался менее эффективным в обнаружении «естественных» кластеров. Алгоритмы без учёта весов (например, Label Propagation) показали меньшую точность и высокую вариативность результатов между запусками.

Таким образом, было продемонстрировано, что качественный выбор алгоритма детекции сообществ, адаптированного под особенности конкретного графа и весовой модели, является критически важным для получения содержательной структуры кластеров и извлечения значимой информации из социальной сети.