Кривые Безье в видеоиграх

Введение

Кривая Безье – это математически описанная кривая, которая определяется несколькими контрольными точками. Кривые Безье являются фундаментальным математическим инструментом, который широко применяют в компьютерной графике, анимации, в видеоиграх и во многих других областях. Основное преимущество данных кривых заключается в их простоте и гибкости: они позволяют точно задавать сложные криволинейные траектории с помощью набора контрольных точек, влияющих на форму кривой в соответствии с полиномиальными функциями Бернштейна. Это делает их особенно удобными для задач моделирования, где требуется плавное изменение геометрии. В видеоиграх наиболее распространены кривые Безье второй и третьей степеней (квадратичные и кубические) для анимации и создания эффектов. Эти кривые позволяют плавно изменять параметры (например, позицию, вращение) объектов, создавая визуальные эффекты и плавные движения. Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже.

Виды кривых Безье и их практическое применение

1. Линейные кривые

Линейные кривые Безье – это простейший вид кривых Безье, состоящий всего из двух опорных точек: начальной (P₀) и конечной (P₁), при n = 1 (рис. 1).

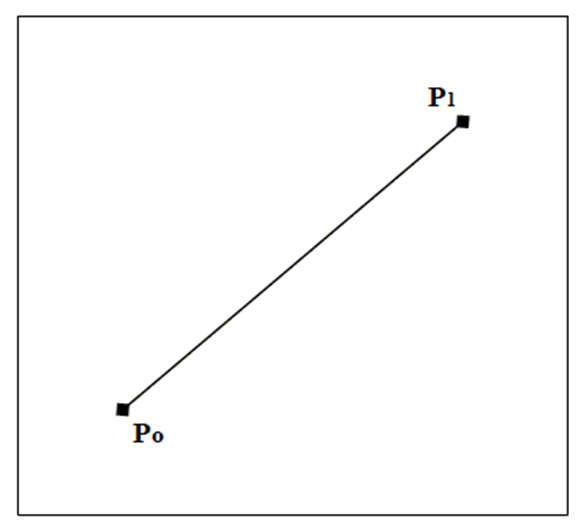
Рис. 1. Линейная кривая Безье

Уравнение линейной кривой Безье задаётся интерполяцией между P₀ и P₁ (рис. 2):

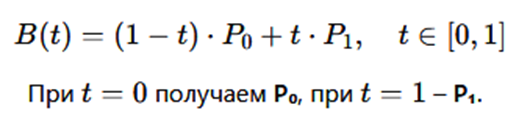
Рис. 2. Уравнение линейной кривой Безье

Практическое применение:

• Основной строительный блок для более сложных кривых Безье (квадратических, кубических и т. д.).
• Анимация и интерполяция – плавное перемещение объекта из точки P₀ в P₁ с линейной скоростью.
• Векторная графика – задание прямых сегментов в контурах фигур (например, в SVG).

Следовательно, линейные кривые Безье являются фундаментом для более сложных кривых, а также удобным способом работы с прямыми линиями в параметрическом виде.

2. Квадратичные кривые

Квадратичная кривая Безье (n = 2) (рис. 3) задаётся тремя опорными точками:

• P₀ – начальная точка,
• P₁ – контрольная точка (определяет «натяжение» кривой),
• P₂ – конечная точка.

Она позволяет строить параболические дуги и используется там, где нужны плавные, но не слишком сложные изгибы.

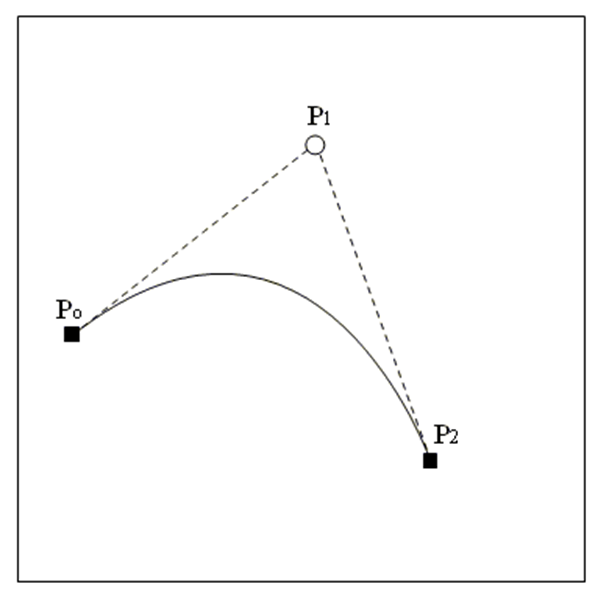
Рис. 3. Квадратичная кривая Безье

Кривая задается следующим параметрическим уравнением (рис. 4):

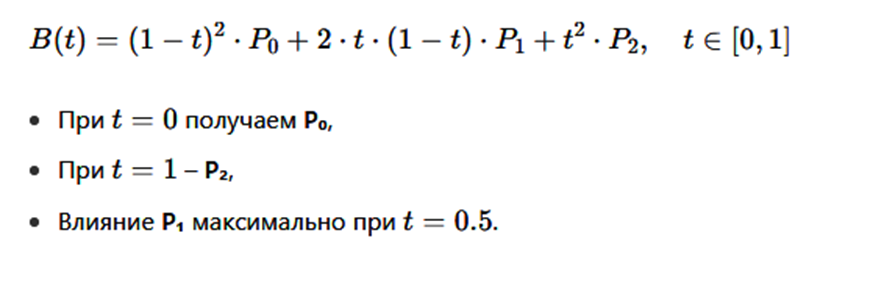
Рис. 4. Параметрическое уравнение квадратичной кривой Безье

Практическое применение:

• Простая векторная графика (SVG, шрифты, логотипы).
• Сглаживание углов (например, скруглённые кнопки в UI).
• Движение по параболе (анимация прыжков, траектории в 2D-играх).
• Построение более сложных кривых (кубические Безье часто разбивают на квадратичные для упрощения расчетов).

3. Кубические кривые

Кубическая кривая Безье – это гладкая параметрическая кривая, определяемая четырьмя точками (рис. 5):

• P₀ – начальная точка,
• P₁ и P₂ – две контрольные точки (управляют формой кривой),
• P₃ – конечная точка.

Она позволяет создавать S-образные изгибы, петли и сложные гладкие формы, что делает её одной из самых популярных кривых в компьютерной графике.

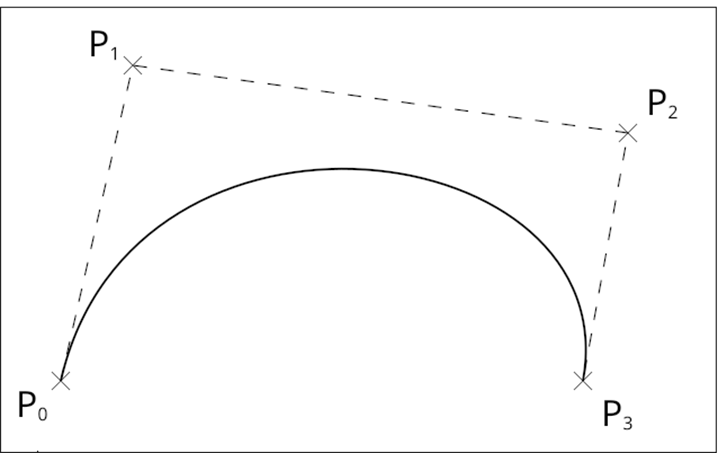
Рис. 5. Кубическая кривая Безье

Кубическая кривая задается следующим параметрическим уравнением (рис. 6):

Рис. 6. Параметрическое уравнение кубической кривой Безье

Практическое применение:

• Векторная графика (SVG, Adobe Illustrator, CorelDRAW, Figma).
• Анимация и easing-функции.
• Построение 3D-поверхностей. В программах типа Blender или AutoCAD кубические Безье используются для создания плавных полигональных mesh-объектов.

Кубические кривые Безье – это достаточно мощный инструмент для создания гладких, сложных форм в графике, анимации и 3D-моделировании. Они менее производительны, чем квадратичные, но гораздо гибче.

Использование кривых Безье в видеоиграх

Кривые Безье – один из ключевых инструментов в разработке видеоигр, обеспечивающий плавность, управляемость и реалистичность движения. Ниже будут рассмотрены примеры использования в разных аспектах игрового процесса:

1. Движение персонажей и объектов

Кривые Безье широко используются в играх и анимации для задания плавных, управляемых траекторий движения персонажей, камер, снарядов и других объектов. Они позволяют:

• Создавать сложные пути (петли, S-образные движения, спирали).
• Контролировать скорость и плавность (через параметризацию).
• Динамически изменять маршрут (например, для ИИ противников).

Патрулирование NPC:

• Враги или союзники перемещаются по заданным маршрутам (например, караульные в стелс-играх). Пример: В Metal Gear Solid кривые Безье задают пути патрулей.
• Траектории снарядов - гранаты, магические атаки или пули с эффектом кривизны (как в Worms).
• Платформеры и паркур. Автоматическое сглаживание прыжков по сложным траекториям (Super Mario Odyssey).

2. Анимация камеры:

• Кинематографические кат-сцены. Камера плавно перемещается между точками, сохраняя драматичность (The Last of Us). Инструменты: Unity – Cinemachine Spline, Unreal – Cine Camera Actor.
• Динамическое слежение. Камера следует за игроком, избегая препятствий (Racing games).

3. Физика и столкновения:

• Коллайдеры сложной формы. Аппроксимация кривыми для точного определения столкновений (2D-платформеры).
• Верёвки и тросы. Динамическая симуляция на основе сплайнов (Uncharted 4).

4. Генерация миров и уровней:

• Процедурные дороги и рельсы. В симуляторах (Cities: Skylines) или гоночных играх (Forza Horizon) кривые Безье помогают создавать извилистые пути.
• Реки, мосты, декор. Природные объекты сглаживаются для реалистичности (Red Dead Redemption 2).

5. Визуальные эффекты (VFX):

• Траектории частиц. Дым, огонь или магические следы движутся по кривым (Hogwarts Legacy). Инструменты: Unity – Particle System, Unreal – Niagara.
• UI-анимации. Плавные переходы меню, прогресс-бары (Cyberpunk 2077).

6. ИИ и навигация:

• Кривые Безье идеально подходят для создания плавных и естественных маршрутов движения NPC, мобов или юнитов, особенно когда стандартные алгоритмы поиска пути (A*, NavMesh) дают угловатые или «роботизированные» траектории.

7. Будущее кривых Безье:

• Более сложные кривые (например, рациональные Безье – NURBS).
• Рендеринг без тесселяции – в реальном времени (например, в ray tracing).
• Нейросетевые аппроксимации – автоматическая оптимизация форм.

Как кривые Безье работают в игровых движках

1. Аппроксимация и тесселяция

Кривые Безье редко рендерятся напрямую – обычно они разбиваются на:

• Линейные сегменты (в растеризаторах).
• Треугольники (в 3D-графике, например, при рендеринге NURBS).

2. Оптимизации:

• Рекурсивное разбиение (de Casteljau algorithm) – для динамического LOD (Level of Detail).
• Аппаратное ускорение – в современных GPU (например, в DirectX 12 Mesh Shaders).
• Кэширование – предрасчёт кривых для анимаций.
• Использование сплайновых инструментов – в Unity (Cinemachine), Unreal (Spline Mesh).

3. Интеграция с физикой:

• Коллайдеры сложной формы – аппроксимация кривыми.
• Траектории в симуляциях – например, движение воды или верёвок.

4. Готовые решения в популярных движках

Unity:

• Cinemachine – для кинематографичных путей камеры.
• LeanTween – анимация по кривым.
• Bezier Path Creator (ассет из Asset Store).

Unreal Engine:

• Spline Component – готовая система для движения объектов.
• Niagara – траектории частиц на основе Безье.

На рисунке 7 представлена таблица с примерами использования кривых Безье в конкретных движках/технологиях:

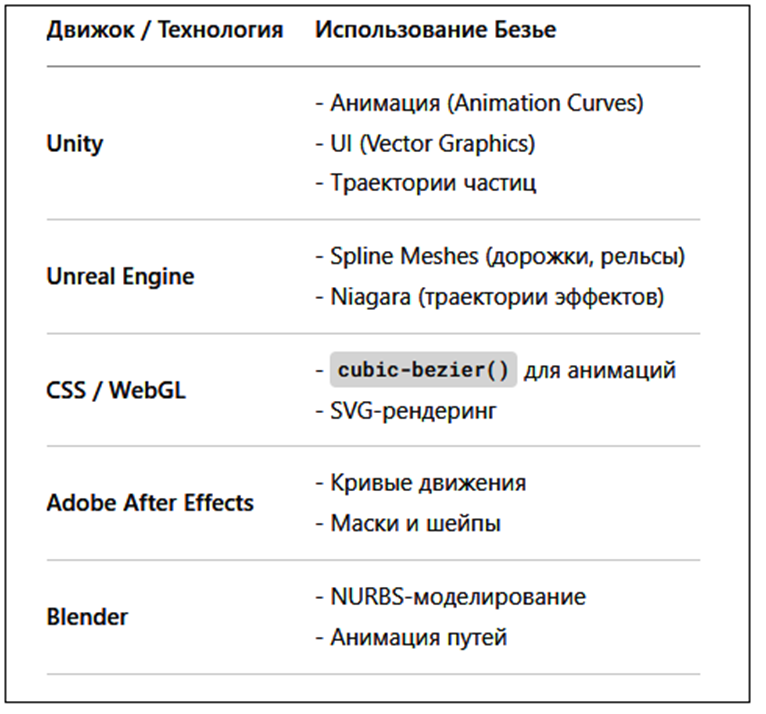
Рис. 7. Таблица применения кривых Безье в конкретных движках

Заключение

Кривые Безье – это одна из ключевых технологий в компьютерной графике, который применяют везде: от рендеринга до анимации и физики. Современные движки оптимизируют их разными способами, но суть остаётся той же: гладкие, параметрически управляемые кривые, которые позволяют создавать сложные формы с минимальными вычислительными затратами.

Они являются стандартом для решения многих игровых задач и поддерживаются во всех игровых движках (Unity, Unreal, Godot). Их интеграция с современными алгоритмами может привести к созданию еще более реалистичных и интерактивных виртуальных миров.

Таким образом, кривые Безье остаются фундаментальным инструментом в арсенале геймдизайнеров и программистов, а их изучение и оптимизация продолжают оставаться актуальными направлениями исследований в области компьютерной графики и игровых технологий.