Введение. В работе рассматривается конструкция обратной связи для задачи оптимального конфликтного управления конкретным динамическим объектом – материальной точкой на горизонтальной плоскости [4]. Критерий качествапроцесса управления – расстояние от точки на плоскости в конечный момент времени до заданного центра (начала координат). Так как для конфликтно-управляемой динамической системы не выполняется так называемое условие седловой точки для маленькой игры [9] эффективное решение задачи установлено в классе смешанных стратегий в классе смешанных стратегий [2, 4, 12], т.е. используется некоторый вероятностный механизм формирования управления. Задача на минимакс выбранного критерия качества решается в рамках концепции, разрабатываемой в уральской школе по оптимальному управлению и дифференциальным играм Н.Н. Красовского [7, 8, 12] и решается методом экстремального сдвига на сопутствующие точки, предложенным автором [3, 5]. Основную роль в рассматриваемой конструкции играет некоторая модель-поводырь. Работа продолжает исследования автора по решению задач оптимального управления по принципу обратной связи [2, 4, 12].
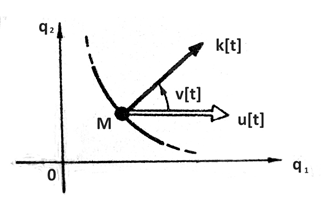
Рис. 1. Движение объекта
Движение объекта. Рассмотрим объект (материальная точка М), двигающийся в горизонтальной плоскости в декартовой системе координат {q1, q2} под действием силы k[t] из работы [4] (рис. 1), описываемый векторным нелинейным дифференциальным уравнение в форме второго закона Ньютона [10]
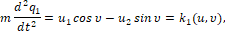
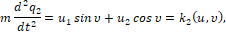
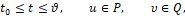(1)
где u1, u2 – суть проекции вектора силы управления u на оси q1, q2 (рис. 1), υ – помеха – угол люфта управляющей силы, t – время, начальный и конечный моменты времени t0 и ϑ зафиксированы, P и Q – соответственно множества векторов u и углов υ, определяющие ресурсы органа управления U и органа V, вырабатывающего помехи (рис.2).В данном конкретном примере [4] множества P и Q определены следующим образом
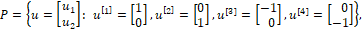
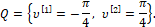(2)
Приведем систему (1) к нормальной форме [7]. Введем фазовый вектор
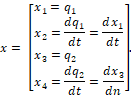(3)
Тогда система (1) в нормальной форме принимает вид
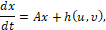
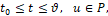
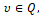(4)
где
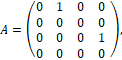
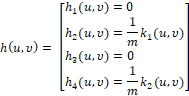(5)
Показатель качества. Как и в работе [4], цель управления – минимизировать расстояние от точки М в конечный момент времени t=ϑ от некоторого центра О (рис. 1). Тогда показатель (критерий) качества процесса управления задаётся в виде функционалаγ от движения
q[t0[⋅]ϑ] = {q[t], t0≤t≤ϑ} объекта (1-5)
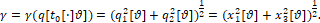(6)
Модель-поводырь. Будем рассматривать задачу [1-9, 11, 12] о выборе управленийu помех υ, соответственно минимиизирующих и максимизирующих критерий качества γ (6). В рассматриваемом случае для объекта (4, 5) не выполняется условие седловой точки для маленькой игры [9], т.е. – равенство
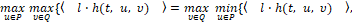
для любого вектора l ∈ R4. Известно, что в этом случае задача эффективно решается в классе, так называемых, смешанных стратегий [2, 10]. При этом используется некоторый вероятностный механизм для конструирования управлений
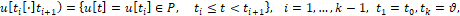
где P – набор из четырёх единичных, взаимно перпендикулярных векторов (2) и
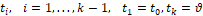(7)
моменты выбранного разбиения отрезка времени управления. В рассматриваемом случае роль такого поводыря для движения реального объекта играет некоторая виртуальная у-модель, включаемая в следующую схему управления по принципу обратной связи (рис. 2).
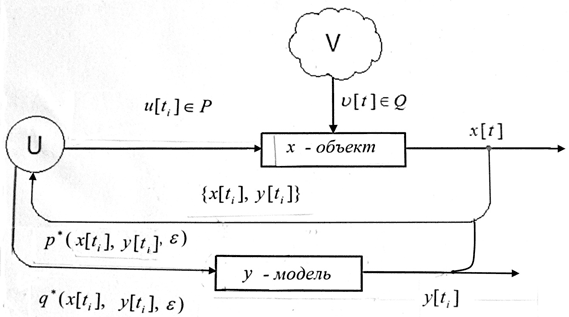
Рис. 2. Схема управления по принципу обратной связи в классе смешанных стратегий
Состояние такой компьютерной модели в текущий момент времени t определяется ее фазовым вектором y[t], размерность которого совпадает с размерностью фазового вектора x (3). Дифференциальное уравнение у-модели строится следующим образом. Каждой четверке аргументов t, x, y, ε, где ε>0 – некоторый малый параметр, выбираемый нами самими и влияющий на точность решения задачи, поставим в соответствие наборы чисел
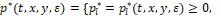
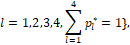
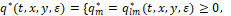
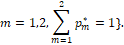(8)
Движение у-модели-поводыря определяется как решение пошагового дифференциального уравнения
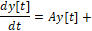
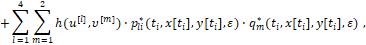
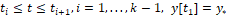(9)
при выбранных разбиении (7) и условиях (2), (5), (8).
Смешанная стратегия. Ключевым моментом рассматриваемой задачи является построение оптимальнойсмешанной стратегии управления, формирующей движение х-объекта (4), (5) по шагам выбранного разбиения (7). А именно, назовём смешанной стратегией в процессе управления с у-моделью-поводыремсовокупность S трёх функций
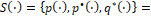
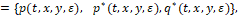(10)
где функция
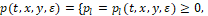
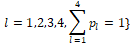(11)
участвует в построении движенияx-объекта (4), (5) следующим образом. Движение объекта есть решение пошагового дифференциального уравнения
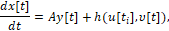
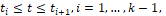
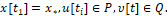(12)
Здесь
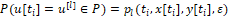(13)
Символ P(B) обозначает вероятность события В, P– множество (2). В (12) помеха – есть реализация помехи
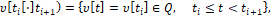
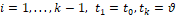– кусочно-измеримая по времени t функция – воздействие, формируемое либо внешней средой, либо предполагаемым противником в органе V (рис. 2).
Оптимальная смешанная стратегия
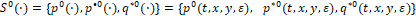
существует [2, 12]. При этом для её построения используются два метода – метод экстремального сдвига на сопутствующие точки, предложенный автором [3, 5, 12] и метод взаимного устойчивого отслеживания движении реального объекта (4) и его виртуальной модели-поводыря (9) [6, 12]. Реализация траектории движения объекта (1), порожденного оптимальной смешанной стратегией при конкретных исходных данных приведена в работе [4].
