Метод экстремального сдвига для оптимального управления в позиционной дифференциальной игре

Введение.

Рассматриваются в игровой постановке задача оптимального управления по принципу обратной связи динамической системой, которые описывается нелинейными дифференциальными уравнениями. Особенность рассматриваемых задач – в неполноте информации о помехах, действующих на управляемый объект. Критерии качества процесса управления задаются в виде функционалов от движения объекта. Такие задачи занимают достаточно большое место среди задач управления в технике, экономике и т.д. Приводятся методы построения оптимальных алгоритмов. Рассматриваемая задача продолжает исследования авторов [2, 3] по определению оптимальных алгоритмов управления в рамках концепции Екатеринбургской школы по управлению и дифференциальным играм Н.Н. Красовского [4-6].

Объект управления. Рассматривается конфликтно-управляемый объект, движение которого описывается нелинейным векторным дифференциальным уравнением

 x=f(t, x, u, υ), t₀≤t≤ϑ, u∈P, υ∈Q,   (1)

  |f(t, x, u, υ)| ≤ χ⋅(1+|x|), χ=const

где x – n-мерный вектор, t – время, начальный и конечный моменты времени t₀ и ϑ зафиксированы, u – s -мерный вектор управления, v – r-мерный вектор помехи, P и Q – компакты, символ |x| – обозначает евклидову норму вектора x.

Функцию f полагаем непрерывной по t, u, υ и в каждой ограниченной области G пространства {x} удовлетворяющей условию Липшица по x с константой L_G, т.е.

|f(t, x⁽¹⁾, u, υ) - f(t, x⁽²⁾, u, υ)|≤

≤L_G|x⁽²⁾-x⁽¹⁾|,

где x⁽ⁱ⁾∈ G, i = 1,2.

Предполагается, что выполняется условие седловой точки для маленькой игры [7], то есть

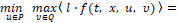
 (2)

где l – любой n – мерный вектор, символ ⟨l⋅f(t, x, u, υ)⟩ – обозначает скалярное произведение векторов в пространстве Rⁿ.

Критерий качества процесса управления. В качестве критерия, определяющего цель управления игроков, будем рассматривать некоторый функционал, зависящий от движения объекта на всём отрезке времени управления, называемый позиционным [2, 3].

γ=γ(x[t],t₀≤t≤ϑ).   (3)

В рамках концепции антагонистических дифференциальных игр [1-9] здесь рассматривается задача на минимакс заданного критерия качества (3), то есть о выборе в схеме обратной связи [3, 9] управлений минимизирующих и выборе помех максимизирующих величину критерия (3).

Оптимальные стратегии. Экстремальный сдвиг. Известно, что при выполнении условия (2) для функции f (1) задачу можно решать в классе чистых позиционных стратегий [2, 3, 6, 9].

u(t_i^(u),x[t_i^(u)],ε_u) ∈ P, i=1,...,ku, 

υ(t_i^(υ),x[t_i^(υ)],ε_υ) ∈ Q, i=1,...,kυ, 

т.е. рассматривается следующая схема управления [3, 9] (рис. 1).

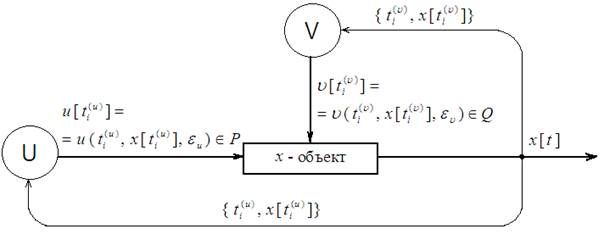
 Рис. 1. Схема управления по принципу обратной связи

Ниже предлагается некоторый оригинальный и конструктивный метод построения оптимальных стратегий игроков – метод экстремально сдвига на сопутствующие точки, идея которого принадлежит авторам.

Для использования этого метода построения оптимальных управляющих воздействий игроков требуется для выбранного критерия качества (3) и ресурсов управляющих воздействий P и Q в (1) уметь вычислять цену игры [5, 9] для любой возможной позиции {t, x} объекта (1).

ρ⁰(t,x)=ρ_u⁰(t,x)=ρ_υ⁰(t,x),

где

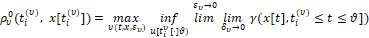
соответственно оптимальные гарантированные результаты первого и второго игроков [3, 5].

Рассмотрим для простоты изложения случай, когда разбиения заданного отрезка времени управления в (1) являются одинаковыми для обоих игроков

t_i+1-t_i≤δ, i=1,…,k,

хотя как видим из схемы управления на рис. 1 они могут быть и различными.

Итак, содержательный смысл метода экстремального сдвига на сопутствующие точки имеет такой вид. Пусть реализовалась позиция

{t_i,x[t_i]}, i=1,…,k-1

объекта (1) в схеме управления по принципу обратной связи (рис. 1).

Окружаем эту позицию шариком достаточно малого радиуса с n-мерными точками w. Далее находим точки, в которых цена игры наименьшая и наибольшая соответственно для первого и второго игроков. Эти точки называем сопутствующими точками. И, наконец, совершаем сдвиг (или первый и второй игрок выбором своих управлений) – пытаемся сдвинуть фазовую точку нашего объекта к своим сопутствующим точкам.

Формально, в математической форме это выражается так.

Выбираем шар K с точками w

K=K(ε)={w∈Rⁿ : |w-x[t_i] ≤ε|,

i=1,…,k-1. 

Находим сопутствующие точки игроков, удовлетворяющие условиям

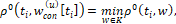
i=1,…,k-1, 

i=1,…,k-1.

Строим n-мерные векторы

и выбираем управления

u₀[t] = u⁰[t_i] = u⁰(t_i,x[t_i],ε), υ[t] = υ⁰[t_i] = υ⁰([t_i], x[t_i],ε), t_i ≤ t ≤ t_i+1,

исходя из условий

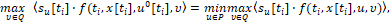
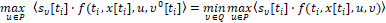
Совершаем указанный экстремальный сдвиг на сопутствующие точки.

Рис. 2. Экстремальный сдвиг

Аналогично плану доказательства из работ [5, 6, 9] устанавливается, что стратегии, построенные методом экстремального сдвига, являются оптимальными в позиционной дифференциальной игре для объекта (1) с критерием качества (3).