Явление хаотической синхронизации было открыто в середине 80-х годов прошлого века. Вид простейшей схемы синхронизации двух хаотических систем представлен на рис. 1.
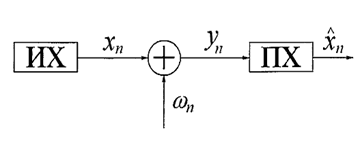
Рис. 1. Схема синхронизации: ИХ – источник хаоса; ПХ – приемник хаоса;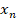 
– хаотический сигнал; 
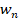– шум; 
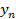– сигнал на входе приемника; 
– сигнал на выходе приемника
В ней предполагается непосредственное воздействие физического процесса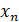 
ведущей системы – источника хаоса (ИХ) на физический процесс ведомой системы – приемника хаоса (ПХ), при наличии в общем случае шума 
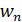в канале [1]. Сигнал на входе ведомой системы имеет вид
.
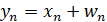Физический процесс на выходе ведомой системы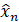 
представляет собой оценку сигнала 
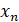на выходе ведущей системы.
Одним из факторов, препятствующих практическому применению хаотической синхронизации, является ее высокая чувствительность к шумам и другим возмущающим воздействиям [5]. Фундаментальной причиной такой чувствительности является наличие информации в самом хаотическом сигнале. Существуют методы синхронизации, в которых от ведущей системы к ведомой передается не сам хаотический сигнал, а информация о нем, достаточная для его восстановления в ведомой системе [2]. В качестве передаваемой информации о хаотическом сигнале может использоваться символическая последовательность. Эта последовательность соответствует "символической" динамической системе, которая эквивалентна исходной хаотической системе, в том смысле, что по ее траектории возможно однозначное восстановление исходных хаотических последовательностей.
Выберем в качестве хаотической системы несимметричное тент-отображение, когда μ≠12. Рассмотрим двоичное представление переменной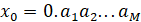 
. В качестве примера выберем 
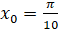и перепишем его в виде x0=0.01010000011000000000. Проследим за преобразованием 
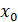при применении к нему отображения
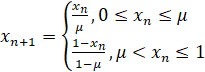(1)
в случае μ=0.7. Серия отсчетов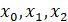 
имеет следующий вид
x0=0.010100000110(00000000),
x1=0.01110010110100100100,
x2=0.10100100000001111100.
Таким образом, действие отображения (1) на начальное условие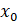 
в случае 
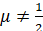приводит к отображению информации об 
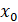, а также обо всех последующих значениях отсчетов, не только в старшие разряды мантиссы, но и в младшие [3]. Однако, при расчетах с конечной точностью, возмущения в младших разрядах не учитываются, что приводит в процессе итерирования к потере части информации о состоянии системы. Это означает, что в несимметричном случае вероятность ошибочной идентификации состояния ведущей системы даже в отсутствии шумов не равна нулю.
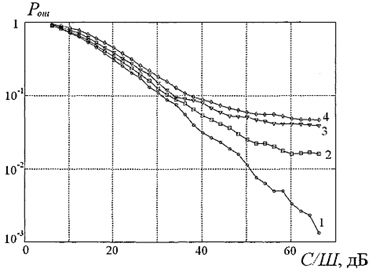
Рис. 2. Вероятность ошибочного восстановления ведущей системы.
Кривая 1 – μ = 0.5, кривая 2 – μ = 0.6, кривая 3 – μ = 0.7, кривая 4 – μ = 0.8
Вероятность ошибочного восстановления состояния ведущей системы Pош зависит от значения параметра μ (рис. 2). Из графика на рис. 2 видно, что чем больше параметр μ отличается от значения 1/2, тем выше вероятность ошибочной идентификации состояния ведущей системы.
Сформулируем алгоритм синхронизации на основе информации о состояниях ведущей системы для несимметричного тент-отображения. На вход ведомой системы с выхода ведущей системы поступает последовательность зашумленных в канале отсчетов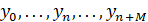 
. В приемнике с помощью обратного итерирования по последовательности 
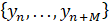, где М - точность вычисления компьютера, происходит восстановление значения 
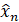. Для того, чтобы проверить является ли восстановленное значение 
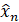точным состоянием ведущей системы 
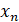и, следовательно, произошла ли точная синхронизация, запускается процесс итерирования идентичный процессу итерирования, происходящему в ведущей системе, с начальным значение 
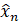. Если через М итераций значения отсчетов последовательносте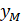й 
и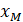 
разойдутся на величину большую уровня шума в канале σ, то восстановленное значение 
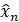не будет являться точным значением состояния ведущей системы 
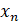и процесс вхождения в синхронизацию должен быть повторен для следующего значения состояния ведущей системы 
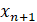. В противном случае пара ведущая-ведомая система является синхронизованной.
В [4] предложен подход к очистке хаотического сигнала, согласно которому выбор ветви при обратной итерации текущего состояния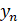 
проводится на основе самого значения предыдущего отсчета 
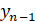. Используем данный подход для построения алгоритма восстановления точного состояния ведущей системы.
Пусть в качестве хаотического источника используется тент-отображение (1) и точность вычислений ограничена М битами. На вход приемника поступает последовательность зашумленных отсчетов. Для восстановления n-го состояния ведущей системы воспользуемся обратным тент-отображением
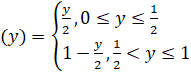(2)
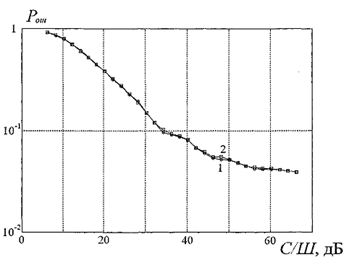
Рис. 3. Вероятность ошибочного восстановления ведущей системы для разных алгоритмов при μ = 0.7
Восстановление начнем с отсчета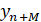 
. На первом шаге из двух прообразов точки 
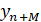выбираем тот, который ближе к отсчету 
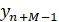и обозначим его 
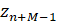. На втором шаге из двух прообразов отсчета 
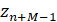выбираем тот, который ближе к 
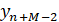и обозначаем его 
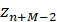. Процесс продолжается до получения отсчета 
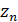, который и рассматривается в качестве восстановленного значения состояния ведущей системы 
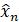. Остается определить произошла ли синхронизация. Подействуем отображением (1) на восстановленное значение 
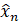и через М итераций сравним значения отсчетов 
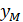и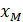 
. Если имеет место выражение
,
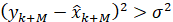то при синхронизации произошла ошибка и процесс восстановления необходимо повторить для другого состояния системы. В противном случае пара ведущая-ведомая система является синхронизованной.
На рис. 3 приведена зависимость вероятности ошибочной идентификации состояния Pош от отношения сигнал шум в канале для описываемого подхода в сравнении с предыдущим алгоритмом при μ=0.7. Из графика видно, что и первый и второй алгоритмы дают приблизительно одинаковые результаты по вероятности точной синхронизации.
