Для того, чтобы при реконструкции сигнала не было искажений необходимо иметь ортогональные симметричные и антисимметричные вейвлеты. В научной литературе отмечается, что таких вейвлетов не существует. При синтезе цифровых фильтров также желательно иметь симметричные и антисимметричные импульсные характеристики, так как это обеспечивает одинаковую временную задержку для всех частот сигнала. Такие фильтры имеют импульсную характеристику конечной длины (КИХ-фильтры). Применение таких фильтров приводит для прямоугольных амплитудно-частотных характеристик (АЧХ) к пульсациям слева и справа от частоты среза и появлению переходной полосы (явление Гиббса). Объясняется это усечением ряда Фурье. Чем короче ряд, тем в большей степени происходит отклонение частотной характеристики от первоначальной на крутых перепадах. Объясняют явление Гиббса еще используя свойство свертки. Произведение функции, с бесконечно длинной импульсной характеристикой, на функцию окна конечной длины, в частотной области соответствует свертке их Фурье-образов. Для прямоугольного окна Фурье-образом является sinc-функция, которая имеет тем более широкий центральный пик для более коротких окон. Если Фурье-образом импульсной характеристики является передаточная функция (частотная характеристика) с прямоугольной АЧХ, то ее свертка с sinc-функцией порождает явление Гиббса. Для уменьшения пульсаций применяются различные виды окон (весовые функции). Также в научной литературе по цифровым фильтрам, на основе критерия Пэли–Винера (Пели–Виннера) доказывается, что фильтры с прямоугольной АЧХ физически нереализуемы.
Насколько цифровой фильтр (вейвлет) подходит для практического применения можно проверить, декомпозируя сигнал прямым и реконструируя обратным вейвлет-преобразованием (ВП). Если реконструированный сигнал точно совпадает с оригинальным сигналом, то вейвлет уверенно использовать на практике. Основным признаком вейвлетов являются нулевое среднее. Нулевое среднее означает, что график функции должен осциллировать (быть знакопеременным) вокруг нуля на оси времени и иметь нулевую площадь:
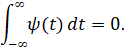
Часто для приложений необходимо, чтобы все первые n моментов были равны нулю:
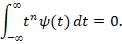
Вейвлеты n-го порядка позволяют анализировать более тонкую (высокочастотную) структуру сигнала, подавляя медленно изменяющиеся его составляющие. Для получения вейвлетов n-го порядка были проведены исследования [1, с. 27; 2, с. 50; 3] и были сконструированы ортогональные симметричные и антисимметричные вейвлеты с прямоугольной АЧХ. На рис. 1 представлена пятая часть ортогонального симметричного вейвлета n-го порядка. Чем больше первых нулевых моментов у вейвлета для данного масштабного коэффициента, тем более уже эффективная ширина спектра. В теории обобщенного ПФ доказывается, что вейвлеты ортогональны, если скалярное произведение вейвлетов с разными масштабными коэффициентами равно нулю. Исследования показывают, чем меньше наложение спектров вейвлетов для разных масштабных коэффициентов, тем меньше скалярное произведение этих вейвлетов.
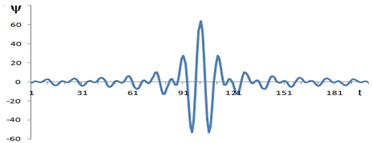
Рис. 1. Ортогональный симметричный вейвлет
На рис. 2 представлена АЧХ этого вейвлета в децибелах. Видно, что в полосе задержания ослабление около -300 дБ, что сравнимо с погрешностью вычисления.
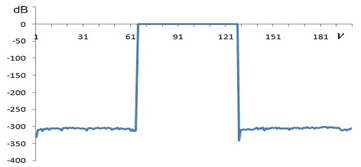
Рис. 2. АЧХ симметричного вейвлета
Например, при скалярном произведении синусоид с разными частотами с числом отсчетов, как у данных вейвлетов, вычисленное значение больше -300 дБ. На самом деле скалярное произведение должно быть равно нулю, так как синусы и косинусы образуют ортонормированный базис. Вычисления показывают, что скалярное произведение сконструированных вейвлетов равно нулю. Такое наблюдается для всех скалярных произведений вейвлетов с другими масштабными коэффициентами. Только скалярные произведения вейвлетов с одинаковыми масштабными коэффициентами не равны нулю. Вид АЧХ симметричных и антисимметричных вейвлетов не зависит от размера (длины) вейвлета, т.е. независимо от размера вейвлета переходной полосы нет. Можно сказать, что вейвлеты имеют идеальную АЧХ в пределах погрешности вычисления. Если в критерии Пэли-Винера
модуль частотной передаточной функции не равен нулю, но меньше погрешности вычисления, то интеграл не расходится. В связи с этим, можно сказать, что сконструированные вейвлеты не противоречат критерию Пели–Винера. А явление Гиббса не наблюдается. Объяснить это можно, если представить вейвлет конечной длины произведением вейвлета конечной длины на окно бесконечной длины. Тогда в частотной области будет свертка Фурье-образа вейвлета с дельта-функцией. Если Фурье-образ вейвлета передаточная функция с прямоугольной АЧХ, то ее свертка с дельта-функцией не порождает явление Гиббса.
Сконструированные вейвлеты применялись для декомпозиции и реконструкции сигналов. Для количественного сравнения использовалась мера типа корреляции между реконструированным сигналом и оригинальным сигналом. Вычисленное значение коэффициента корреляции Пирсона сигнала и реконструированного сигнала равнялось 0,99999 для многих исследований.
Вычисление непрерывного ВП прямым численным интегрированием для больших временных последовательностей занимает длительное время. Для увеличения быстродействия разработаны алгоритмы непрерывного быстрого ВП с использованием быстрого преобразования Фурье (БПФ). Разработанные алгоритмы позволили уменьшить время вычисления ВП на четыре порядка по сравнению с прямым численным интегрированием для вейвлетов на основе производных функции Гаусса при большой выборке сигнала. Алгоритмы прямого и обратного непрерывного ВП представлены в работах [4, 5]. Вейвлеты с прямоугольной АЧХ позволили уменьшить время вычисления прямого ВП в частотной области в 2 раза по сравнению, когда использовались вейвлеты на основе производных функции Гаусса. Также такие вейвлеты позволили уменьшить время вычисления обратного ВП сигнала с размером выборки 32768 и 262144 отсчетов в 260 и 5000 раз соответственно по сравнению с алгоритмом с использованием БПФ. Конструирование симметричных и антисимметричных вейвлетов с прямоугольной АЧХ позволило обратное ВП вычислять во много раз быстрее, чем с использованием БПФ. По сравнению с прямым численным интегрированием вейвлеты с прямоугольной АЧХ позволили уменьшить время вычисления обратного ВП на семь порядков. Профилировка проводилась для процессора Celeron® с частотой 2,54 Ггц, ОЗУ 1 Гб.

.png&w=640&q=75)