В современных условиях развития электроники большую важность занимает вопрос фильтрации сигнала из шума. Традиционные методы фильтрации такие как КИХ, БИХ фильтры обладают ограничениями при очень низких отношениях сигнал-шум. Альтернативным вариантом является метод накопления. Особенность метода – способность подавлять некоррелированный шум при сохранении периодической составляющей.
Метод накопления основан на фундаментальном свойстве аддитивного белого гауссовского шума (АБГШ): при суммировании N реализаций сигнала мощность полезного сигнала растет как N², а мощность шума – лишь как N. Докажем это.
Пусть каждый отсчет наблюдаемого сигнала представляет собой (1):
![]() , (1)
, (1)
Где:
![]() – полезный сигнал$.
– полезный сигнал$.
![]() – АБГШ (независимые реализации).
– АБГШ (независимые реализации).
При суммировании N периодов сигнала получим (2), предполагая, что xi представляет собой один полный период:
| (2) |
Тогда мощность полезного сигнала в аддитивной смеси после суммирования будет равна (3):
![]() , (3)
, (3)
А мощность шума (4) после суммирования:
| (4) |
Таким образом, отношение сигнал шум после суммирования возрастает в N раз (5):
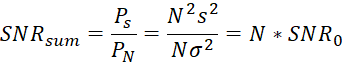 , (5)
, (5)
Оценку сигнала после использования метода накопления можно записать в следующем виде (6):
| (6) |
Проведем моделирование метода накопления в MATLAB. Для этого необходимо создать полезный сигнал и шум, получить их аддитивную смесь и осуществить сам метод накопления, то есть сложить N периодов сигнала.
В качестве полезного сигнала выберем прямоугольный (рис. 1).
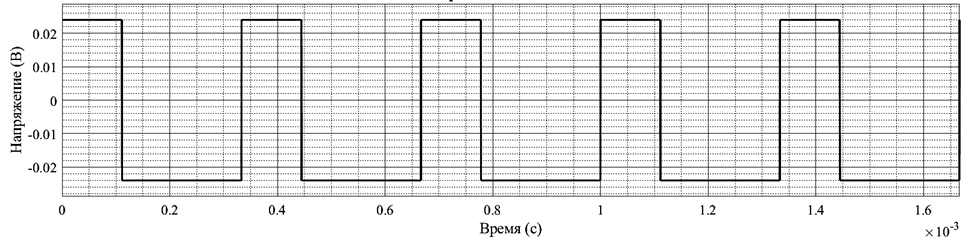
Рис. 1. Периодический прямоугольный сигнал
Далее создадим гауссовский шум с нулевым математическим ожиданием и среднеквадратическим отклонением, равным амплитуде полезного сигнала. Полученный шум праведен на рисунке 2.
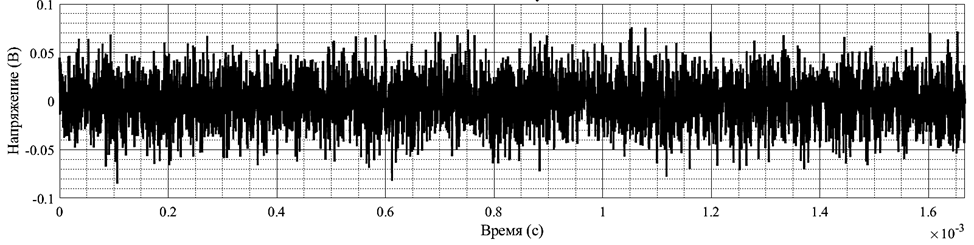
Рис. 2. Белый шум с нормальным распределением
В результате сложения этих сигналов получится следующая аддитивная смесь сигнала и шума (рис. 3).
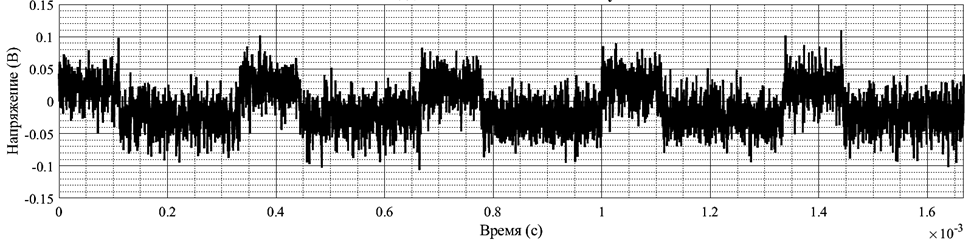
Рис. 3. Аддитивная смесь прямоугольного сигнала и белого шума
В результате использования метода накопления с разными периодами накопления N были построены сигналы (рис. 4).
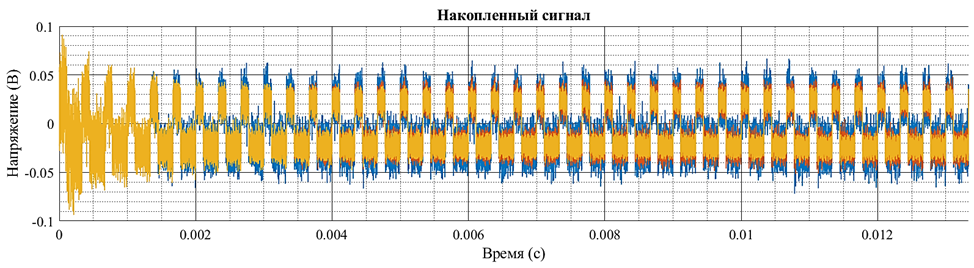
Рис. 4. Результаты метода накопления: синий график –N=4, красный график – N=10, желтый график – N=20
Результаты показали, что с увеличением количества периодов накопления отношение сигнал-шум улучшается. В начале процесса накопления отношение сигнал-шум быстро растет. Это особенно заметно на первых 5–20 циклах, где каждый новый период дает значительное улучшение SNR. Однако по мере увеличения N рост SNR замедляется, поэтому существует оптимальное число циклов накопления, после которого дальнейшее увеличение N не приводит к существенному улучшению сигнала. Для более эффективной обработки целесообразно комбинировать метод накопления с другими алгоритмами фильтрации, учитывающими нестационарность сигналов и шумов.
Основные преимущества рассмотренного подхода заключаются в его способности значительно улучшать SNR при относительно простой реализации. Метод демонстрирует хорошую универсальность для различных типов периодических сигналов, что делает его ценным инструментом в задачах цифровой обработки.
Однако следует учитывать существующие ограничения. Эффективность способа существенно снижается при работе с нестационарными сигналами или в условиях коррелированного шума. Также для достижения качественных результатов требуется значительное количество реализаций, что может быть ресурсозатратно.
Проведенное исследование подтвердило эффективность метода накопления для выделения периодических сигналов из смеси с белым шумом. Результаты моделирования в MATLAB показали, что при увеличении количества суммируемых периодов отношение сигнал-шум улучшается в соответствии с теоретическими расчетами.
.png&w=384&q=75)
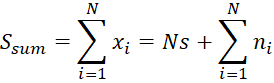 ,
,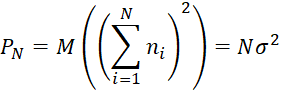 ,
,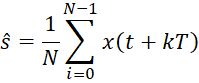 ,
,.png&w=640&q=75)