Ведение. Рассматривается задача [1-13] о построении блока взаимного устойчивого отслеживания реального динамического нелинейного объекта и его компьютерной (виртуальной модели-лидера (поводыря). Задача решается в условиях дефицита (неполной информации о действующих на объект динамических помехах. Кроме того рассматривается случай когда информации о позиции объекта в каждый текущий момент времени в схеме управления по принципу обратной связи поступает с искажением (неточность или ошибка в измерении), что вообще говоря, соответствует реальной ситуации позиционного управления. Рассматривается случай когда нелинейная по управлению и помехе функция f(…) не удовлетворяет так называемому условию седловой точки в маленькой игре [12]. Поэтому задача взаимного отслеживания движений объекта и модели-поводыря решается в классе смешанных стратегий, т.е. используется некоторый вероятностны механизм формирования управлений для объекта и модели. Однако, доказывается что при этом близость движений на всем отрезке времени управления обеспечивается (гарантируется) с вероятностью сколь угодно близкой к единице. Такие задачи отслеживания движений реального объекта и его компьютерной модели занимают достаточно большое место среди задач управления в технике, экономике и т.д. Задача решается в рамках концепции, разрабатываемой в уральской школе по оптимальному управлению и дифференциальным играм Н.Н. Красовского [6, 12]. Для построения оптимальной стратегии управления, используется метод экстремального сдвига [2, 3], предложенный автором. Задача докладывалась в пленарном докладе автора на международной конференции в октябре 2020 года [13].
Управляемый объект. Рассматривается объект, движение которого описывается обыкновенным векторным нелинейным дифференциальным уравнением
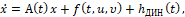
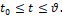(1)
Здесь x – n-мерный фазовый вектор управляемого объекта; t – время, моменты времени начальный t0 и конечный ϑ зафиксированы; u – r-мерный вектор вектор управления, υ – s-мерный вектор помехи. Точка над буквой обозначает производную по времени.
Вектор управления и вектор помехи стеснены условиями
(2)
В уравнении (1) n-мерный вектор некоторой действующей на управляемую систему случайной динамической помехи (шума), про которую нам известно лишь, что она ограниченагде P и Q – ограниченные замкнутые множества векторов, т.е. – компакты. Они определяют ресурсы соответственно управляющего органа U и органа V, вырабатывающего помехи в схеме управления по принципу обратной связи (рис. 1).
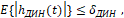
где символ E{…} – математическое ожидание [8].
Кроме того в рамках концепции екатеринбургской школы по оптимальному управлению и дифференциальным играм рассматривается такая задача, когда помеха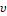 
- и правило (стратегия), по которому она формируется в схеме управления по принципу обратной связи [1-13] (рис. 1).
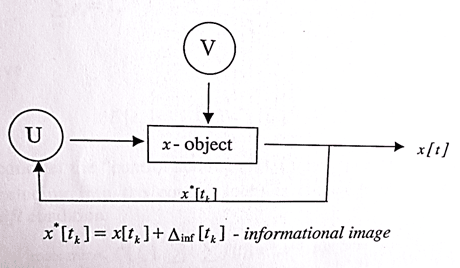
Рис. 1. Обратная связь
На рис. 1
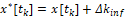
информационный образ и Δinf
случайная информационная ошибка, такая, что в каждый момент времени
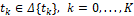
мы знаем только искаженную позицию (рис. 2)
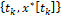
и ограничения на ошибку
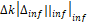
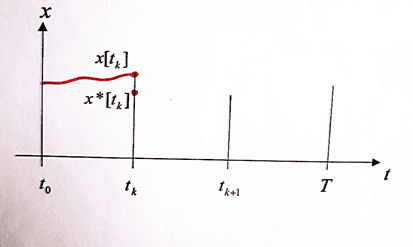
Рис. 2. Информационная ошибка
Рассмотрим случай, когда выполняются условия
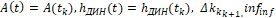
Кроме того, рассмотрим случай, когда множества P, Q (2) являются конечными наборами векторов управлений и помех, т.е.
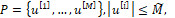
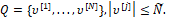
В таком случае рассмотрим х-объект (1), (2), описываемый дифференциально-разностным уравнением
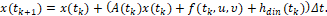(3)
Модель-лидер. Для x-объекта (3) рассмотрим следующую z-модель-лидер (поводырь)
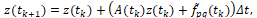(4)
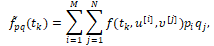где
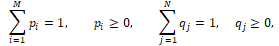
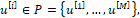
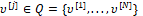
И вектор-функция f и множества P, Q те же, что и для х-объекта (3).
Конструкции управлений для х-объекта и z-модели. Укажем способ формирования правлений u для х объекта, основанный на некотором вероятностном механизме и «управлений» q для z-модели, обеспечивающий близость движений объекта и модели на всем отрезке времени управления. Этот способ основан на методе экстремального сдвига [2, 3, 12].
В момент tk мы выбираем вектор
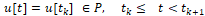
для реального х-объекта (3) с помощью случайного теста с вероятностью [8]
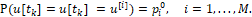
при условиях
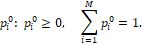
Эти вероятности мы выбираем из так называемого условия минимаксного экстремального сдвига
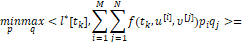
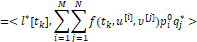(5)
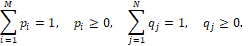
В (5) мы имеем (рис. 3)
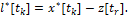
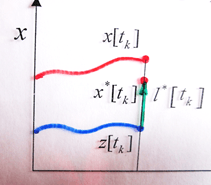
Рис. 3. Экстремальный сдвиг
Далее, пусть «управления» - вероятности
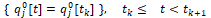
для компьютерной z-модели-лидера выбираются из условия максиминного экстремального сдвига
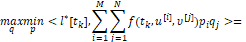
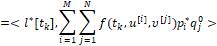(6)
При этом вероятности {qj}, которые определяют стохастические помехи
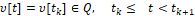
Для х-объекта (3) и “действия” {pi} для z-модели (4) могут быть любыми, удовлетворяющими условиям
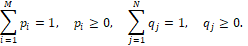
Взаимное отслеживание в комбинированном процессе {x-объект, z-модель-лидер}. Справедлива следующая теорема.
Теорема. При описанном выше выборе (5) и (6) случайного действия u для x-объекта (3) и «действий» q для z-модели (4), для любых выбранных заранее чисел
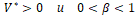
существуют достаточно малые числа
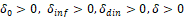
такие, что выполняется следующее неравенство (условие близости)
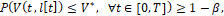(7)
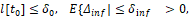если
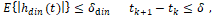
где вt (7)
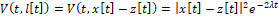(8)
функция Ляпунова, λ>0 – постоянная, ограничивающая норму матрицы A(t) в (1).
Символ l P(…) i в левой части (3) обозначает вероятность [8] всех реализаций движений {x[t],z[t]}, каждое из которых удовлетворяет неравенству
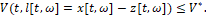
ω обозначает элементарное событие [8], которое принадлежит множеству всех элементарных событий для соответствующих реализаций
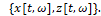
Эта теорема формально означает следующее.
Если мы выбираем в каждый момент времени tk, k=0,…,K управление для объекта (1), (3) как результат случайного испытания из (5), т.е.
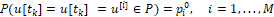
и выбираем для модели (4) набор
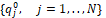
из (6), тогда для каждой возможной помехи
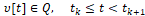
для х-объекта (3) и набора
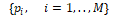
для z-модели (4) будут выполнены следующие условия.
Движения х-объекта (3) и z-модели (4) будут близки (взаимно отслеживать друг друга) в смысле (7), (8) с вероятностью сколь угодно близкой к единице (рис. 4)
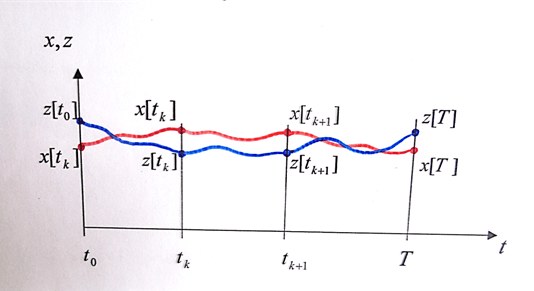
Рис. 4. Близость движений
Идея доказательства этой теоремы опубликована в работах [10, 11, 13].
Заключение. В работе предложена эффективная конструкция блока взаимного отслеживания движений реального динамического нелинейного объекта и его виртуальной модели-лидера. Данная конструкция была опробована на широкомасштабном вычислительном эксперименте для некоторых конкретных механических объектов на плоскости и в трёхмерном пространстве [11].
.png&w=640&q=75)
