Известно, что начало исследований, связанных с аппроксимацией на всей оси, было положено С.Н. Бернштейном, заданной на бесконечном интервале посредством целых функций конечной степени и создал теорию приближения на всей оси R=(-∞,+∞). В работах И.И. Ибрагимова и Ф.Г. Насибова, а также в работе В.Ю. Попова, в которых рассматривается экстремальная задача об отыскании точных констант в неравенствах типа Джексона – Стечкина для наилучших среднеквадратических приближений функций целыми функциями экспоненциального типа. В дальнейшем эта тематика нашла своё развитие в серии работ [2-7]. Полученные в этой статье результаты являются продолжением и развитием цитированных выше работ в этом направлении.
Пусть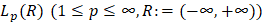 
– пространство измеримых и суммируемых в p-й степени на всей оси R функций f с конечной нормой
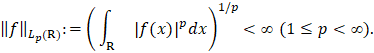
При этом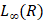 
– пространство измеримых и ограниченных на R функций с нормой
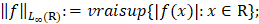– множество натуральных чисел; 
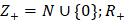– множество положительных чисел вещественной оси. Через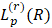
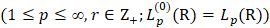обозначим множество функций 
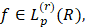у которых производные (r-1)-го порядка 
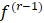локально абсолютно непрерывны, а производные r-го порядка 
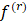принадлежат пространству 
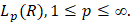Всюду далее, как в [1], структурные свойства функции 
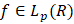характеризуем скоростью стремления к нулю обобщённым модулем непрерывности m-го порядка r-й производной
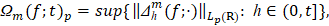
где
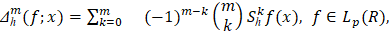
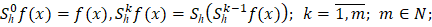
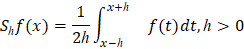
– средние Стеклова функции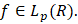 
Символом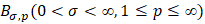 
будем обозначать сужение на R множества всех функций экспоненциального типа σ принадлежащих пространству 
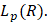Величину
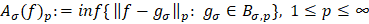
называют наилучшим приближением функции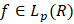 
элементами подпространства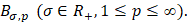 
Введём следующую экстремальную характеристику
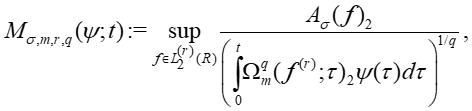
где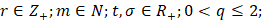 
ψ – неотрицательная измеримая суммируемая на отрезке [0, t] функция, не эквивалентная нулю.
Теорема 1. Пусть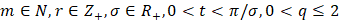 
и ψ – некоторая неотрицательная измеримая суммируемая на отрезке функция, тождественно не равная нулю. Тогда выполняются неравенства
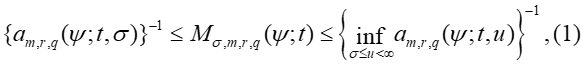
где
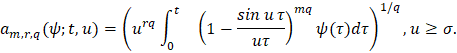
Следствие 1. Пусть выполнены все условия теоремы 1 и, кроме того, весовая функция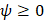 
является суммируемой на отрезке 
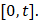Тогда при любом 
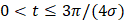справедливо равенство
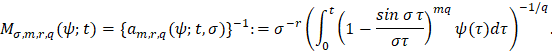
Следствие 2. Если в утверждении следствия 1 полагать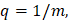 
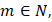
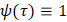
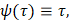то соответственно получаем равенства:
где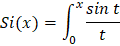 
– интегральный синус;
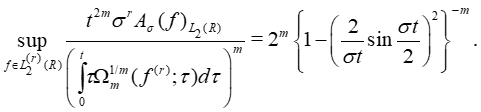
Отметим, что полученные результаты некотором смысле обобщает ранее доказанные теоремы в работах [2, 3].
Известно, что если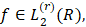 
то все промежуточные производные 
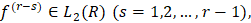а потому представляет несомненный интерес отыскать значение экстремальных характеристик, содержащих величины наилучших приближений промежуточных производных 
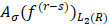вместо величины наилучших приближений 
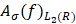элементами 
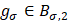в норме пространства Имеет место следующая
Теорема 2. Пусть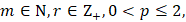 
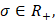
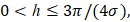
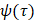– некоторая суммируемая на отрезке 
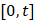функция, тождественно не равная нулю. Тогда имеет место равенство
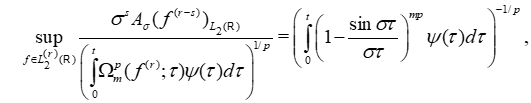
где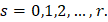 
Используя полученные результаты, нами в работах [4-7], найдены точные значения различных средних -поперечников некоторых классов функций.
.png&w=640&q=75)
