Приближение функций и её производных частными суммами Фурье – Чебышёва В L2,µ[–1,1]

При изучении вопроса разложения функций в рядах Фурье-Чебышёва в гильбертовом пространстве 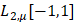 с весом Чебышёва  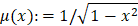вместо обычного модуля непрерывности используется оператор обобщённого сдвига [1]

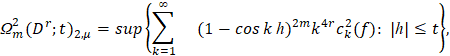
с помощью которого определяются обобщённые модули непрерывности -ых порядков, имеющий вид

и классы функций, которые характеризуются этими модулями непрерывности.

К настоящему времени известен целый ряд содержательных результатов, связанных с отысканием точных констант в неравенстве типа Джексона–Стечкина и вычислением точных значений различных -поперечников функциональных классов (см., например, [1-3]), принадлежащих пространству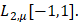 

В этой статье мы продолжим исследования в этом направлении и докажем точные неравенства типа Колмогорова для наилучшего приближения действительных измеримых на отрезке [-1,1] функций 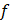 с весом  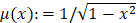 элементами подпространства алгебраических полиномов  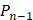в гильбертовом пространстве  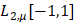с конечной нормой

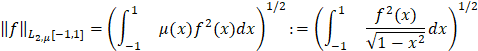
и дадим некоторые eë приложения для решения других экстремальных задач приближения в .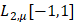

Пусть

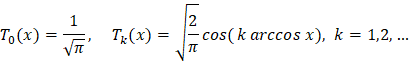(1)

– ортонормированная система многочленов Чебышёва первого рода в пространстве 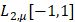. Тогда, как хорошо известно (см., напр., [4, с.91-98]),

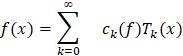(2)

есть ряд Фурье-Чебышёва функции 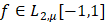, а 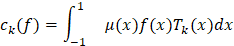 – коэффициенты Фурье–Чебыщёва. Равенство в (2) понимается в смысле сходимости в пространстве 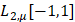. Пусть теперь  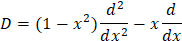 – дифференциальный оператор второго порядка. Операторы высших порядков определим последовательно, полагая  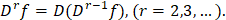 Известно [4, с.54], что многочлены (1) удовлетворяют дифференциальному уравнению

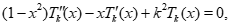(3)

а потому из (3) сразу следуют равенства

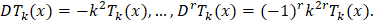
Положим 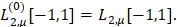  Для 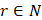 обозначим через  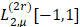 – множество функций 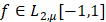, у которых производная  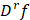принадлежит пространству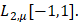 

Для произвольной функции 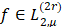 легко получить равенство [1]

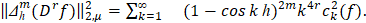   (4)

Учитывая соотношение (4), модуль непрерывности запишем в виде

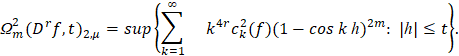(5)

Пусть

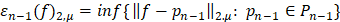  (6)

– наилучшее приближение функции 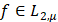 элементами подпространства  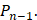В [4, с. 26] доказано, что среди всех элементов  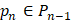частичная сумма

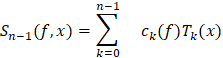
ряда (2) доставляет минимум величине (6). При этом

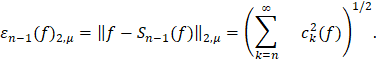
При решении экстремальных задач теории приближений важную роль играют неравенства между нормами последовательных производных функций или неравенства типа Колмогорова [5] в различных банаховых пространствах. Если S = R или S = R₊, то неравенство Колмогорова имеет вид

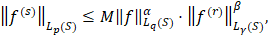  (7)

где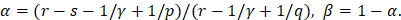  

Отметим, что в работе В.В.Арестова [5] приведён обстоятельный обзор всех результатов неравенства вида (7), где получены наилучшие константы в неравенствах типа Колмогорова и указывается их связь с известной задачи Стечкина о наилучшем приближении неограниченных операторов ограниченными. Поскольку для функции  её промежуточные производные 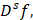 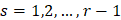 принадлежат пространству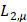, то представляет интерес изучение поведения наилучших приближений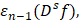 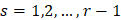   на классе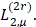 

В [1] доказано, что при любых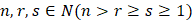 и для произвольной функции  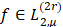справедливо точное на  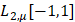неравенство типа Колмогорова

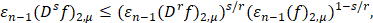(8)

которое обращается в равенство для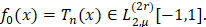 

Через 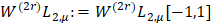 обозначим класс функций 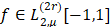,, у которых  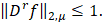 Положим

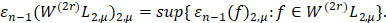
Имеет место следующая

Лемма. Справедливо равенство

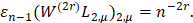
Задача совместной наилучшей полиномиальной приближении функции 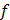 и её последовательных производных  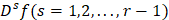 формулируется в следующей постановке: для натуральных чисел  удовлетворяющих условию  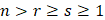требуется найти точное значение величины

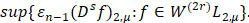(9)

Решение задачи (9) находим как следствие более общей задачи отыскания точной константы в неравенстве типа Колмогорова (8) в пространстве 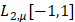. Имеет место следующая

Теорема. При любых  для которых 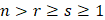  имеет место равенство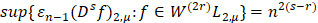  

Используя полученных результатов, можно найти точные значения различных n-поперечников классов функций, определяемых модулем непрерывности (5).