Введение. Рассматривается задача управления по принципу обратной связи конфликтно управляемым нелинейным динамическим объектом [11]. Так как для уравнения движения объекта нелинейного по управлению и помехе не выполняется условие седловой точки для маленькой игры [8]. Известно, что в таком случае задача эффективно решается в классе смешанных стратегий управления [3, 14], то есть используется некоторый вероятностный механизм формирования управлений и помех. Критерий качества процесса управления задаётся в виде некоторого конкретного функционала от движения объекта. Решается задача на минимакс и максимин выбранного критерия качества. При этом гарантированный результат достигается с вероятностью [10] сколь угодно близкой к единице. Особенность рассматриваемой дифференциальной игры заключается в наличии информационных и динамических случайных помех, ограниченных по математическому ожиданию [10]. Задача решается методом экстремального сдвига на сопутствующие точки, разработанным автором [2, 4, 14]. Приводятся результаты численной симуляции рассматриваемого процесса на ЭВМ. При решении задачи также используется блок взаимного отслеживания движений реального объекта и его виртуальной (компьютерной) модели [3, 5, 13, 14].
Управляемый объект. Рассматривается объект, движение которого описывается обыкновенным векторным нелинейным дифференциальным уравнением
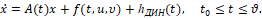 (1)
(1)
Вектор управления u и вектор помехи υ стеснены условиямиЗдесь x – n-мерный фазовый вектор управляемого объекта; t – время, моменты времени начальный t0 и конечный ϑ зафиксированы; u – r-мерный вектор управления, υ – s-мерный вектор помехи. Точка над буквой обозначает производную по времени.
u ∈ P, υ ∈ Q, (2)
где P и Q – ограниченные замкнутые множества векторов, т.е. – компакты. Они определяют ресурсы соответственно управляющего органа U и органа V, вырабатывающего помехи в схеме управления по принципу обратной связи (рис. 1).
В уравнении (1) hДИН – n-мерный вектор некоторой действующей на управляемую систему случайной динамической помехи (шума), про которую нам известно лишь, что она ограничена
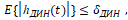
где символ E{…} – математическое ожидание [10].
Кроме того в рамках концепции екатеринбургской школы по оптимальному управлению и дифференциальным играм рассматривается такая задача, когда помеха υ – и правило (стратегия), по которому она формируется в схеме управления по принципу обратной связи (рис. 1).
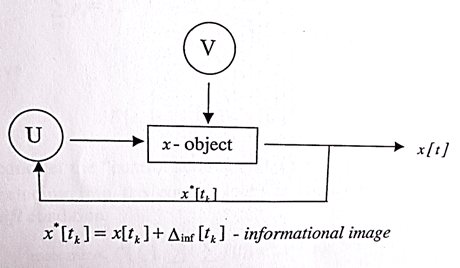
Рис. 1. Обратная связь
На рис. 1 информационный образ [3, 6], где Δinf – случайная информационная ошибка, такая, что в каждый момент времени
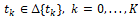
мы знаем только искаженную позицию (рис. 2) 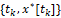 .
.
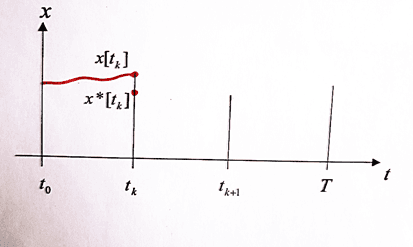
Рис. 2. Информационная ошибка
и ограничения на ошибку
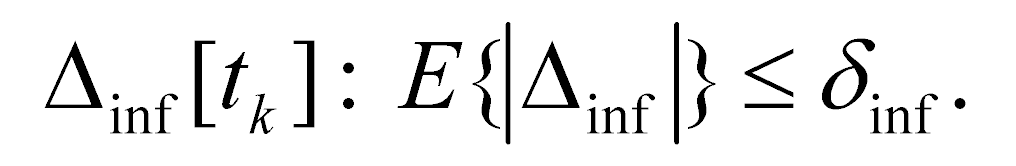
Рассмотрим случай, когда выполняются условия
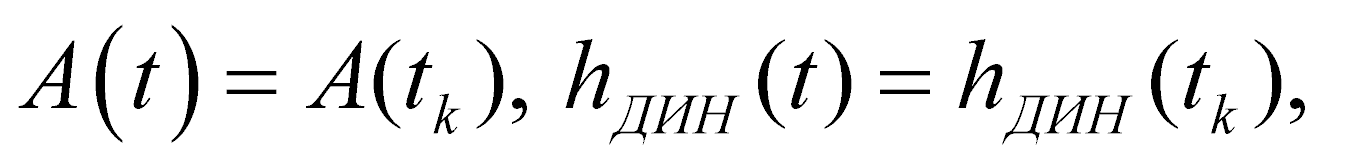
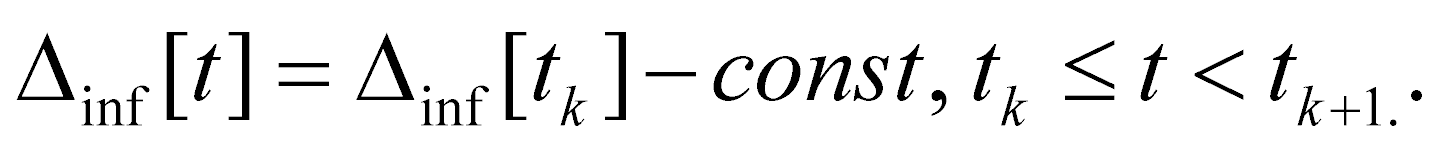
Кроме того, рассмотрим случай, когда множества P, Q (2) являются конечными наборами векторов управлений и помех, т.е.
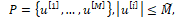
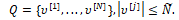
В таком случае рассмотрим х-объект (1), (2), описываемый дифференциально-разностным уравнением [3, 5, 13]
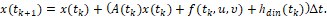 (3)
(3)
Рассмотрим одну конкретную конфликтно-управляемую динамическую систему вида (3). А именно – систему вида
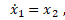
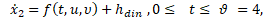
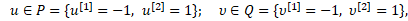 (4)
(4)
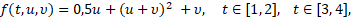
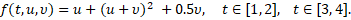
Такая нелинейная система не удовлетворяет так называемому условию седловой точки для маленькой игры [8], т.е. – условию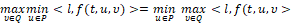
для любого двумерного вектора l.
Известно, что в таком случае задачу эффективно решать в классе смешанных стратегий [2, 3, 11, 14].
Критерий качества. Рассмотрим следующий конкретный критерий качества [2, 14, 15] процесса управления
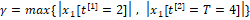
и в рамках концепции антагониститческой дифференциальной игры двух лиц (игроков) [1-7; 9; 11-15] рассмотрим задачу о конструировании управлений, минимизирующих критерий качества и о формировании помех, максимизирующих его, т.е.
1 игрок: 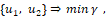
2 игрок: 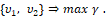
Такая задача рассматривалась и была представлена автором на пленарном докладе Международной конференции [15]. Решение этой задачи базируется на взаимном отслеживании движений моделей –лидеров первого и второго игроков [3, 5, 12, 13, 15] и на методе экстремального сдвига на сопутствующие точки [2, 4, 14].
Результаты численного эксперимента. Приведем результаты численного моделирования на ЭВМ рассматриваемой конкретной дифференциальной игры при следующих данных
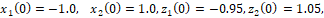
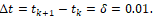
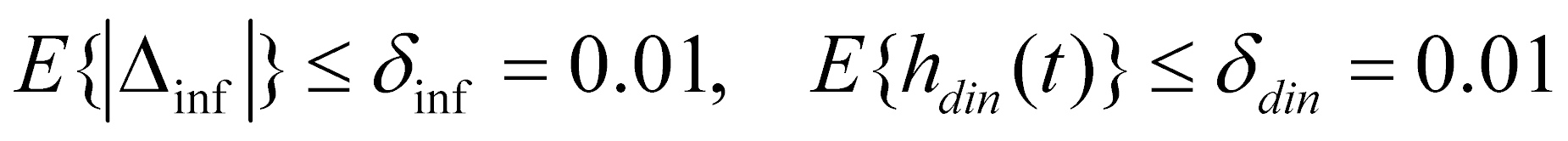
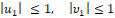
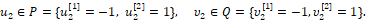
В этом случае получили следующую картину оптимального с точки зрения обоих игроков движения
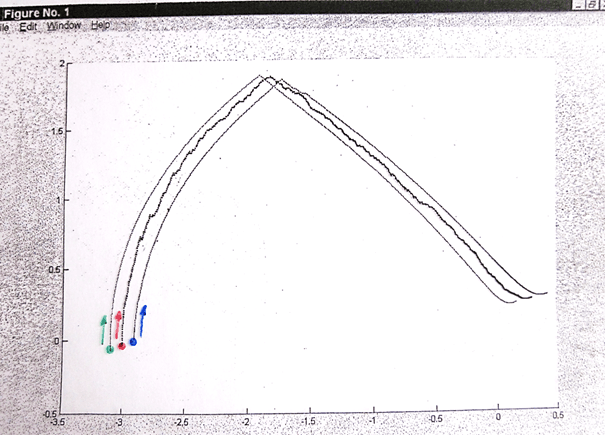
Рис. 3. Картина оптимального процесса
Как видно оптимальное движение объекта (ломанная линия) следует между движениями модели-поводыря первого игрока (нижняя кривая и модели-лидера второго игрока (верхняя линия.
Заключение. В работе приводится одна конкретная дифференциальная антагонистическая игра двух лиц. При решении этой игры используется метод управления по принципу обратной связи в классе смешанных стратегий [3, 14]. Результаты численного эксперимента достаточно хорошо иллюстрируют применяемую теорию, разработанную автором в работах [2, 4, 14].

.png&w=640&q=75)