Введение. Рассматривается некоторая упрощенная математическая модель движения дрона-квадрокоптера [1-4, 6, 10] под действием некоторых выбранных управляющих воздействий. При этом в качестве таких воздействий выбираются угловые скорости вращения винтов. Каждый из четырех винтов снабжен своим электродвигателем и, следовательно, скорости вращения всех винтов могут быть различными. Предлагается и обосновывается некоторая новая модификация математической модели полета в форме дифференциальных уравнений Ньютона-Эйлера [7]. Рассматривается оптимизация движения полета по критерию качества процесса управления [4, 9], определяющего затраты энергии на выработку управляющих воздействий на заданном зафиксированном отрезке времени. При этом за этот отрезок времени дрон совершает перелет из заданного начального в заданное конечное состояние в трехмерном евклидовом пространстве. Математически рассматриваемый критерий качества есть интеграл от квадрата четырехмерного вектора управляющего воздействия, что традиционно для двигателей малой тяги, применяемых, в частности, в авиационной и ракетной технике. Решается задача программного управления [1, 4, 5], при котором оптимальное управляющее воздействие получается в виде некоторой функции времени на заданном отрезке полета квадрокоптера. Отрезок времени управления движением квадрокоптера определяется ресурсом его аккумулятора. Приводится иллюстрирующий пример облёта дроном сельскохозяйственного угодья. При этом в качестве дрона рассматривается конкретный лёгкий квадрокоптер. Особое внимание уделяется предлагаемому способу гарантированной посадки дрона в «гнездо» – месту подзарядки аккумуляторной батареи, обеспечивающей полёт. Работа продолжает исследования автора [1-4, 9].
Постановка задачи. Рассматривается задача о составлении математической модели беспилотного летательного аппарата конкретного распространенного легкого дрона-квадрокоптера (рис. 1): в форме обыкновенного линейного векторного дифференциального уравнения. Также рассматривается задача о конструировании программного векторного управляющего воздействия, обеспечивающего полет квадрокоптера в трёхмерном пространстве в декартовой системе координат из заданного начального в заданное конечное состояние за фиксированное время при наличии детерминированной помехи. И наконец, разработка способа, обеспечивающего точное (гарантированное) попадание квадрокоптера в гнездо.
Рис. 1. Квадрокоптер
Решение. Для составления математической модели управляемого движения квадрокоптера (рас. 1) использована следующая расчетная схема (рис. 2) [1-4, 10].
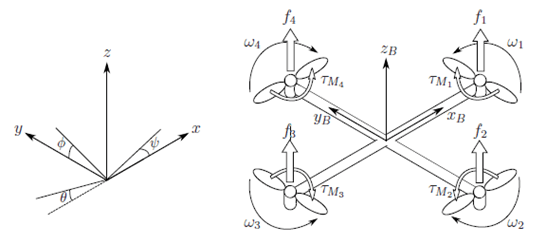
Рис. 2. Расчетная схема квадрокоптера
Здесь ωi, i=1,..., 4 – угловые скорости вращения винтов;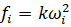 
– силы, создаваемые этими скоростями, где k>0 – постоянный коэффициент, определяемый аэродинамическими характеристиками винта и плотностью воздуха [3]. Управление квадрокоптером как раз и осуществляется с помощью изменения указанных угловых скоростей и создаваемых ими сил. Изменение этих сил подвластно нам, то есть находится под нашим контролем (control – управление, англ.). Таким образом, эти силы и будут играть роль управляющих воздействий, ui, i=1,...,4.
Обозначим:
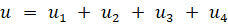
силу тяги, являющуюся объединением сил роторов и являющуюся, таким образом, управлением.
Предлагается следующая упрощенная математическая модель управляемого движения квадрокоптера:
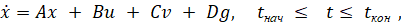
где x – шестимерный вектор:
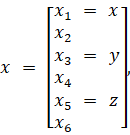
m – масса квадрокоптера, g – ускорение силы тяжести, v сила ветра, А, В, С, D – матрицы:
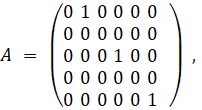
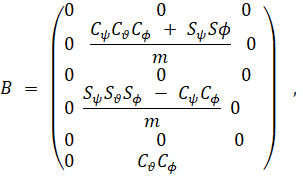
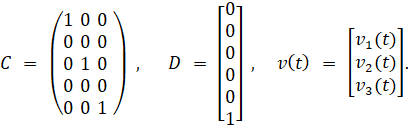
Здесь матрица В выбирается постоянной, т.е. мы полагаем углы Эйлера (рис. 2) постоянными и заданными для рассматриваемого полёта и константы S и С в матрице В определяются соответствующими углами Эйлера [1, 7, 10]. В инерциальной системе отсчета, центробежная сила обнуляется. Таким образом, только гравитационная сила G = mg, величина и направление тяги u и помеха v участвуют в ускорении квадрокоптера.Суть управления параметрами полета заключается в поддержании такого углового положения квадрокоптера, которое обеспечивает его движение (полет) по заданной траектории (а также обеспечивает его зависание в определённые моменты времени). При заданных начальных и конечных условиях:
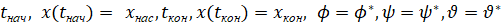
и заданной помехе – силе ветра:
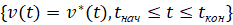
программное управление имеет вид:
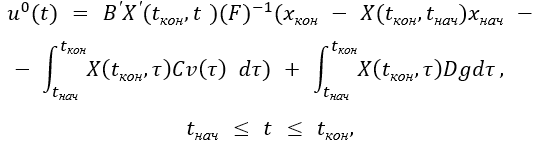
где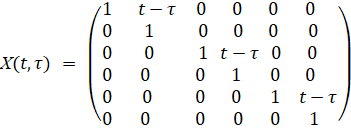 
–
есть фундаментальная матрица [5] для решений однородного дифференциального уравнения:
.
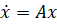Известно, что так сконструированное управление является оптимальным по критерию качества управления [4, 9]:
,
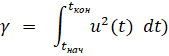характеризующего затраты энергии на выработку управляющего воздействия для двигателей малой тяги, какими можно считать двигатели, рассматриваемого здесь квадрокоптера.
Пример. Рассматривается задача полёта дрона-квадрокоптера – беспилотного летательного аппарата вертолётного типа с четырьмя винтами (рис. 1) по заданной траектории. Винты приводятся в движение каждый своим электродвигателем, питаемым от аккумулятора, включенного в конструкцию дрона.
Рассматривается случай, когда квадрокоптер снабжен аккумулятором небольшой мощности, который разряжается за достаточно малое время (например, 10 минут для квадрокоптера, изображенного на рис. 1). Поэтому требуется подзарядка аккумулятора на старте и финише его движения. В качестве таких зарядных устройств используются так называемые «гнёзда», устанавливаемые на крышах домов, автомобилей, столбов линий электропередач. Рассмотрим следующую схему полёта квадрокоптера для съёмки некоторого объекта сельскохозяйственного угодья (рис. 3).
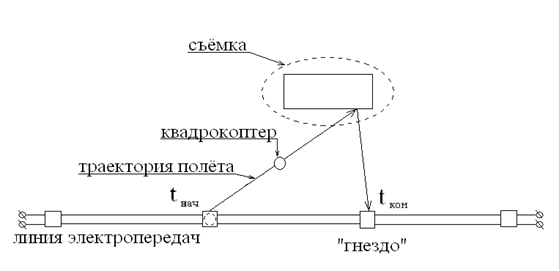
Рис. 3. Схема движения квадрокоптера
Попадание квадрокоптера для зарядки – посадка в «гнездо», представляет определённую трудность, в связи с необходимостью большой точности приземления. Хотя квадрокоптер снабжен видеокамерами, это не упрощает решение такой задачи. В данной работе предлагается некоторый новый способ посадки квадрокоптера в «гнездо», позаимствованный из космической техники – стыковки космических аппаратов [8]. А именно, при стыковке двух космических аппаратов используется трос, который их соединяет и движение происходит благодаря втягиванию троса в один из аппаратов. Это обеспечивает абсолютную точность стыковки. Можно понимать трос, как некоторый «якорь» или «гарпун», который выбрасывает один из объектов (стыкующийся) и попадает в стыковочное отверстие второго аппарата. Такой способ посадки квадрокоптера в «гнездо» и предлагается автором (рис. 4).
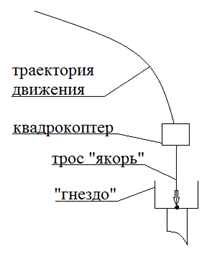
Рис. 4. Посадка квадрокоптера в «гнездо»
Устройство, выбрасывающее и втягивающее трос – «якорь», целесообразно устанавливать в корпусе квадрокоптера, а прицеливание якоря-гарпуна в гнездо осуществлять с помощью видеокамер квадрокоптера.
