Введение. Рассматриваемая задача на минимакс максимин критерия качества, зависящего от движения конкретного механического объекта и реализаций управления и помехи на заданном отрезке времени трактуется как антагонистическая дифференциальная игра двух лиц в рамках концепции екатеринбургской школы по оптимальному управлению Н.Н. Красовского [6, 7, 9]. Работа продолжает исследования авторов [4, 5].
Движение объекта. Рассмотрим точку единичной массы, двигающуюся в горизонтальной плоскости {q1, q2} под действием сил u и υ. Тогда уравнение движения в форме второго закона Ньютона имеет вид
q=u+υ, (1)
P={u: ||u||=(u12+u22)1/2≤2}, u∈P, (2)
где q – двумерный вектор, u и υ – векторные управляющие воздействия, удовлетворяющие условиям:
Q={υ: ||υ||=(υ12+υ22)1/2≤1}, υ∈Q. (3)
Задача. Критерий качества. Рассматривается задача [1-9] об управлениях u и помехах υ, которые соответственно минимизируют-максимизируют величину критерия качества процесса управления [4, 5, 9], заданного в виде функционала
 , (4)
, (4)
где ‹u⋅υ› = u1⋅υ1+u2⋅υ2, ||q[ϑ]|| = (q12[ϑ] + q22[ϑ])1/2, t0≤t*≤ϑ, t0=0, ϑ=2.
Приведем систему (1) к нормальному виду
|
x1=x3 x2=x4 x3=u1+υ1 x4=u2+υ2. |
(5) |
Тогда функционал γ (2) примет вид
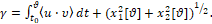 (6)
(6)
В соответствии с известными результатами [3, 4, 7, 9] рассматриваемая дифференциальная игра для системы (5) с функционалом (6) имеет седловую точку {u0(⋅), υ0(⋅)} и цену ρ0(t, x). При этом стратегии u0(⋅)=u0(t, x, ε) и υ0(⋅)=υ0(t, x, ε), составляющие седловую точку, строятся конструктивно по известной цене игры ρ0(t, x). Дифференциальная игра для - объекта (5) с критерием качества γ (6) принимает вид для нелинейного объекта с расширенным фазовым вектором
x={x1,..,x5}
и критерием качества
γ=γ(x[t0[⋅]ϑ] = {x[t], t0≤t≤ϑ|}),
где
|
x1=x3 x2=x4 x3=u1+υ1 x4=u2+υ2 x5=‹u⋅υ› = u1υ1+u2υ2. |
(7) |
Критерий качества γ имеет вид
γ=γ(x[t0[⋅]ϑ]) = ϕ(x[ϑ])+x5[ϑ]. (8)
и критерий качества (9) является позиционным функционалом [5].
Используя метод верхних выпуклых оболочек [9], получаем, что цена ρ0(ti, x[ti]) дифференциальной игры определяется по формуле
ρ0(ti, x[ti]) = ρ0(ti, x[ti])+x5[ti]. (9)
Cогласно [9], имеем
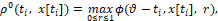 (10)
(10)
где
 (11)
(11)
По известной цене игры ρ0(ti, x[ti]) будем строить стратегии u0(⋅)=u0(t, x, ε) и υ0(⋅)=υ0(t, x, ε) в соответствии с конструкциями экстремального сдвига на сопутствующие точки из работы авторов [4, с. 9].
Пусть реализовалась позиция {ti, x[ti]. В данном примере сопутствующие точки [4, с. 10] будем искать следующим приближенным способом. А именно, вместо того, чтобы искать точки, в которых достигается минимум и максимум цены дифференциальной игры ρ0(ti, x[ti]) в моменты ti, i=1,...,k в схеме управления по принципу обратной связи ([4], рис. 1) при достаточно малом ε>0 будем просто искать точки пересечения с границей области Κ(ε) ([4], рис. 2) вектора градиента su[ti]=[gradxρ0(ti, x)]x[ti] и вектора sυ[ti], противоположного градиенту. При этом, было доказано в [9], что оптимальные стратегии
u0(⋅) и υ0(⋅) от величины x*5 не зависят.
Имеем
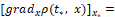
 (12)
(12)
Таким образом, оптимальная стратегия u0(⋅)=u0(t, x, ε) есть правило, которое любой возможной позиции {t*, x*} ставит в соответствие вектор u0={u10, u20} ∈ P (2), удовлетворяющий условию
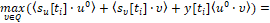
 (13)
(13)
где
su[t]i = r0(ϑ-ti)⋅(x1[ti]+x3[ti](ϑ-ti)) / k[ti],
sυ[ti]=r0(ϑ-ti)⋅(x2[ti]+x4(ϑ-ti)) / k[ti], y[ti]=1, (14)
здесь r0 – максимизирующее значение для (10), и
k[ti]=((x1[ti]+x3[ti](ϑ-ti))2 + (x2[ti]+x4(ϑ-ti))2)1/2. (15)
Оптимальная стратегия υ0(⋅)=υ0(t, x, ε) есть правило, которое любой возможной позиции {t[ti], x[ti]} ставит в соответствие вектор υ0={υ10, υ20} ∈ Q (3), удовлетворяющий условию
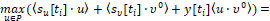
 (16)
(16)
При этом управления u0[ti[⋅]ti+1) = {u0[t] = u0[ti] ∈ P, ti ≤ t≤ ti+1, i=1,…, k} и υ0[ti[⋅]ti+1) = {υ0[t] = υ0[ti] ∈ Q, ti ≤ t ≤ ti+1} определяются следующими формулами:
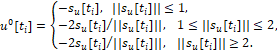 (17)
(17)
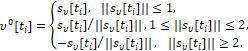 (18)
(18)
В (17) и (18) ti ∈ Δδ{ti}, i=1,…, k+1, где Δδ{ti} разбиение отрезка времени [t0, ϑ] точками ti, так что
ti+1-ti≤δ. (19)
Численный эксперимент. Приводятся результаты численного эксперимента при следующих исходных данных: t*=0, x*1=4.0, x*2=3.0, x*3=2.0, x*4=1.0, ϑ=2.0, δ=0.001. При этих данных цена игры ρ0(t*, x*)=6.601. На рисунке 1 приведена траектория движения объекта при u(⋅)=u0(⋅) и υ(⋅)=υ0(⋅). Здесь получили γ≅ρ0(t*, x*)=6.602. На рисунке 2 – траектория движения при u(⋅)=u0(⋅) и υ[t]={υ1[t]=cosπt, υ2[t]=sinπt}, t* ≤ t ≤ ϑ, т.е. υ(⋅)≠υ0(⋅). Здесь получили γ=6.085<ρ0(t*, x*)=6.601. На рисунке 3 – траектория движения при υ(⋅)=υ0(⋅) и u[t]={u1[t]=2cosπt, u2[t]=2sinπt}, t*≤t≤ϑ, т.е. u(⋅)≠u0(⋅). Здесь получили γ=8.302>ρ0(t*, x*)=6.601.
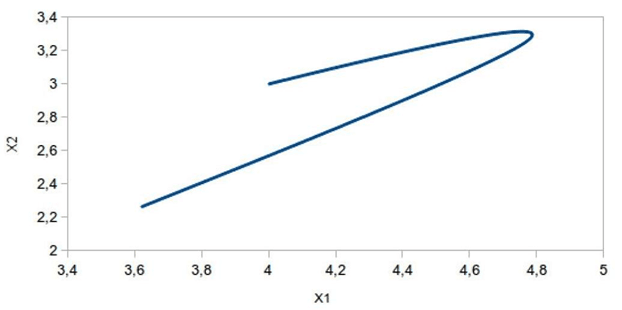
Рис. 1. u – оптимальное, υ – оптимальное
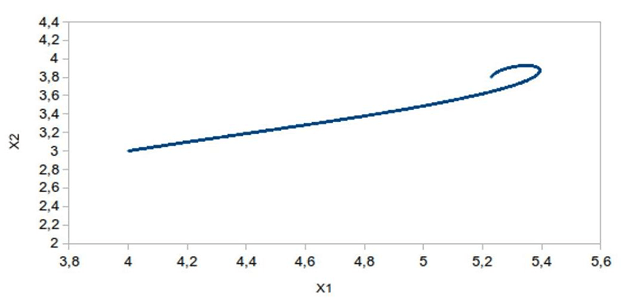
Рис. 2. u – оптимальное, υ1=cos(π t), υ2=sin(π t)

Рис. 3. υ – оптимальное, u1=2cos(π t), u2=2sin(π t)
Результаты проведенного эксперимента полностью согласуются с теорией.

.png&w=640&q=75)