Математическая модель планирующего полёта мяча в футболе со штрафного удара выше «стенки» по вертикальной параболе в «девятку»

Введение. Рассматривается некоторая математическая модель [2-4] движения футбольного мяча после выполнения штрафного удара из-за пределов штрафной площадки команды-соперника.

При этом рассматривается официальный мяч Чемпионата Европы по футболу и учитываются его масса и размеры (рис. 1).

Рис. 1. Официальный футбольный мяч Чемпионата Европы EURO2020

Из дифференциальных уравнений движения в форме Второго закона Ньютона [2, 5, 10], определяющих математическую модель полёта мяча, в рассматриваемом случае исключается сила сопротивления воздуха. Действительно, рассматривая мяч (рис. 1), как шар, двигающийся в воздухе с заданной скоростью, можно обосновать, что эта сила сопротивления будет ничтожно мала (коэффициент сопротивления шара в воздухе достаточно мал) в сравнении с другими параметрами, определяющими полет. Такое обоснование приводится в работе и показывается, что траектории движения шара по параболам в безвоздушном пространстве и в воздухе мало отличаются, и это не влияет на суть рассматриваемой задачи. При этом при полёте мяча в вертикальной плоскости исключается так называемый эффект Магнуса [8], возникающий при закручивании мяча и полёта его в горизонтальной или наклонной к горизонту плоскости. Такие удары имеют место быть в современном футболе. В этом случае мяч летит не над стенкой, а огибает её сбоку. Такие удары выполняет, например, знаменитый португальский футболист Криштиану Роналду (рис. 2).

Рис. 2. Криштиану Роналду

Такие удары мы здесь не рассматриваем. То есть здесь рассматривается так называемый планирующий (без вращения) полёт мяча в вертикальной плоскости, перпендикулярной плоскости площадки футбольного поля (рис. 3).

Рис. 3. Штрафной удар через «стенку» в «девятку»

Известно, что такие полеты мяча имеют место, например, в волейболе при выполнении игроком планирующей подачи.

Поэтому для более точного определения предлагаемой математической модели автор считает целесообразным называть её упрощенной.

Постановка задачи. Удар выполняется только по неподвижно стоящему мячу. Футболист, выполняющий штрафной, должен выполнить удар в одно касание. Пока мяч снова не введен в игру, игроки команды соперника обязаны соблюдать установленную дистанцию, не ближе 9,15 метра от точки, с которой вводится мяч.

На каждой половине футбольного поля размечается штрафная зона. Данная зона необходима для расположения игроков футбольных команд при пробитии штрафного одиннадцатиметрового удара. Размеры стандартной штрафной зоны футбольного поля: 40,32 на 16,5 метра [1] (рис. 4).

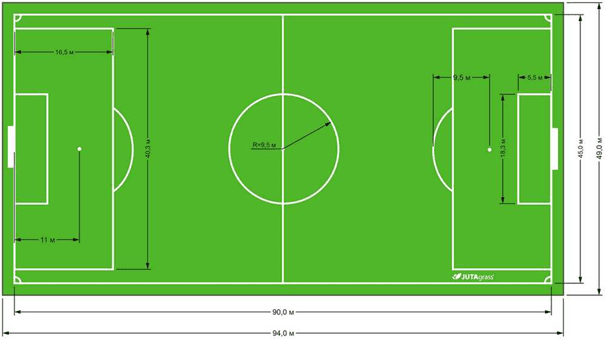
Рис. 4. Размеры футбольного поля

Размеры стандартных футбольных ворот приведены на рис. 5.

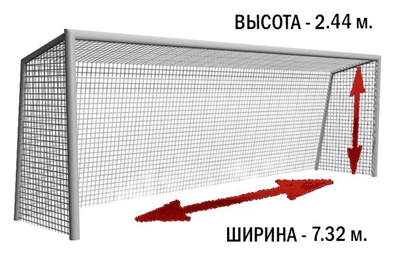
Рис. 5. Размеры футбольных ворот

Таким образом, площадь ворот составляет примерно 17.86 квадратных метров. Площадь ворот делится на зоны равной величины (рис. 6).

Рис. 6. Схема деления ворот на зоны

С учетом размеров ворот (рис. 5), площадь каждой зоны составляет примерно 1,49 квадратных метра. При этом центр зон 9 – «девяток» находится на высоте примерно 2 метра и расстоянии 90 сантиметров слева и справа от соответствующей штанги ворот.

Будем рассматривать случай, когда штрафной удар производится с расстояния 25 метров вне штрафной зоны, и на расстоянии 9 метров от места удара выстроена стенка из игроков противника высотой 2 метра. Требуется произвести штрафной удар так чтобы мяч пролетел над стенкой на высоте большей или равной 2,5 метра (точно не попал в стенку даже при прыжке вверх ее игроков) и попал в левую зону 9 площади ворот (рис. 6), именуемую девяткой (рис. 7).

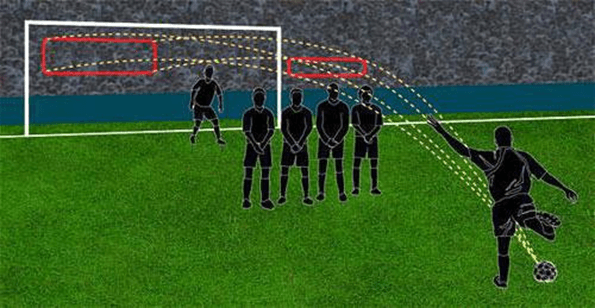
Рис. 7. Траектории полета мяча при штрафном ударе со «стенкой» в «девятку»

Рассмотрим для простоты вычислений случай, когда штрафной удар производится с точки, соответствующей середине штрафной площадки и удар производится в левую девятку без закручивания мяча (планирующий полёт). Для попадания в середину девятки теоретически мяч должен попасть в левую часть ворот на высоте H=2 метра и расстоянии от левой штанги, равном половине длины зоны девятки. Это расстояние равно 0,9 метра. При этом всё сказанное ниже относится и к правой девятке (рис. 6).

Нетрудно проверить, что в этом случае дальность полета мяча до точки попадания в ворота составит l= 25,2 метра и высота в момент пересечения ворот составит Н= 2 метра.

При сделанных допущениях об отсутствии силы сопротивления воздуха для мяча (шара) и отсутствии силы Магнуса, вызываемой вращением мяча, траектория движения буде парабола, которая в осях {XOY} декартовой системы координат имеет вид (рис. 8).

Рис. 8. Траектория планирующего полета мяча

При этом ось Y направляется в точке О – места выполнения штрафного удара вверх, перпендикулярно площадке футбольного поля, а ось X в точке О направлена горизонтально по площадке футбольного поля и пересекает плоскость ворот под некоторым углом на расстоянии 45 см. от левой штанги, т.е. – на расстоянии (как было указано выше) l=25,2 метра, – некоторой части L – длины всей параболы вдоль оси Х (рис. 8).

При этом мяч должен влететь в середину девятки – зоны 9 (рис. 6) на высоте 2 метра – некоторой части максимальной высоты h > 2 метров (рис. 8). Также должно быть выполнено обязательное условие, что на расстоянии 9 метров (х=9) от точки удара мяч должен пролететь над «стенкой» на высоте 2,5 метра (у=2,5). Из всех этих условий мы определяем угол, под которым должен быть произведен удар, и начальную скорость удара по мячу (рис. 8). При этом, во избежание вращения мяча, линия удара должна проходить через точку касания мяча бутсой в момент удара и центром тяжести мяча (рис. 9).

Рис. 9. Удар по мячу

Математическая модель. Известно [9], что размеры официального футбольного мяча (рис. 1) таковы: длина окружности – 68-70 см, вес до 450 г., т.е. принимаем в дальнейших расчетах масса 0,45 кг, диаметр 0,22 м. Ввиду малых размеров мяча по сравнению с расстоянием l=25,2 м., на которое он летит в рассматриваемой модели штрафного удара, будем рассматривать мяч как материальную точку [1, 5], вылетающую из точки О с начальной скоростью 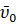, направленной под некоторым углом α ее наклона к горизонту (рис. 8).

Известно [1, 5], что, согласно Второму закону Ньютона [1, 5, 10], законы движения точки (мяча) в рассматриваемом случае при предположениях и допущениях, сделанных выше, имеет вид

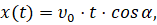
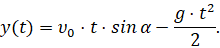    (1)

То есть движение происходит в плоскости {XOY}. Здесь t – время, g=9,8 метра в секунду в квадрате – ускорение силы тяжести Р [1, 5] (рис. 10).

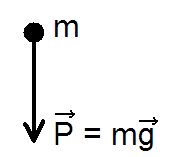
Рис. 10. Сила тяжести – вес

Здесь m – масса точки (в данном случае – футбольного мяча).

Решение задачи. В рассматриваемом случае мы имеем следующие условия, которым должна удовлетворять траектория движения мяча 2

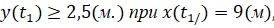    (2)

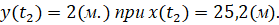    (3)

В (2) t1 – момент времени, соответствующий пролёту мяча над стенкой и в (3) t2 – момент времени, соответствующий пролёту мяча плоскости ворот в заданной точке. Очевидно, что t1 < t2 и для определения этих моментов времени согласно (1) нам потребуется величина начальной скорости 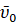полета мяча и уголь ее наклона к горизонту (рис. 8). Зададимся более менее реальной величиной угла и найдем из (1) величину начальной скорости 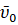, при которой будут выполнены основные условия (3), определяющие попадание мяча в середину левой девятки ворот , а затем проверим на какой высоте в таком случае пролетит мяч над стенкой (рис. 7). Согласно (1) и (3) имеем

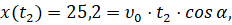
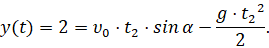    (4)

Из первого условия в (4) выражаем величину вектора начальной скорости

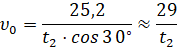
и, подставляя её во второе условие в (4), получаем

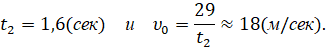    (5)

Теперь сосчитаем, на какой высоте при этих данных пролетит мяч над стенкой. Имеем из условий (2)

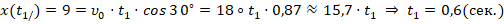
Тогда из (1) получаем

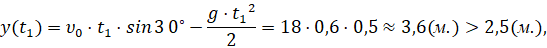
т.е. мяч с запасом пролетает над стенкой. При этом расстояние до стенки в 9 метров он летит примерно 0,6 секунды и остальные примерно 16 метров до центра левой девятки в плоскости ворот (рис. 6) – примерно 1 секунду.

Заключение. Как видим данная математическая модель планирующего полета мяча по вертикальной параболе в девятку ворот со штрафного удара (из-за пределов штрафной площадки) с выстроенной из игроков противника стенкой на расстоянии 9 метров от места выполнения штрафного удара вполне адекватна. Её, конечно, можно совершенствовать, добиваясь оптимальных (по тому или иному разумному критерию [6]) начальной скорости и угла вылета мяча при заданном его начальном положении – точки на футбольном поле, из которой производится штрафной улар, при наличии выстроенной стенки. Такая конструкция вряд ли применима на практике, но может быть использована при моделировании на ЭВМ различных ситуаций выполнения штрафного удара.