Введение. В работе приводится алгоритм управления дроном-квадрокоптером определенного типа для полёта да цели и обратно за фиксированное время. Весь полёт разбивается на фазы – подъём из «гнезда» - места дислокации квадрокоптера и зарядки его аккумуляторной батареи, горизонтальный полет до заданной цели, зависание над целью, горизонтальный полет до горизонтальной координаты гнезда, спуск и посадка в гнездо. Обосновывается некоторый гарантированный способ посадки квадрокоптера в гнездо. Динамическая помеха (ветер) считается детерминированной. Оптимизация процесса проводится по критерию качества, задаваемого в виде интеграла от квадрата реализации управляемого воздействия. Такой критерий качества определяет затраты энергии двигателя «малой тяги», каковыми являются двигатели квадрокоптера, приводящие в движение его вертолетные винты. Используется математическая модель управляемого полёта дрона, разработанная при участии автора [1-3].
Математическая модель. Рассматривается конкретный тип квадрокоптера (рис. 1):

Рис. 1. Квадрокоптер
Данный квадрокоптер может совершать движения по вертикали (взлёт, посадка) и в горизонтальной плоскости. Для указанного типа квадрокоптера время полёта определяется ёмкостью аккумуляторной батареи, обеспечивающей вращение винтов, которые являются управляющими воздействиями для осуществления заданной траектории движения.
Расчетная схема управляемого движения указанного квадрокоптера, согласно [1-3, 9] имеет вид (рис. 2):
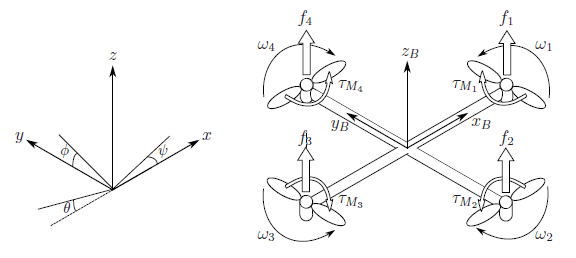
Рис. 2. Расчетная схема квадрокоптера
Согласно [3, 9] математическая управляемая динамическая модель движения квадрокоптера имеет вид:
x=Ax + Bu + Cv + Dg,
tнач ≤ t≤ tкон, (1)
где x – шестимерный вектор:
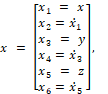
где, в соответствии с общепринятым, точка над буквой обозначает производную по времени t.
В (1) управление u – трёхмерный вектор в декартовой системе координат {x,y,z}:
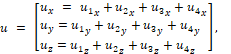
v – вектор помехи (ветер)
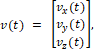
g – ускорение силы тяжести, v – помеха – сила ветра, А, В, С, D – матрицы вид:
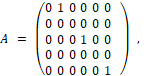


Здесь матрица В выбирается постоянной, т.е. мы полагаем углы Эйлера ϕ,ψ,θ (рис. 2) постоянными и заданными для рассматриваемого полёта. В инерциальной системе отсчета, центробежная сила обнуляется. Таким образом, только гравитационная сила G = mg, величина и направление сил тяги u и помеха v (ветер) участвуют в ускорении квадрокоптера.
Задача. Будем рассматривать случай, когда помеха v (ветер) является постоянной во всё время полёта:
tн=tнач ≤ t ≤ tк=tкон,
где tн и tк заданы и зафиксированы. Содержательно они определяются временным ресурсом полёта квадрокоптера, который определяется, например, для рассматриваемого квадрокоптера (рис. 1) ёмкостью аккумулятора. Так как время полета достаточно мало (например, у указанного типа квадрокоптера оно составляет порядка 10 минут – время полной разрядки аккумулятора) можно, с достаточной степенью вероятности, предположить, что помеха – будет постоянной и детерминированной.
Рассмотрим следующую конкретную задачу. Из состояния покоя в начальный момент времени tн (рис. 3) квадрокоптер стартует и поднимается на заданную высоту h за заданное время tн ≤ t ≤ t1. После этого всё дальнейшее движение квадрокоптера до цели происходит в горизонтальной плоскости. Конструируется программное [4, 5] управление {u(t), t1 ≤ t ≤ t2}, обеспечивающее его подлёт до заданной цели. После этого квадрокоптер зависает над целью на время t2 ≤ t ≤ t3, например, для осуществления, видеосъёмки и возвращается назад за время t3 ≤ t ≤ t4, также совершая горизонтальный полёт на той же высоте h. Выйдя на вертикальную ось, перпендикулярную гнезду, осуществляется спуск и его посадка в «гнездо» за время t4 ≤ t ≤ t5 (рис. 3).
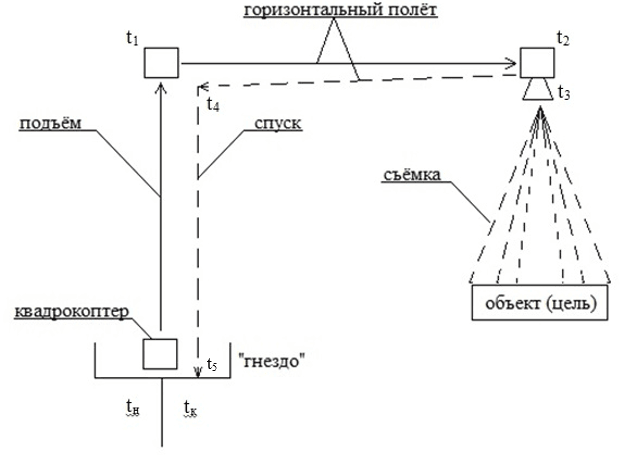
Рис. 3. Схема полёта квадрокоптера до цели и обратно
На каждом этапе полёта квадрокоптеру для осуществления маневра отпускается определенное время, так что tк-tн=t1+(t2-t1)+
(t3-t2)+(t4-t3)+(t5-t4). Как было указано выше суммарное время полёта зафиксировано. При этом обычно полагается tн (3) = 0. Таким образом, здесь возникают естественные ограничения на расстоянии до цели, так как ресурс управляющих воздействий (подъёмных сил винтов) является ограниченным и определяется также энергоёмкостью аккумулятора.
В связи с этим возникает задача о построении такого управления, которое на каждом интервале полёта обеспечивает его оптимальность, т.е. минимум затрат энергии на выработку управляющих воздействий, обеспечивающих решение поставленной задачи.
Известно, что для двигателей малой тяги критерий качества процесса управления [5, 8] для решения такой задачи имеет вид:
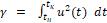 (2)
(2)
Алгоритм оптимального управления. В соответствии с теорией оптимального управления [5, 8], разработанной в Свердловской (ныне Екатеринбургской) школе по оптимальному управлению Н.Н. Красовского, управляющие воздействия сконструируем следующим образом.
На первом этапе подъёма квадрокоптера на заданную высоту h за заданное время tн ≤ t ≤ t1, будем использовать следующие начальные и конечные условия:
tн, x(tн) = xн,x5(t1) = h, ϕ = ϕ*, ψ = ψ*, ϑ = ϑ*,
где h – высота подъёма квадрокоптера. Естественно, предполагается, что эта высота больше высоты цели. Будем полагать, что tн=0 и xн=0, где x – вектор (2). Тогда вектор x(t1) (2) имеет все компоненты равными нулю, кроме компоненты x5=h. При этом на рис. 3 условно траектория подъёма квадрокоптера изображена в виде вертикальной прямой, но благодаря помехе (ветру) она может иметь и криволинейную форму.
Относительно помехи (силы ветра) предполагаем, что на всём отрезке времени полёта (3) она остаётся постоянной v(t)=v*=const и неизменной. Более того, предполагаем, что сила ветра расположена в горизонтальной плоскости, что соответствует реальным условиям полёта квадрокоптера.
Согласно [4, 5] оптимальное по критерию качества (2) управляющие воздействия (программное управление) имеет вид:
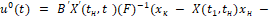

tн ≤ t ≤ t1,
где
 фундаментальная матрица [5] решений однородного дифференциального уравнения:
фундаментальная матрица [5] решений однородного дифференциального уравнения:
x=Ax.
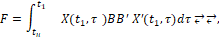
где верхний индекс штрих означает транспонирование.
На втором этапе горизонтального полёта до цели (рис. 3) решается задача о переводе квадрокоптера из точки над «гнездом» в точку над целью. Граничные условия имеют следующий вид:
t1, x(t1), t2,x(t2), v(t) = v*, ϕ = ϕ*, ψ = ψ*, ϑ = ϑ*.
В соответствии с вышеизложенным, оптимальное управление по критерию качества (2), решающее эту задачу, имеет вид:
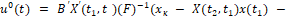

t1 ≤ t ≤ t2.
На третьем этапе решается задача о зависании квадрокоптера над объектом (целью) (рис. 3) на отрезке времени t2 ≤ t ≤ t3, при этом граничные условия имеют вид:
t2, x(t2), t3, x(t3) = x(t2), v(t) = v*, ϕ=ϕ*, ψ = ψ*, ϑ = ϑ*.
Управление, решающее эту задачу, имеет вид:
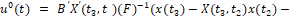

t2 ≤ t ≤ t3.
На четвёртом этапе решается задача об управлении, обеспечивающем полёт квадрокоптера от цели в точку, лежащую на вертикали, перпендикулярную плоскости «гнезда». При этом предполагается, что квадрокоптер некоторое время зависает над целью, например для видеосъёмки. Тогда перелёт на этом этапе начинается в момент времени t3 и заканчивается в момент времени t4 (рис. 3). При этом граничные условия для решения задачи управления имеют следующий вид:
t3, x(t3), t4, x(t4) = x(t1), v(t) = v*, ϕ=ϕ*, ψ = ψ*, ϑ = ϑ*.
Управление, решающее эту задачу, имеет вид:
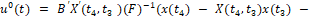

t3 ≤ t ≤ t4.
На последнем пятом этапе, на отрезке времени t4 ≤ t ≤ t5, квадрокоптер спускается в «гнездо». В этом случае граничные условия имеют вид:
t4, x(t4), t5, x(t5) = xн,v(t) = v*, ϕ=ϕ*, ψ = ψ*, ϑ = ϑ*.
Управление, решающее эту задачу, имеет вид:
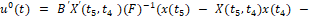
t4 ≤ t ≤ t5.
Итак, мы построили программное управление, складывающееся из пяти управлений (3) и т.д., решающих соответствующие задачи. Известно [4, 5], что так построенное управление на каждом отрезке времени tj ≤ t ≤ tj+1, j=0,...,4, t0=tн (рис. 3) является оптимальным по рассматриваемому критерию качества:

характеризующим затраты энергии на выработку управляющих воздействий.
Хотя работа носит теоретический характер, предлагается способ посадки квадрокоптера в «гнездо», позаимствованный из космической отрасли, а именно стыковки космических аппаратов [7]. Условно схема такой посадки изображена на рис. 4.
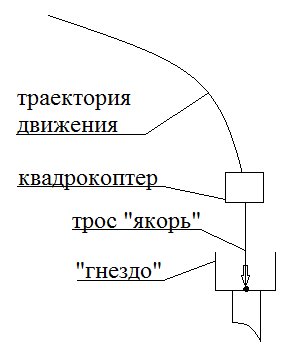
Рис. 4. Гарантированная посадка квадрокоптера в «гнездо»
Попадание квадрокоптера для зарядки – посадка в «гнездо», представляет определённую трудность, в связи с необходимостью большой точности приземления. Хотя квадрокоптер снабжен видеокамерами, это не упрощает решение такой задачи. Известно [7], что при стыковке двух космических аппаратов используется трос, который их соединяет и движение происходит благодаря втягиванию троса в один из аппаратов. Это обеспечивает абсолютную точность стыковки. Можно трактовать трос, как некоторый «якорь» или «гарпун», который выбрасывает один из объектов (стыкующийся) и попадает в стыковочное отверстие второго аппарата. Это используется автором статьи для обоснования возможности решения рассматриваемой задачи на практике.

.png&w=640&q=75)