Совсем недавно, отвечая на вопрос, заданный мне преподавателем: «Почему низкочастотный звук распространяется лучше высокочастотного?», я столкнулся с одним интересным рассуждением. Почему низкочастотный звук распространяется лучше, объясняется легко. Для уверенности в своих мыслях я решил почитать несколько статей на тему звука и наткнулся на одно интересное рассуждение. Оно звучит так: «Принято считать, что человек слышит звук в частотном диапазоне». Но на самом деле нет. Человек воспринимает звук в амплитудном диапазоне, и мы не слышим высокочастотные звуки, так как амплитуда у этих звуков очень мала. Напрашивается вывод, что с повышением частоты, уменьшается амплитуда, а, следовательно, и громкость звука». Когда я прочитал это рассуждение, то понял, что всё так и есть! Представьте, перед вами пианино:
Рис. 1
Нажав на клавишу 1, вы услышите низкий звук, и он будет громким. Но, если вы нажмёте на клавишу 2, а это та же нота, что и клавиша один (до), то вы услышите высокий звук и, он будет значительно тише. Так почему именно так, с этим и попробуем разобраться в этой статье.
Дело в том, что не было никакого объяснения этому явлению в статье, где я об этом прочитал, и не было никакого математического описания, формулы, которая бы показывала, что да, действительно, с увеличением частоты, уменьшается амплитуда. То есть это рассуждение мы должны просто принять на веру. Но я так не смог и решил в этом разобраться. Попытался найти объяснение в интернете, найти формулу, но ничего не вышло, я нигде не смог найти чёткого доказательства данного рассуждения. Тогда я пошёл другим путём, оперируя уже давно всем известными формулами и понятиями, я смог вывести формулу, которая чётко доказывает данное рассуждение.
Сейчас я вам всё продемонстрирую.
Прежде чем перейти к выводу формулы, давайте начнём с азов. Что такое звук?
Звук – это физическое явление, которое представляет собой распространение механических колебаний в виде упругой волны [1, c. 127].
Звуковая волна – волна, которую воспринимает человеческое ухо [1, c. 129].
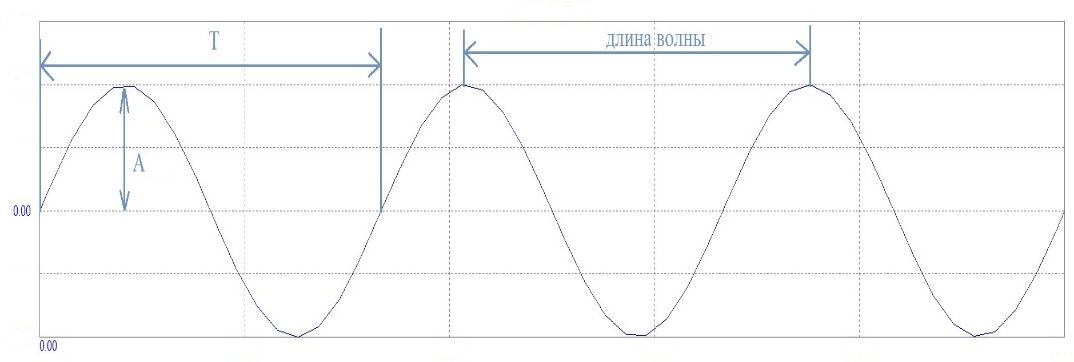
Рис. 2. Звуковая волна
Как и любая другая волна, звуковая волна характеризуется такими параметрами, как: А – амплитуда, Т – период, λ – длина волны, ω – циклическая частота, f – линейная частота, φ – фаза, а также ещё I – интенсивность.
Теперь пробежимся по всем параметрам волны.
Амплитуда – это максимальное отклонение от равновесного состояния [1, c. 104].
Период – это время, за которое совершается одно полное колебание.
Длина волны – это расстояние, на которое распространяется волна за время, равное периоду колебаний [1, c. 125].
Циклическая частота (также называется круговой или угловой частотой) – это частота вращательного или колебательного движения. То есть, эта частота показывает, какое количество частиц совершит колебание за полный цикл и за время Т. Полный цикл это 360°, так как π это 180°, то полный цикл это 2π.
Линейная частота – число полных колебаний за время t.
Фаза – величина, которая определяет состояние колебательной системы в любой момент времени.
Интенсивность – это энергия, проходящая через поверхность единичной площади за промежуток времени ∆t.
Теперь напишем несколько формул для перечисленных параметров.
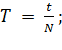(1)
где N – количество колебаний, совершаемых за время t. Период, как и время, измеряется в секундах.
λ = v⋅T; (2)
где v – скорость, с которой распространяется волна.
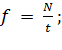(3)
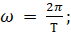(4)
Сделаем некоторые преобразования.
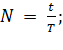из (1), подставим в (3) и получим:
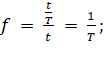(5)
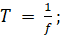(6)
Подставим (6) в (4) и получим:
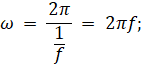
Таким образом, связь между линейной и циклической частотой определяется следующим выражением:
ω = 2πf; (7)
С учётом (6), можем получить следующее выражение для длины волны:
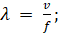(8)
Теперь для того, чтобы ответить на вопрос, почему амплитуда уменьшается с увеличением частоты, нужно разобраться в природе звуковой волны. Звуковая волна, как и любая другая, является переносчиком энергии. Как мы с вами уже разобрались, звуковая волна – это есть не что иное, как колебательный процесс. Любое пространство заполнено мельчайшими частицами, которые, так или иначе, находятся в равновесном состоянии. Воздействуя, каким-либо способом на эти частицы, мы отклоняем их от состояния равновесия, возникают механические колебания. Множество частиц колеблются, образуя тем самым волну. Каждая частица колеблется по гармоническому закону и характеризуется амплитудой и скоростью, с которой частицы перемещаются в пространстве. Колебания частиц описываются следующим законом:
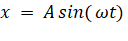или 
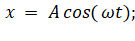(9)
то есть это синус или косинус. А и ω вы уже знаете, а x – это смещение частицы от положения равновесия в данный момент времени.
Скорость, с которой частицы перемещаются в пространстве, это есть производная от перемещения.
v = x';
v = [Acos(ωt)]';
v = -Aωsin(ωt); (10)
Максимальное значение скорости равно:
vmax = -Aω; (11)
Как было сказано ранее, волна – это переносчик энергии. Следовательно, каждая частица обладает энергией. При гармонических колебаниях, каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно. В момент равновесного состояния, потенциальная энергия равна нулю, кинетическая максимальна:
Wп = 0;
Wк = max.
При максимальном отклонении от положения равновесия, всё наоборот:
Wп = max;
Wк = 0.
Рассмотрим на примере кинетической энергии.
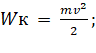(12)
С учётом (11):
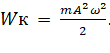(13)
Обозначим энергию одной частицы следующим образом:
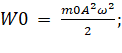(14)
где m0 – масса одной частицы.
W0 – такой энергией обладает одна частица в волне. Чтобы узнать, какую энергию переносит вся волна, необходимо знать количество частиц в волне.
Тогда получим:
Wволны = NW0;
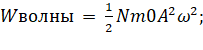(15)
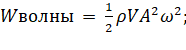(16)
где m = Nm0, а m = ρV, где ρ – плотность, V – объём.
Далее для того, чтобы перейти к понятию интенсивности, о котором мы говорили в самом начале, нужно получить ещё одно выражение. Представим себе две области пространства, в первой - в момент времени t = 0 уже возбуждён колебательный процесс, а во второй области пока всё спокойно. Но в момент времени t = τ колебательный процесс возбудился и там. Графически это будет выглядеть следующим образом:
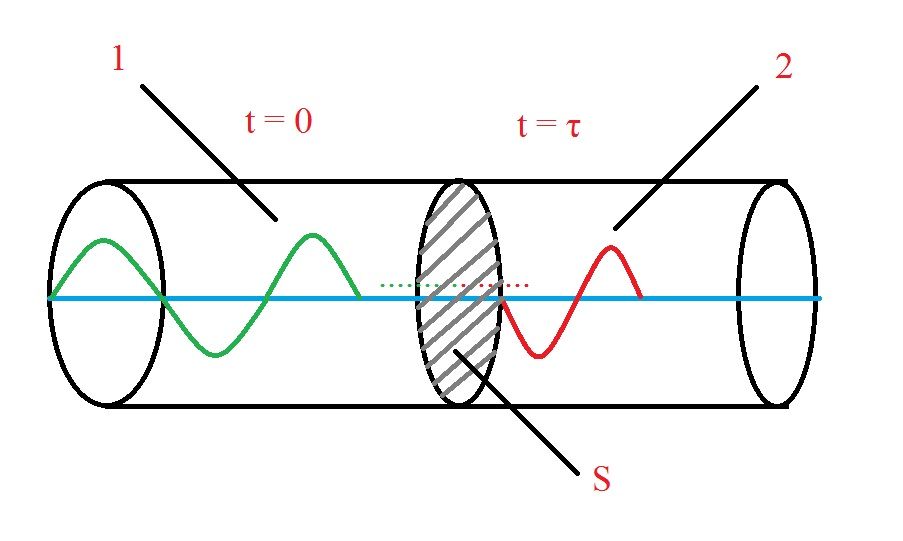
Рис. 3
В итоге, волна распространяется с течением времени и переносит свою энергию в пространстве. Разумно предположить, что волна в пространстве переносит энергию, проходя через некую поверхность площадью S. Также мы можем определить путь, пройденный волной за время t = 0 до t = τ, этот путь, есть не что иное, как длина волны.
λ = v⋅τ. (17)
Тогда объём второй области мы определим, как:
V = S⋅λ = S⋅v⋅τ. (18)
Большое V – это объём, маленькое v – это скорость. С учётом (18) энергия волны будет равна:
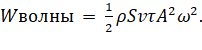(19)
Вернёмся к определению интенсивности.
Интенсивность – это энергия, проходящая через поверхность единичной площади за промежуток времени ∆t.
В виде формулы это запишется следующим образом:
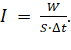(20)
То есть интенсивность звуковой волны характеризует ту часть энергии, которая переносится через поверхность площадью S за промежуток времени ∆t. В нашем случае это промежуток от t = 0 до t = τ, то есть ∆t = τ.
С учётом всего выше сказанного, получим следующее выражение:
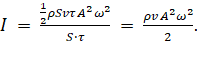(21)
Теперь выражаем амплитуду:
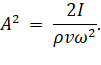
ω = 2πf;
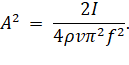
И наконец, окончательная формула:
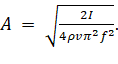(22)
Из формулы (22) мы чётко видим, что при увеличении частоты, амплитуда уменьшается, что и требовалось доказать. Скорость распространения звука в среде это есть v и в нормальных условиях она равна 331 м/с.
.png&w=640&q=75)
